Å fullføre kvadratet

Hva er et fullstendig kvadrat?

Et andregradsutrykk er et fullstendig kvadrat hvis det kan skrives på formen ${\left(x+d\right)}^2$ for et eller annet tall $d$.

Eksempel 1

Ved å bruke

Første kvadratsetning

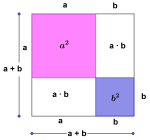
Første kvadratsetning sier at

 ${(a+b)}^2=a^2+2ab+b^2$.

 

første kvadratsetning

$x^2+6x+9={\left(x+3\right)}^2$

$x^2+6x+9$ et fullstendig kvadrat.

Eksempel 2

Er $x^2+6x+9$ et fullstendig kvadrat?

Vi bruker regel 1. Her er $b=6$ og $c=9$, og vi må sjekke om $c={\left(\frac{b}{2}\right)}^2$.

Vi setter inn for $b$ og $c$, og får

$9={\left(\frac{6}{2}\right)}^2$ 

som stemmer. Vi har et fullstendig kvadrat:

${\left(x+\frac{6}{2}\right)}^2={\left(x+3\right)}^2$.

Eksempel 3

Er $x^2+3x-1$ et fullstendig kvadrat?

Vi bruker regel 1. Her er $b=3$ og $c=-1$, og vi må sjekke om $c={\left(\frac{b}{2}\right)}^2$.

Vi setter inn for  og , og får

$-1\ne {\left(\frac{3}{2}\right)}^2=\frac{9}{4}$

som viser at vi ikke har et fullstendig kvadrat.

Å fullføre kvadratet

Vi vil nå ha en metode for å skrive om utrykket $x^2+bx+c$ slik at det likner mest mulig på et fullstendig kvadrat, altså få et utrykk $a{x}^2+bx+c$ på formen ${\left(\cdot \cdot \cdot \right)}^2+r$ der $r$ er en konstant. Vi skal her se på en spesialvariant der konstantleddet $c$  er null. 

Bevis

$x^2+bx=x^2+2\cdot \frac{b}{2}x$

Vi legger så til og trekker fra ${\left(\frac{b}{2}\right)}^2$ (som til sammen blir null og ikke endrer verdien til utrykket),

$=x^2+2\cdot \frac{b}{2}x{+\left(\frac{b}{2}\right)}^2-{\left(\frac{b}{2}\right)}^2$

tilslutt bruker vi

Første kvadratsetning

Første kvadratsetning sier at

 ${(a+b)}^2=a^2+2ab+b^2$.

 

første kvadratsetning

på $x^2+2\cdot \frac{b}{2}x+{\left(\frac{b}{2}\right)}^2={\left(x+\frac{b}{2}\right)}^2$ og får:

$={\left(x+\frac{b}{2}\right)}^2-{\left(\frac{b}{2}\right)}^2$.

Nå har vi bevist regelen over.

Eksempel 4

For å fullføre kvadratet i utrykket $x^2+6x$ bruker vi regel 2 direkte:

$x^2+6x={\left(x+\frac{6}{2}x\right)}^2-\frac{6}{2}={\left(x+3\right)}^2-3$.

Eksempel 5

For å fullføre kvadratet i utrykket $2x^2+6x$ legger vi merke til at det i utrykket står ${2x}^2$ istedet for bare $x^2$ slik det er i regel 2. Derfor begynner vi med å faktorisere (trekke ut $2$):

$2x^2+6x=2\left(x^2+3x\right)$

Vi bruker regel 2 på uttrykket i parentesen:

$x^2+3x=x^2+2\cdot \frac{3}{2}x={\left(x+\frac{3}{2}\right)}^2-{\left(\frac{3}{2}\right)}^2$

Vi går tilbake til det faktoriserte uttrykket og erstatter innholdet i parentesen:

$2\left(x^2+3x\right)=2\left({\left(x+\frac{3}{2}\right)}^2-{\left(\frac{3}{2}\right)}^2\right)=2{\left(x+\frac{3}{2}\right)}^2-2\cdot \frac{9}{4}=2{\left(x+\frac{3}{2}\right)}^2-\frac{9}{2}$.

Eksempel 6

For å fullføre kvadratet i utrykket $x^2-10x-20$ bruker vi regel 2 på første del av utrykket og lar konstanten $-20$ stå:

$x^2-10x-20=x^2-2\cdot 5x-20={\left(x-5\right)}^2-5^2-20$ 

nå har vi bare igjen å legge sammen konstantene: ${\left(x-5\right)}^2-45$.