Retningsvektor
En vektor som er parallell med en rett linje kalles en retningsvektor til linja. Siden vektorene alle er parallelle med (vi har bare forkortet, forlenget eller fått motsatt retning), vil en linje ha uendelig mange retningsvektorer. Det betyr at vi kun trenger å finne én retningsvektor, siden vi får alle de andre ved å multiplisere denne med passende tall.
For å finne en retningsvektor til en rett linje kan vi bruke stigningstallet til linja: En linje som er gitt ved likningen har stigningstall , som betyr at forskjellen i verdiene til to punkter på linja er når forskjellen i verdiene til de samme punktene er . Dermed er en naturlig retningsvektor til linja gitt ved vektoren .
Eksempel 1
En retningsvektor til linja er . Alle vektorer er parallelle med linja.
Retningsvektorene kan brukes til å skrive en rett linje på vektorform.
en rett linje på vektorform
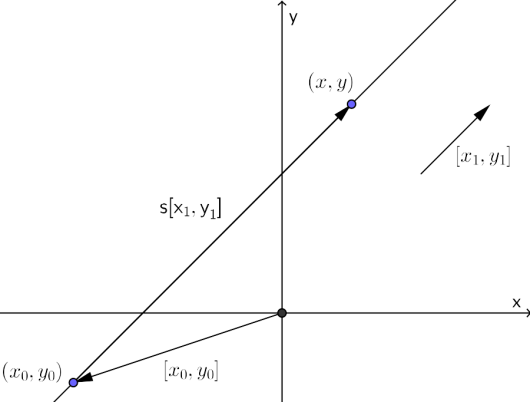
Punktene på en rett linje kan skrives på vektorform som
der er et punkt på linja og er en retningsvektor til linja.
Her er en tegning som forklarer dette (prøv å forklare høyt for deg selv):
Hvordan finner vi vektorformen til en rett linje?
- Hvis vi har gitt linja på formen kan vi for eksempel bruke retningsvektoren i definisjonen over og punktet .
- Hvis vi har gitt to punkter som linja går gjennom, kan vi regne ut stigningstallet , bruke som retningsvektor og et av punktetne for å finne vektorformen.
Eksempel 2
Linja gitt ved har retningsvektor . Av punkter kan vi sette inn ulike verdier for og velge oss et punkt. Vi velger , og får vektorformen .
Når vi har skrevet en linje på vektorform får vi automatisk en såkalt parameterfremstilling av linja, der kalles en parameter. Vektorformen
gir
ved vektoraddisjon og multiplikasjon med . Dermed får vi linja gitt ved likningssystemet
som er det vi kaller en parameterfremstilling for linja.
Eksempel 3
Linja kan skrives på vektorform som , det vil si en mulig parameterfremstilling for linja er
Hadde vi for eksempel valgt punktet isteden, hadde vi fått en mulig parameterfremstilling (vi kaller nå parameteren for )
Ved å sette inn ulike verdier for (som jo kan være hva som helst), får vi de samme punktene, det vil si den samme linja. For eksempel gir punktet , mens også gir .
Legg merke til at siden parameteren kan ta hvilken som helst verdi, har en linje uendelig mange parameterfremstillinger. Vi har her gitt en spesiell metode for å finne slike fremstillinger, ved å bruke retningsvektoren der er stigningstallet til linja.
Del på Facebook
Lynkurs 11.-13.trinn
Vektorer
Består av:
- Hva er en vektor?
- Like vektorer
- Vektorer mellom to punkter
- Vektorer i tre eller flere dimensjoner
- Nullvektor
- Stedvektor (posisjonsvektor)
- Parallelle vektorer
- Lengden til en vektor
- Addisjon av vektorer
- Subtraksjon av vektorer
- Skalarmultiplikasjon
- Prikkprodukt og norm
- Vinkelen mellom to vektorer
- Ortogonale vektorer
- Enhetsvektor og normalisering
- Projeksjon
- Kort om matriser og determinanter
- Kryssprodukt av to vektorer
- Retningsvektor
- Parameterframstilling av en rett linje
- Parametriserte kurver
- Likning til et plan
- Avstand mellom et punkt og et plan
- Likning for en kule
- Kryssprodukt - areal og volum
- Vektorregning med eksempler