Øvingsoppgaver med fasit
Lenke til dette oppgavesettet (kan bokmerkes)Oppgaver
1
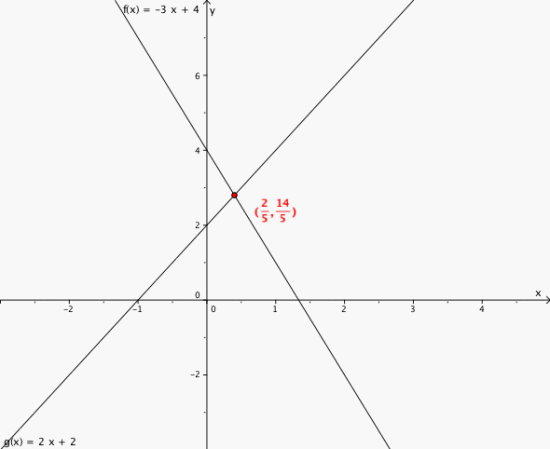
Løs ligningssystemet grafisk:
2
Vi har ulikheten
.
a) Løs ulikheten ved regning.
b) Løs ulikheten grafisk.
3
La være funksjonen
.
a) Finn verdiene og .
b) Tegn grafen for .
c) Finn grafisk når .
4
Funksjonen er gitt ved .
a) Finn toppunktet ved regning.
b) Finn nullpunktene og skjæringspunktet med -aksen.
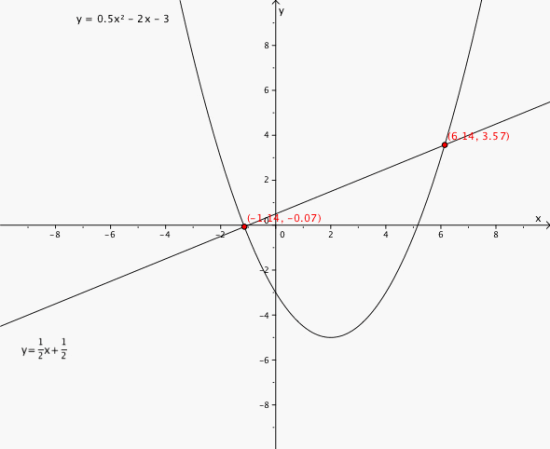
c) Finn skjæringspunktene til med funksjonen ved regning.
d) Hva er symmetriaksene til og ?
5
Undersøk grafisk om ligningssystemet har løsning.
6
Finn eventuelle skjæringspunkter mellom grafen og aksene.
7
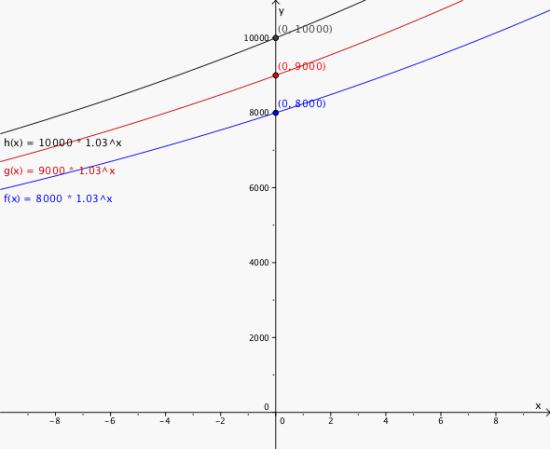
Eksponentialfunksjonene f, g og h er gitt ved:
a) Tegn grafene til f, g og h i samme koordinatysstem.
b) Finn skjæringspunktet med andreaksen for hver av grafene ovenfor. Hva oppdager du? Forklar.
8
La være den rasjonale funksjonen
.
a) Forkort det rasjonale uttrykket.
b) La . Hva er skjæringspunktene mellom og ? Finn -koordinatene ved regning.
9
Det er alltid to skjæringspunkter mellom en rett linje og en andregradsfunksjon. Er denne påstanden riktig? Begrunn svaret.
10
Tegn grafene til f og g i samme koordinatsystem. Vi har gitt at og . Løs ligningen både grafisk og algebraisk.
Fasit
1
To løsninger:
2
a)
b)
3
a) og .
b) og c)
4
a)
b) Nullpunkter: , skjæringspunkt:
c)
d) For og for
5
6
(0,0)
7
a)
b)
8
a)
b)
9
Nei, et moteksempel er
10

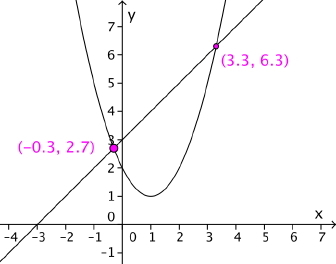
![Figuren viser den grafiske løsningen av ulikheten. Ulikheten er oppfylt for x i intervallet [-3,1].](/aim/matematikk/files/b/0/0/378c539c08094035a9c22ce1377d9518d2387c34ec/b00378c539c08094035a9c22ce1377d9518d2387c34ec.gif/Scale?geometry=360x600>)
![Figuren viser grafen til f(x) for x i intervallet [0,10]. Likningen f(x)=10 er løst grafisk.](/aim/matematikk/files/7/6/f/55cebeb8e2c56e8b796f3642b5419518d2388708ad/76f55cebeb8e2c56e8b796f3642b5419518d2388708ad.gif/Scale?geometry=360x600>)