Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.

Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.

Våre samarbeidspartnere:

REA3024 2014 Vår

Del 1
Del 2
Eksamensinformasjon

Eksamenstid:
5 timer:
Del 1 skal leveres inn etter 2 timer.
Del 2 skal leveres inn senest etter 5 timer.

Hjelpemidler:

Del 1:
Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler

Del 2:
Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.

Framgangsmåte:
Du skal svare på alle oppgavene i Del 1 og Del 2.

Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte.

Om oppgaven krever en bestemt løsningsmetode, vil også en alternativ metode kunne gi noe uttelling.

Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du

viser regneferdigheter og matematisk forståelse
gjennomfører logiske resonnementer
ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
kan bruke hensiktsmessige hjelpemidler
vurderer om svar er rimelige
forklarer framgangsmåter og begrunner svar
skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger

Andre opplysninger:
Kilder for bilder, tegninger osv.

Alle grafer og figurer: Utdanningsdirektoratet
CSI, sodahead.com (28.02.2014)

DEL 1 Uten hjelpemidler

Oppgave 1 (3 poeng) Nettkode: E-4DG6

Deriver funksjonene

a)

$f (x) = \sin (3 x)$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi skal derivere en sinusfunksjon evaluert i $3 x$ . Siden vi vet hvordan vi deriverer $\sin x$ og $3 x$ hver for seg kan det være lurt å benytte kjerneregelen.

Kjerneregelen konstaterer at $(h (g (x)))' = g' (x) h' (g (x))$ . Ved å sette $g (x) = 3 x$ , og merke oss at vi da må ha $h (g) = \sin g$ og derfor $h' (g) = (\sin g)' = \cos g$ og $g' (x) = 3$ , finner vi

$\begin{matrix} f' (x) = g' (x) h' (g (x)) = 3 \cos (g (x)) . \end{matrix}$

Nå har funksjonen $g (x) = 3 x$ utspilt sin rolle som hjelpefunksjon i derivasjonen. Derfor vil det se bedre ut dersom vi skriver $\begin{matrix} f' (x) = 3 \cos 3 x . \end{matrix}$

Svar: $\begin{matrix} f' (x) = 3 \cos (3 x) . \end{matrix}$

Mer om

Denne oppgaven er om

Sinus

Forholdet mellom lengdene til motstående katet og hypotenus til en spiss vinkel i en rettvinklet trekant.

$\sin (A) = \sin (u) = \frac{{motstående}_{katet}}{hypotenus} = \frac{BC}{AC} = \frac{a}{b}$

sinus

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

For flere forklaringer og eksempler på derivasjon, se artikkelen Derivasjon av trigonometriske funksjoner.

Visste du at

Hvis vi i stedet for å skrive $3 x$ hadde skrevet en generell vinkel, $θ (x)$ , ville den deriverte av $f (x)$ blitt $f' (x) = θ' (x) \cos θ (x)$ . Dersom vi tilfeldigvis allerede kjente $f' (x)$ kunne vi altså bestemt $θ' (x)$ ved

$\begin{matrix} θ' (x) = \frac{f' (x)}{\cos (θ (x))}, \end{matrix}$

selv om vi aldri utførte derivasjonen av $θ$ .

b)

$g (x) = e^{2 x} \cdot \cos x$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

$g (x)$ er et produkt av to funksjoner, $e^{2 x}$ og $\cos x$ , som vi vet hvordan vi skal derivere hver for seg. Derfor kan det være lurt å benytte produkteregelen for derivasjon.

Produktregelen for derivasjon sier at hvis $u$ og $v$ er to deriverbare funksjoner, så er $(u v)' = u' v + u v'$ . Vi kan altså sette $u (x) = e^{2 x}$ og $v (x) = \cos x$ . Vi trenger uttrykk for de deriverte $u' (x)$ og $v' (x)$ . Ved å velge $2 x$ som kjerne ser vi at $\begin{matrix} u' (x) = (e^{2 x})' = (2 x)' e^{2 x} = 2 e^{2 x} . \end{matrix}$ Det eneste som gjenstår nå er å minne om at $v' (x) = (\cos x)' = - \sin x$ og sette alt inn i produktregelen $\begin{matrix} g' (x) = u' (x) v (x) + u (x) v' (x) = 2 e^{2 x} \cos x + e^{2 x} (- \sin x) = e^{2 x} (2 \cos x - \sin x) . \end{matrix}$

Svar: $\begin{matrix} g' (x) = e^{2 x} (2 \cos (x) - \sin (x)) . \end{matrix}$

Mer om

Denne oppgaven er om

Sinus

sinus

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjon

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

For flere forklaringer og eksempler på derivasjon, se artikkelen Derivasjonsregler.

Visste du at

Produktregelen for derivasjon kan utledes ved først å huske at den deriverte av en funksjon er definert ved $Δ f / Δ x = [f (x + Δ x) - f (x)] / Δ x$ , der $Δ x$ går mot å bli uendelig liten, og at $v$ er kontinuerlig siden $v$ er deriverbar kan vi skrive ” $\lim_{Δ x \to 0}$ ”, men la oss for denne gang bare huske at $Δ x$ er uendelig liten. Hvis $f (x) = u (x) v (x)$ står det da at $\begin{matrix} f' (x) = \frac{f (x + Δ x) - f (x)}{Δ x} = \frac{u (x + Δ x) v (x + Δ x) - u (x) v (x)}{Δ x} . \end{matrix}$ Ved å legge til og trekke fra $u (x) v (x + Δ x)$ finner vi $\begin{matrix} f' (x) & = \frac{u (x + Δ x) v (x + Δ x) + u (x) v (x + Δ x) - u (x) v (x + Δ x) - u (x) v (x)}{Δ x} \\ = \frac{[u (x + Δ x) - u (x)] v (x + Δ x) + u (x) [v (x + Δ x) - v (x)]}{Δ x} \\ = \frac{u (x + Δ x) - u (x)}{Δ x} v (x + Δ x) + u (x) \frac{v (x + Δ x) - v (x)}{Δ x} \\ = u' (x) v (x + Δ x) + u (x) v' (x), \end{matrix}$ og siden $Δ x$ er uendelig liten kan vi skrive $f' (x) = u' (x) v (x) + u (x) v' (x)$ .

Oppgave 2 (4 poeng) Nettkode: E-4DG9

Regn ut integralene

a)

$\int_{}^{} 2 x \cdot \sin (x^{2}) dx$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi ønsker å finne en funksjon som har derivert lik $2 x \sin x^{2}$ . Siden $2 x$ er den deriverte til $x^{2}$ kan vi forsøke substitusjonsmetoden med substitusjonen $u = x^{2}$ .

Ved å bruke substitusjonsmetoden, som sier at $\int f (u (x)) u' (x) d x = \int f (u) d u$ , med substitusjonen $u (x) = x^{2}$ finner vi at siden $u' (x) = 2 x$ så kan vi skrive

$\begin{matrix} \int 2 x \cdot \sin (x^{2}) d x = \int u' (x) \cdot \sin u (x) d x = \int \sin u d u . \end{matrix}$

Siden den deriverte av $- \cos x$ er $\sin x$ finner vi videre at

$\begin{matrix} \int \sin u d u = - \cos u + C, \end{matrix}$

der $C$ er en konstant som tar høyde for at konstantledd uansett bortfaller under derivasjonen. Til slutt kan vi uttrykke løsningen ved hjelp av $x$ , slik at vi ikke lenger trenger å huske på definisjonen $u (x) = x^{2}$ . Da får vi $\begin{matrix} \int 2 x \cdot \sin (x^{2}) d x = - \cos x^{2} + C . \end{matrix}$

Svar: $\begin{matrix} \int 2 x \cdot \sin (x^{2}) d x = - \cos (x^{2}) + C . \end{matrix}$

Mer om

Denne oppgaven er om

Sinus

sinus

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

For flere forklaringer og eksempler på integrasjon, se artikkelen Integrasjon ved substitusjon.

b)

$\int_{1}^{e} x \cdot \ln x dx$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi må integrere produktet av funksjonene $x$ og $\ln x$ fra $1$ til $e$ . Siden vi ønsker å unngå å integrere $\ln x$ kan det være lurt å benytte metoden for delvis integrasjon.

Metoden for delvis integrasjon sier at $\int u' v d x = u v - \int u v' d x$ . Hvis vi setter $u' (x) = x$ og $v (x) = \ln x$ finner vi $u (x) = \frac{1}{2} x^{2}$ siden $(\frac{1}{2} x^{2})' = x$ og $v' (x) = (\ln x)' = \frac{1}{x}$ . Altså er

$\begin{matrix} \int_{1}^{e} x \cdot \ln x d x & = \int_{1}^{e} u^{'} v d x = {[u v]}_{1}^{e} - \int_{1}^{e} u v' d x = {[\frac{1}{2} x^{2} \ln x]}_{1}^{e} - \int_{1}^{e} \frac{1}{2} x^{2} \frac{1}{x} d x \\ = {[\frac{1}{2} x^{2} \ln x]}_{1}^{e} - \frac{1}{2} \int_{1}^{e} x d x = {[\frac{1}{2} x^{2} \ln x]}_{1}^{e} - \frac{1}{2} {[\frac{1}{2} x^{2}]}_{1}^{e} \\ = (\frac{1}{2} e^{2} \ln e - \frac{1}{2} \cdot 1^{2} \ln 1) - \frac{1}{2} (\frac{1}{2} e^{2} - \frac{1}{2} \cdot 1^{2}) \\ = \frac{1}{2} e^{2} - \frac{1}{4} e^{2} + \frac{1}{4} = \frac{1}{4} (e^{2} + 1) . \end{matrix}$

Svar: $\begin{matrix} \int_{1}^{e} x \cdot \ln (x) d x = \frac{1}{4} (e^{2} + 1) . \end{matrix}$

Mer om

Denne oppgaven er om

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritme

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

For flere forklaringer og eksempler på integrasjon, se artikkelen Delvis integrasjon.

Oppgave 3 (2 poeng) Nettkode: E-4DGC

Funksjonen $f$ er gitt ved

$f (x) = e^{2 x} - 4 e^{x}, D_{f} = ℝ$

Bestem koordinatene til eventuelle vendepunkter på grafen til $f$ .

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi ser etter punkter der $f ″ (x) = 0$ og bytter fortegn.

Vi begynner med å finne et uttrykk for den dobbelderiverte til $f$ . Ved å bruke kjerneregelen med kjerne $2 x$ , at $e^{x}$ er uendret under derivasjon og at den deriverte av en sum er en sum av deriverte finner vi $\begin{matrix} f' (x) = (2 x)' e^{2 x} - 4 e^{x} = 2 e^{2 x} - 4 e^{x} . \end{matrix}$ Helt tilsvarende finner vi $\begin{matrix} f ″ (x) = 4 e^{2 x} - 4 e^{x} . \end{matrix}$ Et vendepunkt $x$ må tilfredsstille $f ″ (x) = 0$ , som betyr at $\begin{matrix} 4 e^{2 x} - 4 e^{x} = 0 \Rightarrow e^{x} (e^{x} - 1) = 0 . \end{matrix}$ Siden $e^{x}$ aldri kan bli null må $e^{x} - 1 = 0$ . Det betyr at $e^{x} = 1$ som tilfredsstilles av $x = 0$ . For å være sikker på at $x = 0$ faktisk er et vendepunkt er vi nødt til å undersøke om $f ″ (x)$ bytter fortegn i $x = 0$ . For $x < 0$ blir $e^{x} - 1$ negativ, og derfor $f ″ (x)$ negativ, mens for $x > 0$ blir $e^{x} - 1$ positiv, og derfor $f ″ (x)$ positiv.

Altså bytter $f ″ (x)$ fortegn i $x = 0$ . Det betyr at vi har funnet vendepunktets $x$ -koordinat. Siden vendepunktet ligger på grafen til $f$ betyr det at $y$ -koordinaten til vendepunktet er gitt av $f (0) = e^{0} - 4 e^{0} = 1 - 4 = - 3$ . Altså er koordinatene til vendepunktet på grafen til $f$ $\begin{matrix} (0, - 3) . \end{matrix}$

Svar: $\begin{matrix} (0, - 3) . \end{matrix}$

Mer om

Denne oppgaven er om

Vendepunkt

Et vendepunkt for en funksjon $f (x)$ er et punkt $x = a$ , der funksjonen bytter mellom å være konveks og konkav. I et vendepunkt skifter den annenderiverte $f'' (x)$ fortegn.

vendepunkt

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjon

Graf

En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.

graf

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Andrederiverte

Den andrederiverte til en funksjon $f (x)$ er funksjonen derivert to ganger og skrives $f'' (x)$ eller $f^{(2)} (x)$ . Kalles også annenderiverte eller dobbeltderiverte.

annenderivert

For flere forklaringer og eksempler på vendepunkter, se artikkelen Vendepunkt og vendetangent.

Oppgave 4 (4 poeng) Nettkode: E-4DGE

En uendelig geometrisk rekke er gitt ved

$s (x) = 1 + (1 - x) + {(1 - x)}^{2} + {(1 - x)}^{3} + . . .$

a)

Bestem konvergensområdet til rekken.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

$s (x)$ er summen av alle positive heltallseksponenter av $(1 - x)$ . Vi må finne de $x$ -verdiene som gjør at $s (x)$ har en veldefinert verdi ulik uendelig.

Siden en endelig geometrisk rekke $S_{n} = a + a k + a k^{2} + a k^{3} + . . . + a k^{n}$ tilfredsstiller $S_{n} - k S_{n} = S_{n} (1 - k) = a - a k^{n + 1}$ må $\begin{matrix} S_{n} = a \frac{1 - k^{n + 1}}{1 - k} . \end{matrix}$ Hvis vi nå lar rekken bli uendelig stor ser vi at den konvergerer hvis, og bare hvis, $| k | < 1$ . I vår uendelige, geometriske rekke er $a = 1$ og $k = (1 - x)$ . Det betyr at rekken konvergerer for $| 1 - x | < 1$ . Med andre ord må $- 1 < 1 - x < 1$ som betyr at $- 2 < - x < 0$ . Multiplikasjon med $- 1$ gir da $0 < x < 2$ som konvergensområde.

Svar: $\begin{matrix} 0 < x < 2 . \end{matrix}$

Mer om

Denne oppgaven er om

Sum

Resultatet av en addisjon.

Eksempel: 2 + 5 + 1 = 8, her kalles 8 for sum.

sum

Konvergens

Konvergens betyr i matematikk å nærme seg en grense.

Se Konvergent tallfølge

konvergens

Uendelige rekker

En rekke er en sum av elementene i en tallfølge. Rekken kalles uendelig hvis den består av uendelig antall elementer.

Eksempel : $\sum_{n = 1}^{\infty} x_{n}$

( ∞ er tegnet for uendelighet )

uendelig rekke

For flere forklaringer og eksempler på rekker, se artikkelen Geometriske rekker.

Visste du at

I enkelte situasjoner er man nødt til å håndtere rekker som ikke konvergerer. Selv om rekken $s_{1} = 1 - 1 + 1 - 1 + 1 - 1 + . . .$ veksler mellom å være $0$ og $1$ og derfor ikke konvergerer, kan det være fristende å late som om den konvergerer mot gjennomsnittet, nemlig $\frac{1}{2}$ . Vi kan for eksempel tenke på $s$ som en lyspære, som enten kan være på eller av. Dersom man skrur av og på lyset uendelig mange ganger og uendelig fort føles det ikke så urimelig å si at det vil oppfattes som om lyset bare lyser med halv styrke.

Det skjer imidlertid mange rare ting dersom man godtar at $s = 1 - 1 + 1 - 1 + 1 - 1 + . . . = \frac{1}{2}$ . En av disse er det merkelige resultatet $1 + 2 + 3 + 4 + 5 + 6 + . . . = - \frac{1}{12}$ , som sier at summen av alle positive heltall er lik minus én tolvtedel.

b)

Løs likningene

$s (x) = 3$ og $s (x) = \frac{1}{3}$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

For å løse likningene må vi først finne et uttrykk for tallet $s (x)$ konvergerer mot.

Ved enten å huske at en uendelig, konvergent geometrisk rekke $a + a k + a k^{2} + a k^{3} + . . .$ konvergerer mot $\frac{a}{1 - k}$ , eller å følge argumentasjonen i oppgave $4 a)$ og se at hvis $| k | < 1$ må $k^{n + 1}$ gå mot null og derfor $a + a k + a k^{2} + a k^{3} + . . . = \frac{a}{1 - k}$ , finner vi $\begin{matrix} s (x) = \frac{1}{1 - (1 - x)} = \frac{1}{x} . \end{matrix}$ Likningen $s (x) = 3$ er altså ekvivalent med likningen $\frac{1}{x} = 3$ , som løses av $x = \frac{1}{3}$ som er i definisjonsmengden til $s$ . Helt tilsvarende løses likningen $s (x) = \frac{1}{x} = \frac{1}{3}$ av $x = 3$ som ikke er i definisjonsmengden til $s$ . Likningen har da ingen løsning.

Svar: $s (\frac{1}{3}) = 3 og s (3) = \frac{1}{3}$

Mer om

Denne oppgaven er om

Konvergent tallfølge

En tallfølge konvergerer mot et tall k, hvis tallfølgen nærmer seg k som sin grense.

Eksempel: $\frac{1}{1}, \frac{1}{2}, \frac{1}{3}, . . . \frac{1}{i}, . . .$

Denne tallfølgen konvergerer mot 0, fordi tallene i følgen kommer nærmere og nærmere 0.

konvergent følge

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

For flere forklaringer og eksempler på rekker, se artikkelen Konvergente tallfølger.

Oppgave 5 (5 poeng) Nettkode: E-4DGH

Planet $α$ er gitt ved

$α : 2 x + y - 2 z + 3 = 0$

a)

Vis at punktet $P (3, 4, 2)$ ikke ligger i planet $α$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Punktene som ligger i planet $α$ er nøyaktig de punktene som tilfredsstiller likningen til planet. De punktene som ikke ligger i planet $α$ er med andre ord de punktene som ikke tilfredsstiller likningen til planet.

Dersom koordinatene til $P$ , når de settes inn i likningen til planet, ikke respekterer likhetstegnet kan ikke punktet $P$ ligge i planet $α$ . Vi har $\begin{matrix} 2 x_{P} + y_{P} - 2 z_{P} + 3 = 2 \cdot 3 + 4 - 2 \cdot 2 + 3 = 6 + 4 - 4 + 3 = 9 \neq 0, \end{matrix}$ som altså betyr at $P$ ikke ligger i planet $α$ .

Mer om

Denne oppgaven er om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektor

Plan

Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.

plan

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

Punkt

I geometrien tegnes punkt som en prikk eller et kryss. Den knyttes til en fast posisjon og har ingen utstrekning. Et punkt har en stor bokstav som navn, for eksempel A eller B.

punkt

For flere forklaringer og eksempler på vektorer, se artikkelen Likning til et plan.

Visste du at

At likningen for planet $α$ er $2 x + y - 2 z + 3 = 0$ betyr at et punkt $P (x, y, z)$ ligger i planet hvis, og bare hvis, koordinatene til $P$ tilfredsstiller likningen. Vi kan altså skrive $α = {(x, y, z) \in ℝ^{3} | 2 x + y - 2 z + 3 = 0}$ , som leses ” $α$ er mengden av alle punkter $(x, y, z)$ i rommet ( $ℝ^{3}$ ) som tilfredsstiller $2 x + y - 2 z + 3 = 0$ ”.

b)

En linje $l$ går gjennom $P$ slik at $l ⊥ α$ .

Bestem en parameterframstilling for $l$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

For å uttrykke linjen $ℓ$ , som står normalt på planet $α$ og går gjennom $P$ , kan det være lurt å først finne en vektor $\vec{n}$ som står normalt på planet. Parameterfremstillingen av $ℓ$ er da gitt som $\vec{O P} + t \vec{n}$ der $t \in ℝ$ .

At likningen for planet $α$ er $2 x + y - 2 z + 3 = 0$ , kan vi tenke på som kravet om at enhver vektor mellom to punkter i $α$ må stå orthogonalt på en såkalt normalvektor, $\vec{n} = [2, 1, - 2]$ . Fra konstantleddet kan vi lese av avstanden, $d = \frac{3}{|\vec{n}|}$ , planet har fra Origo. Siden normalvektoren $\vec{n}$ står vinkelrett på planet $α$ må $\vec{n}$ være parallell med $ℓ$ . Det betyr at for alle $t \in ℝ$ må $\vec{O P} + t \vec{n}$ ligge i $α$ . Parameterfremstillingen for linjen $ℓ$ er altså

$\begin{matrix} \vec{O P} + t \vec{n} = [3, 4, 2] + t [2, 1, - 2] = [3 + 2 t, 4 + t, 2 - 2 t], \end{matrix}$ eller $\begin{matrix} ℓ : {\begin{matrix} x & = 3 + 2 t \\ y & = 4 + t \\ z & = 2 - 2 t \end{matrix} . \end{matrix}$

Svar:

$l : (3 + t, 4 + t, 2 - 2 t) for t \in ℝ$

eller

$\begin{matrix} ℓ : {\begin{matrix} x & = 3 + 2 t \\ y & = 4 + t \\ z & = 2 - 2 t \end{matrix} . \end{matrix}$

Mer om

Denne oppgaven er om

Linje

En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.

linje

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektor

Normal

En linje som står 90 grader på en annen linje.

normalt

Plan

Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.

plan

For flere forklaringer og eksempler på vektorer, se artikkelen Parameterframstilling av en rett linje.

c)

Bestem koordinatene til skjæringspunktet mellom $l$ og $α$ .

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Skjæringspunktet mellom $ℓ$ og $α$ er nøyaktig de koordinatene i $ℓ$ som tilfredsstiller likningen til planet.

Ved å sette inn koordinatene fra parameterfremstillingen av linjen $ℓ$ inn i likningen til planet kan vi bestemme parameteren $t$ . Det kan vi bruke til å uttrykke koordinatene til skjæringspunktet. Et punkt på linjen $ℓ$ kan skrives $Q (3 + 2 t, 4 + t, 2 - 2 t)$ er en parameter $t \in ℝ$ . Dette punktet ligger i planet $α$ når $\begin{matrix} 2 x_{Q} + y_{Q} - 2 z_{Q} + 3 & = 2 (3 + 2 t) + (4 + t) - 2 (2 - 2 t) + 3 \\ = 6 + 4 t + 4 + t - 4 + 4 t + 3 = 9 t + 9 = 0 . \end{matrix}$ Altså ligger $Q$ i planet $α$ hvis $t = - \frac{9}{9} = - 1$ . Det betyr at skjæringspunktet mellom $ℓ$ og $α$ har koordinatene $\begin{matrix} Q & = (3 + 2 (- 1), 4 + (- 1), 2 - 2 (- 1)) = (1, 3, 4) \end{matrix}$

Svar: $(1, 3, 4)$

Mer om

Denne oppgaven er om

Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.

skjæringspunkt

Linje

En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.

linje

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

Plan

Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.

plan

Punkt

I geometrien tegnes punkt som en prikk eller et kryss. Den knyttes til en fast posisjon og har ingen utstrekning. Et punkt har en stor bokstav som navn, for eksempel A eller B.

punkt

For flere forklaringer og eksempler på vektorer, se artikkelen Parametriserte kurver.

Visste du at

Vi kan uttrykke grafen til enhver funksjon $f (x)$ ved hjelp av en parameterfremstilling. At grafen til $f$ er nøyaktig de punktene i planet med koordinater $(x, f (x))$ for en eller annen $x \in D_{f}$ , er nettopp en parameterfremstilling av grafen til $f$ med $x$ som parameter.

d)

Bestem avstanden fra $P$ til $α$ .

Løs oppgaven her

Løsningsforslag d)

Jeg tenker

Avstanden fra $P$ til $α$ er avstanden, langs $ℓ$ , fra $P$ til skjæringspunktet mellom $ℓ$ og $α$ .

Avstandsformelen konstaterer at avstanden fra et plan $α$ , gitt ved likningen $A x + B y + C z + D = 0$ , til et punkt $P (x_{P}, y_{P}, z_{P})$ er $\begin{matrix} D = \frac{| A x_{P} + B y_{P} + C z_{P} + D |}{\sqrt{A^{2} + B^{2} + C^{2}}} . \end{matrix}$ Det betyr at avstanden fra $P$ til $α$ er gitt som $\begin{matrix} D & = \frac{| 2 x_{P} + y_{P} - 2 z_{P} + 3 |}{\sqrt{2^{2} + 1^{2} + (- 2)^{2}}} = \frac{| 2 \cdot 3 + 4 - 2 \cdot 2 + 3 |}{\sqrt{9}} = \frac{| 9 |}{3} = 3 . \end{matrix}$

Alternative løsninger

Alternativ i)

Dersom $Q$ er skjæringspunktet mellom $ℓ$ og $α$ , og $S$ er skjæringspunktet mellom linjen $O P$ og $α$ er $△ Q S P$ rettvinklet. Det betyr at $\cos ∠ Q P S = Q P / S P$ , der $Q P$ er avstanden fra $P$ til $α$ . Ifølge $\vec{a} \cdot \vec{b} = | a | \cdot | b | \cos θ$ , der $θ$ er vinkelen mellom $\vec{a}$ og $\vec{b}$ , kan vi skrive

$\begin{matrix} Q P & = S P \cdot \cos ∠ Q P S = |\vec{S P}| \cdot |\frac{\vec{n}}{|\vec{n}|}| \cos ∠ Q P S = |\vec{S P} \cdot \frac{\vec{n}}{|\vec{n}|}| \end{matrix}$

Siden $S$ ligger i $α$ impliserer likningen til planet at $\vec{O S} \cdot \vec{n} = - 3$ , som betyr at $\begin{matrix} \vec{S P} \cdot \frac{\vec{n}}{|\vec{n}|} & = (\vec{O P} - \vec{O S}) \cdot \frac{\vec{n}}{|\vec{n}|} = \frac{(\vec{O P} \cdot \vec{n} - (- 3))}{|\vec{n}|} \\ = \frac{([3, 4, 2] \cdot [2, 1, - 2] + 3)}{\sqrt{2^{2} + 1^{2} + (- 2)^{2}}} = \frac{(6 + 4 - 4 + 3)}{\sqrt{9}} = \frac{9}{3} = 3 . \end{matrix}$ Altså er avstanden fra $P$ til $α$ lik $3$ .

Alternativ ii)

La $Q$ være skjæringspunktet mellom $α$ og $ℓ$ . Siden $ℓ$ og $ℓ$ $⊥ α$ , må $P Q ⊥ α$ . Avstanden fra $P$ til $α$ blir derfor lik $|\vec{P Q}|$ . Vi finner $\vec{P Q} = [1 - 3, 3 - 4, 4 - 2] = [- 2, - 1, 2]$ . Det gir $|\vec{P Q}| = \sqrt{{(- 2)}^{2} + {(- 1)}^{2} + 2^{2}} = 3$ .

Svar: Avstanden fra $P$ til $α$ lik $3$ .

Mer om

Denne oppgaven er om

Skjæringspunkt

skjæringspunkt

Linje

En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.

linje

Rett vinkel

En rett vinkel er 90 grader og vi skriver 90°. Vi sier da at vinkelbeina står normalt på hverandre.

rett vinkel

Plan

Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.

plan

Punkt

I geometrien tegnes punkt som en prikk eller et kryss. Den knyttes til en fast posisjon og har ingen utstrekning. Et punkt har en stor bokstav som navn, for eksempel A eller B.

punkt

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

For flere forklaringer og eksempler på vektorer, se artikkelen Avstand mellom et punkt og et plan.

Oppgave 6 (4 poeng) Nettkode: E-4DGM

En funksjon $f$ er gitt ved

$f (x) = a \sin (c x + φ) + d$

Grafen til funksjonen har et toppunkt i $(0, 7)$ . Det nærmeste bunnpunktet til høyre for dette toppunktet er $(2, 3)$ .

a)

Forklar at funksjonsuttrykket kan skrives

$f (x) = 2 \sin (\frac{π}{2} x + \frac{π}{2}) + 5$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi må bruke de to punktene til å bestemme amplituden $a$ , likvektslinjen $d$ , vinkelfrekvensen $c$ og faseleddet $ϕ$ .

Siden gjennomsnittet av topp- og bunnpunktenes $y$ -verdier i en sinusfunksjon er null, må et eventuelt avvik i den samme verdien for $f (x)$ skyldes konstanten $d$ . Vi må med andre ord ha $\begin{matrix} d = \frac{y_{t o p p} + y_{b u n n}}{2} = \frac{7 + 3}{2} = \frac{10}{2} = 5 . \end{matrix}$ Siden en sinusfunksjon aldri kan bli større enn én må forskjellen mellom likevektslinjen $y = 5$ og toppunktets $y$ -verdi $y = 7$ gi amplituden til $f (x)$ . Altså må $\begin{matrix} a = y_{t o p p} - y_{l i k e v e k t} = 7 - 5 = 2 . \end{matrix}$ Videre har vi at vinkelforskjellen mellom topp- og bunnpunkt i en sinusfunksjon er $π$ . Det betyr at vinkelendringen $c Δ x = c (x_{b u n n} - x_{t o p p})$ å være $π$ . Altså $\begin{matrix} c = \frac{π}{x_{b u n n} - x_{t o p p}} = \frac{π}{2} . \end{matrix}$ Til slutt må vi finne verdien av konstanten $ϕ$ , som er skyld i at funksjonen $f (x)$ ikke begynner lik null slik sinus gjør. Siden $c x + ϕ = c (x - (\frac{- ϕ}{c}))$ må $\frac{- ϕ}{c}$ være faseforskyvningen til $f (x)$ . Siden $f (x)$ er faseforskjøvet $\frac{1}{2} (0 + 2) = 1$ til venstre følger det at $\begin{matrix} \frac{- ϕ}{c} = - 1 \Rightarrow ϕ = c = \frac{π}{2} . \end{matrix}$ Altså er $\begin{matrix} f (x) = 2 \sin (\frac{π}{2} x + \frac{π}{2}) + 5 . \end{matrix}$

Mer om

Denne oppgaven er om

Sinus

sinus

Toppunkt

Et toppunkt for en funksjon er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er større enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

toppunkt

Bunnpunkt

Et bunnpunkt for en funksjon $f (x)$ er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er mindre enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

bunnpunkt

Gjennomsnitt

Gjennomsnitt er en middelverdi av alle dataene.

Gjennomsnittet finner du ved å:
1) summere alle data
2) dele summen på total antall data

Eksempel: Gjennomsnittet av 2, 2, 4, 3 er 2,75 fordi
1) $2 + 2 + 4 + 3 = 11$
2) antall data er 4. $11 : 4 = 2, 75$

gjennomsnitt

Pi (π)

$π$ er forholdet mellom sirkelens omkrets og diameter. Dette forholdet er alltid konstant og tilnærmet lik 3,14.

For flere forklaringer og eksempler på trigonometriske funksjoner, se artikkelen Periodiske funksjoner.

Visste du at

Siden vinkelen i sinusfunksjonen som inngår i $f (x)$ er forskjøvet med $90^{\circ}$ kan vi uttrykke sinusfunksjonen som en cosinusfunksjon uten faseforskyvning. Det vil si $\begin{matrix} f (x) = 2 \cos (\frac{π}{2} x) + 5 . \end{matrix}$

b)

Lag en skisse av grafen til $f$ for $x \in [0, 12]$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Siden $f (x)$ er en harmonisk svingning som begynner i et toppunkt i $x = 0$ vil grafen til $f$ se ut som en cosinusfunksjon rundt likvektslinjen $y = 5$ .

Ettersom én periode har lengde $4$ må grafen vise tre hele svingninger. Siden $(0, 7)$ er et toppunkt må vi videre ha bunnpunkt i $(2, 3)$ , toppunkt i $(4, 7)$ , bunnpunkt i $(6, 3)$ , toppunkt i $(8, 7)$ , og så videre. Vi kan altså merke av skjæringspunktene med likevektslinjen $y = 5$ og ekstremalpunktene $\begin{matrix} L i k e v e k t s l i n j e n & = {(1, 5), (3, 5), (5, 5), (7, 5), (9, 5), (11, 5)} \\ T o p p u n k t e r & = {(0, 7), (4, 7), (8, 7), (12, 7)} \\ B u n n p u n k t e r & = {(2, 3), (6, 3), (10, 3)} . \end{matrix}$ Resultatet blir da som følger

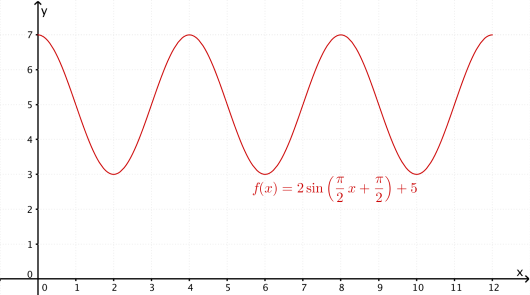
Svar:

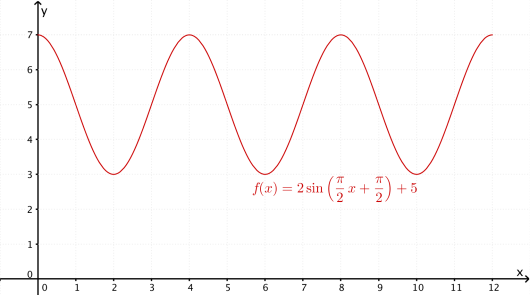
Mer om

Denne oppgaven er om

Ekstremalpunkter

Ekstremalpunkter er en samlebetegnelse på topp- og bunnpunkter.

ekstremalpunkter

Toppvinkler

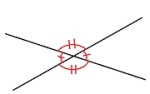
Når to rette linjer skjærer hverandre, dannes to par like store vinkler. Et slikt par kalles toppvinkler.

toppunkt

Bunnpunkt

Et bunnpunkt for en funksjon $f (x)$ er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er mindre enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

bunnpunkt

Graf

graf

Skjæringspunkt

skjæringspunkt

Sinus

sinus

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

For flere forklaringer og eksempler på ekstremalpunkter, se artikkelen Topp- og bunnpunkter.

Visste du at

Lyder er harmoniske svingninger i lufttrykket og kan derfor representeres ved funksjoner av typen $f (x)$ . Dersom dersom én enhet langs $x$ -aksen tilsvarer $1 / 110$ sekund og $y$ -aksen representerer lufttrykket, vil $f (x)$ være en harmonisk svingning i lufttrykket med frekvens $440 H z$ – altså en enstrøken $A$ .

Oppgave 7 (2 poeng) Nettkode: E-4DGP

Løs differensiallikningen

$y' - 3 y = 2$ når $y (0) = \frac{1}{3}$

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi må finne en funksjon $y (x)$ som tilfredsstiller $y' - 3 y = 2$ og som går gjennom punktet $(0, 1 / 3)$ . Siden det ikke er noen eksplisitt $x$ -avhengighet og bare $y$ og dens førstederiverte dukker opp i differensiallikningen over, er likningen en såkalt separabel differensiallikning av første orden.

For å løse likningen $y' - 3 y = 2$ kan det være lurt å gjennomføre omskrivingen $y' = 2 + 3 y$ som videre kan omformuleres til $\begin{matrix} \frac{y'}{2 + 3 y} = 1 . \end{matrix}$ Denne omformingen gjelder så lenge vi ikke får $0$ i nevner på venstre side, altså så lenge $y$ ikke er den konstante funksjonen $y (x) = - \frac{2}{3}$ . Ved innsetting ser vi at $y = - \frac{2}{3}$ gir funksjonen som er konstant lik $0$ på begge sider av den opprinnelige likningen, så dette er en løsning.

Ved å integrere med hensyn på $x$ på begge sider av likhetstegnet sitter vi da igjen med $\begin{matrix} \int \frac{y' (x) d x}{2 + 3 y (x)} = \int \frac{d y}{2 + 3 y} = \int d x \end{matrix}$ ifølge substitusjonsmetoden for integrasjon med substitusjonen $y = y (x)$ . Integralet på høyresiden, $\int d x$ , tar formen $x + C_{1}$ der $C_{1}$ er en vilkårlig konstant siden den deriverte av $x + C_{1}$ er én. Ved å bruke substitusjonen $u (y) = 2 + 3 y$ , med $u' (y) = 3$ , kan vi videre skrive

$\begin{matrix} \int \frac{d y}{2 + 3 y} = \int \frac{\frac{1}{3} u' (y) d y}{u (y)} = \frac{1}{3} \int \frac{d u}{u} = \frac{1}{3} \ln |u| + C_{2} \end{matrix}$

der $C_{2}$ er en vilkårlig konstant. Ved å sette inn for $u$ sitter vi da igjen med at

$\begin{matrix} \frac{1}{3} \ln |u| + C_{2} = \frac{1}{3} \ln |(2 + 3 y)| + C_{2} . \end{matrix}$

Siden både $C_{1}$ og $C_{2}$ er vilkårlige konstanter kan vi like gjerne velge en vilkårlig konstant $C = 3 (C_{1} - C_{2})$ og se at

$\begin{matrix} \frac{1}{3} \ln |(2 + 3 y)| + C_{2} = x + C_{1} \Rightarrow \ln |(2 + 3 y)| = 3 x + C . \end{matrix}$

Ved å bruke eksponentialfunksjonen på begge sider, får vi

$\begin{matrix} \Rightarrow & |2 + 3 y| = e^{3 x + C} \\ \Rightarrow & 2 + 3 y = \pm e^{C} e^{3 x} \\ \Rightarrow & y = D e^{3 x} - \frac{2}{3} \end{matrix}$

der $D = \pm e^{C}$ er en vilkårlig konstant ulik . Vi kan også ta med $D = 0$ , siden det gir oss løsningen vi observerte i starten. Med kravet om at grafen skal gå gjennom $(0, \frac{1}{3})$ , må vi ha

$y (0) = D e^{0} - \frac{2}{3} = D - \frac{2}{3} = \frac{1}{3} .$

Dette vi . Altså må vi ha $\begin{matrix} y (x) = e^{3 x} - \frac{2}{3} . \end{matrix}$

Svar: $\begin{matrix} y (x) = e^{3 x} - \frac{2}{3} . \end{matrix}$

Mer om

Denne oppgaven er om

Differensiallikning

En likning hvor den ukjente er en funksjon og der den deriverte, funksjonens differensialkvotient, inngår.

Et eksempel er y'' - y = 0 eller $\frac{d^{2} f (x)}{d x^{2}} - f (x) = 0$

differensiallikning

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritme

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjon

For flere forklaringer og eksempler på differensiallikninger, se artikkelen Separable differensiallikninger.

Visste du at

Når du kjenner verdien til løsningsfunksjonen til en differensiallikning i ett punkt kan det ofte være vel så enkelt å benytte bestemte integraler. Etter omskrivingen $y' / (2 + 3 y) = 1$ kan vi integrere fra $0$ til en parameter $t$ med hensyn på $x$ på begge sider og få

$\begin{matrix} \int_{0}^{t} \frac{y' d x}{2 + 3 y} & = \int_{0}^{t} \frac{\frac{d y}{d x} d x}{2 + 3 y} = \int_{x = 0}^{x = t} \frac{d y}{2 + 3 y} = \int_{y = y (0)}^{y = y (t)} \frac{d y}{2 + 3 y} \\ = \int_{\frac{1}{3}}^{y (t)} \frac{d y}{2 + 3 y} = {[\frac{1}{3} \ln]}_{\frac{1}{3}}^{y (t)} = \frac{1}{3} \ln - \frac{1}{3} \ln 3 \\ = \int_{0}^{t} 1 d x = {[x]}_{0}^{t} = t . \end{matrix}$

Dette kan skrives om til $\begin{matrix} \ln (2 + 3 y (t)) = \ln 3 + 3 t \Rightarrow y (t) = e^{3 t} - \frac{2}{3}, \end{matrix}$ som er den riktige løsningen, bare som funksjon av $t$ . Symbolet $t$ ble valgt slik at vi ikke forvirret oss selv med $x$ -variabelen inne i integralet og $x$ -variabelen i grensen til integralet. Altså er det helt ufarlig å bytte ut $t$ med $x$ og ende opp med løsningen $\begin{matrix} y (x) = e^{3 x} - \frac{2}{3}, \end{matrix}$ som vi også fant ovenfor.

DEL 2 Med hjelpemidler

Oppgave 1 (6 poeng) Nettkode: E-4DGT

Punktene $A (4, 3, 1)$ , $B (2, 2, 0)$ og $C (1, 2, - 2)$ er gitt.

En setning i geometrien sier:

Et plan er entydig bestemt av tre punkter dersom disse punktene ikke ligger på en rett linje.

a)

Bruk denne setningen til å vise at punktene $A$ , $B$ og $C$ bestemmer et plan α entydig.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

For å vise at $A$ , $B$ og $C$ bestemmer et plan entydig holder det ifølge setningen å vise at de tre punktene ikke ligger på en rett linje.

Ved å finne en parametrisering av linjen $A B$ kan vi undersøke om punktet $C$ ligger på denne linjen. Hvis $C$ viser seg ikke å ligge på linjen $A B$ bestemmer $A$ , $B$ og $C$ et plan $α$ entydig. Vi observerer først at linjen $A B$ kan parametriseres ved

$\begin{matrix} \vec{O B} + t \vec{B A} & = \vec{O B} + t (\vec{O A} - \vec{O B}) = [2, 2, 0] + t ([4, 3, 1] - [2, 2, 0]) \\ = [2, 2, 0] + [2 t, t, t] = [2 + 2 t, 2 + t, t], \end{matrix}$ der $t \in ℝ$ .

Dersom $C$ ligger på linjen $A B$ må det finnes en verdi for $t$ slik at

$\begin{matrix} [2 + 2 t, 2 + t, t] = \vec{O C} = [1, 2, - 2] . \end{matrix}$

Ved å sette $x$ -verdiene like får vi $2 + 2 t = 1$ som betyr at $t = - \frac{1}{2}$ , og ved å sette $z$ -verdiene like får vi $2 + t = 2$ , som betyr at $t = 0$ . Dette er en selvmotsigelse ettersom $t$ ikke kan være både $- \frac{1}{2}$ og $0$ ! Altså finnes det ikke en verdi for $t$ som gjør at vi kan uttrykke koordinatene til $C$ ved hjelp av den parameteriserte linjen $A B$ . Med andre ord ligger ikke $A$ , $B$ og $C$ på en rett linje. Dette betyr ifølge setningen at $A$ , $B$ og $C$ bestemmer et plan $α$ entydig.

Mer om

Denne oppgaven er om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektor

Plan

Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.

plan

Punkt

I geometrien tegnes punkt som en prikk eller et kryss. Den knyttes til en fast posisjon og har ingen utstrekning. Et punkt har en stor bokstav som navn, for eksempel A eller B.

punkt

Linje

En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.

linje

For flere forklaringer og eksempler på vektorer, se artikkelen Parameterframstilling av en rett linje.

Visste du at

Dersom vi hadde forsøkt å beskrive et plan ved hjelp av tre punkter $A$ , $B$ og $C$ som ligger på en rett linje ville vi først vært interessert i å finne en normalvektor til planet. Denne finner vi vanligvis ved å kreve at den er parallell med $\vec{A B} \times \vec{A C}$ , men siden $A$ , $B$ og $C$ ligger på en rett linje må $\vec{A B}$ og $\vec{A C}$ være parallelle. Det betyr at $\vec{A B} \times \vec{A C} = 0$ . Da ville vi fått problemer med å finne likningen som beskriver planet.

b)

Bestem en likning til planet $α$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

For å finne likningen til planet $α$ må vi ha et uttrykk for en vektor som står vinkelrett på planet og minst ett punkt, eller avstanden fra planet til Origo, som ligger i planet.

Ettersom vektoren $\vec{A B} \times \vec{A C}$ står vinkelrett på både $\vec{A B}$ og $\vec{A C}$ må $\vec{A B} \times \vec{A C}$ stå vinkelrett på planet $α$ . Siden

$\begin{matrix} \vec{A B} & = \vec{O B} - \vec{O A} = [2, 2, 0] - [4, 3, 1] = [- 2, - 1, - 1] \\ \vec{A C} & = \vec{O C} - \vec{O A} = [1, 2, - 2] - [4, 3, 1] = [- 3, - 1, - 3] \end{matrix}$

finner vi at

$\vec{A B} \times \vec{A C} = |\begin{matrix} \vec{e_{x}} & \vec{e_{y}} & \vec{e_{z}} \\ - 2 & - 1 & - 1 \\ - 3 & - 1 & - 3 \end{matrix}| = |\begin{matrix} - 1 & - 1 \\ - 1 & - 3 \end{matrix}| \vec{e_{x}} - |\begin{matrix} - 2 & - 1 \\ - 3 & - 3 \end{matrix}| \vec{e_{y}} + |\begin{matrix} - 2 & - 1 \\ - 3 & - 1 \end{matrix}| \vec{e_{z}}$

$= 2 \vec{e_{x}} - 3 \vec{e_{y}} + (- 1) \vec{e_{z}} = [2, - 3, - 1] .$

Det betyr at vi kan velge normalvektoren $\vec{n} = [- 2, 3, 1]$ . Siden $A$ ligger i planet $α$ kan vi nå formulere likningen for planet ved at alle punkter $P (x, y, z)$ som ligger i $α$ må tilfredsstille

$\begin{matrix} \vec{n} \cdot \vec{A P} \Rightarrow \vec{n} \cdot (\vec{O P} - \vec{O A}) = 0 \Rightarrow \vec{n} \cdot \vec{O P} - \vec{n} \cdot \vec{O A} = 0 . \end{matrix}$

Siden

$\begin{matrix} \vec{n} \cdot \vec{O A} = [2, - 3, - 1] \cdot [4, 3, 1] = 2 \cdot 4 - 3 \cdot 3 - 1 \cdot 1 = 8 - 9 - 1 = - 2 \end{matrix}$

har vi altså at

$\begin{matrix} \vec{n} \cdot \vec{O P} + 2 = [2, - 3, - 1] \cdot [x, y, z] + 2 = 2 x - 3 y - z + 2 = 0 \end{matrix}$

er likningen for planet $α$ .

Svar: $\begin{matrix} 2 x - 3 y - z + 2 = 0 . \end{matrix}$

Mer om

Denne oppgaven er om

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektor

Plan

Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.

plan

Normalvektor

En normalvektor $\vec{n}$ for et plan står vinkelrett på alle linjer i planet.

normalvektor

Rett vinkel

En rett vinkel er 90 grader og vi skriver 90°. Vi sier da at vinkelbeina står normalt på hverandre.

rett vinkel

Punkt

I geometrien tegnes punkt som en prikk eller et kryss. Den knyttes til en fast posisjon og har ingen utstrekning. Et punkt har en stor bokstav som navn, for eksempel A eller B.

punkt

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

For flere forklaringer og eksempler på vektorer, se artikkelen Likning til et plan.

c)

Et punkt $T$ har koordinatene $(2, 5, 4 t + 1)$ .

Bestem $t$ slik at volumet av pyramiden $A B C T$ blir $3$ .

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi skal bestemme parameteren $t$ slik at volumet av pyramiden $A B C T$ blir $3$ . Dette kan vi gjøre ved først å finne volumet av pyramiden som funksjon av $t$ , for deretter å finne den verdien for $t$ som gjør at dette er lik $3$ .

Pyramiden $A B C T$ er utspent av vektorene $\vec{A B}$ , $\vec{A C}$ og $\vec{A T}$ og har derfor volum

$\begin{matrix} V = \frac{1}{6} \end{matrix} |(\vec{A B} \times \vec{A C}) \cdot \vec{A T}|$

Heldigvis har vi allerede beregnet kryssproduktet

$\vec{A B} \times \vec{A C} = [2, - 3, - 1]$ i oppgave $1 b)$ . Siden vektoren $\vec{A T}$ kan uttrykkes

$\begin{matrix} \vec{A T} = \vec{O T} - \vec{O A} = [2, 5, 4 t + 1] - [4, 3, 1] = [- 2, 2, 4 t] \end{matrix}$

kan volumet til pyramiden altså skrives

$\begin{matrix} V = \frac{1}{6} \end{matrix} |(\vec{A B} \times \vec{A C}) \cdot \vec{A T}| = \frac{1}{6} |[2, - 3, - 1] \cdot [- 2, 2, 4 t]| = \frac{1}{6} |- 4 - 6 - 4 t|$

$= \frac{1}{6} |- 2 (5 + 2 t)| = |\frac{5}{3} + \frac{2}{3} t|$

For at volumet av pyramiden skal være $3$ må altså $t$ tilfredsstille $\begin{matrix} |\frac{5}{3} + \frac{2}{3} t| = 3 . \end{matrix}$ Det er altså to verdier for $t$ som gjør at pyramidens volum er $3$ . Disse er gitt ved

$\begin{matrix} \frac{5}{3} + \frac{2}{3} t = \pm 3 \Rightarrow \frac{2}{3} t = \frac{- 5 \pm 9}{3} \Rightarrow t = \frac{3}{2} \cdot \frac{- 5 \pm 9}{3} = \frac{- 5 \pm 9}{2} . \end{matrix}$

Med andre ord er $t$ -verdiene som gjør at pyramiden $A B C T$ har volum lik $3$

$t = - 7 og t = 2$

Svar: $t = - 7 og t = 2$ .

Mer om

Denne oppgaven er om

Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm³) og kubikkmeter (m³).

volum

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektor

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

For flere forklaringer og eksempler på vektorer, se artikkelen Kryssprodukt - areal og volum.

Visste du at

At formelen for volumet av en pyramide utspent av vektorene $\vec{a}$ , $\vec{b}$ og $\vec{c}$ er $\begin{matrix} V = \frac{1}{6} \end{matrix} |(\vec{a} \times \vec{b}) \cdot \vec{c}|$ følger fra det faktum at lengden av vektoren $\vec{a} \times \vec{b}$ er lik arealet av parallellogrammet utspent av vektorene $\vec{a}$ og $\vec{b}$ . Hvis $θ$ er vinkelen mellom normalvektoren på parallellogrammet utspent av $\vec{a}$ og $\vec{b}$ og vektoren $\vec{c}$ følger det at høyden, dersom grunnflaten er $G = | \vec{a} \times \vec{b} |$ , i parallellpipedet utspent av vektorene $\vec{a}$ , $\vec{b}$ og $\vec{c}$ er gitt som $h = |\vec{c}| |\cos (θ)|$ . Siden

$|(\vec{a} \times \vec{b}) \cdot \vec{c}| \begin{matrix} = |\vec{a} \times \vec{b}| \cdot |\vec{c}| |\cos (θ)| = G \cdot h \end{matrix}$

er $| (\vec{a} \times \vec{b}) \cdot \vec{c} |$ volumet av parallellpipedet utspent av vektorene $\vec{a}$ , $\vec{b}$ og $\vec{c}$ . Etter litt tenking og tegning kan man overbevise seg om at pyramiden utspent av $\vec{a}$ , $\vec{b}$ og $\vec{c}$ utgjør nøyaktig $\frac{1}{6}$ av parallellepipedet utspent av de samme vektorene.

Oppgave 2 (5 poeng) Nettkode: E-4DGY

En kuleflate er gitt ved likningen

$x^{2} + y^{2} + z^{2} - 2 x - 2 y - 6 z + 2 = 0$

a)

Vis at punktet $P (2, 3, 5)$ ligger på kuleflaten.

Løs oppgaven her

Løsningsforslag a)

Tanker

Punktet $P$ ligger på kuleflaten hvis, og bare hvis, koordinatene til $P$ tilfredsstiller likningen for kuleflaten.

Ved å sette inn koordinatene til $P$ i likningen for kuleflaten finner vi $\begin{matrix} 2^{2} + 3^{2} + 5^{2} - 2 \cdot 2 - 2 \cdot 3 - 6 \cdot 5 + 2 = 0, \end{matrix}$ og siden $\begin{matrix} 2^{2} + 3^{2} + 5^{2} - 2 \cdot 2 - 2 \cdot 3 - 6 \cdot 5 + 2 & = 4 + 9 + 25 - 4 - 6 - 30 + 2 \\ = 38 - 40 + 2 = 0 \end{matrix}$ er punktet $P$ blant de punktene som tilfredsstiller likningen for kuleflaten. Med andre ord ligger $P$ på kuleflaten.

Mer om

Denne oppgaven er om

Kule

Et tredimensjonalt objekt der alle punktene på overflaten har en fast avstand til sentrum i objektet. Denne avstanden fra et punkt på overflaten til sentrum kalles radius.

kule

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

Punkt

I geometrien tegnes punkt som en prikk eller et kryss. Den knyttes til en fast posisjon og har ingen utstrekning. Et punkt har en stor bokstav som navn, for eksempel A eller B.

punkt

For flere forklaringer og eksempler på kuler, se artikkelen Likning for en kule.

b)

Bestem sentrum og radius til kulen.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Ved å manipulere likningen for kuleflaten slik at den blir på formen $(x - x_{0})^{2} + (y - y_{0})^{2} + (z - z_{0})^{2} = R^{2}$ kan vi lese av sentrum og radius til kulen.

Ved å benytte omskrivingen

$\begin{matrix} x^{2} + y^{2} + z^{2} - 2 x - 2 y - 6 z + 2 \\ = & x^{2} - 2 \cdot x + y^{2} - 2 \cdot y + z^{2} - 2 \cdot 3 z + 2 \\ = & (x - 1)^{2} - 1 + (y - 1)^{2} - 1 + (z - 3)^{2} - 9 + 2 \\ = & (x - 1)^{2} + (y - 1)^{2} + (z - 3)^{2} - 3^{2} \end{matrix}$

kan likningen for kuleflaten omformuleres til $\begin{matrix} (x - 1)^{2} + (y - 1)^{2} + (z - 3)^{2} = 3^{2} . \end{matrix}$ Fra Pythagoras læresetning kan vi konkludere med at de punktene $(x, y, z)$ som tilfredsstiller likningen for kuleflaten er nøyaktig de punktene som har avstand $3$ fra punktet $(1, 1, 3)$ . Dette betyr at kulen har sentrum i $S (1, 1, 3)$ og radius $3$ .

Svar: Kulen har sentrum i $S (1, 1, 3)$ og radius $3$ .

Mer om

Denne oppgaven er om

Kule

Et tredimensjonalt objekt der alle punktene på overflaten har en fast avstand til sentrum i objektet. Denne avstanden fra et punkt på overflaten til sentrum kalles radius.

kule

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

Pytagoras læresetning

Pytagoras læresetning sier at:

Arealet av kvadratet utspent av hypotenusen i en rettvinklet trekant er lik summen av arealene til kvadratene utspent av katetene.

Hvis lengden av katetene er a og b, og lengden av hypotenusen er c, har vi denne sammenhengen : $a^{2} + b^{2} = c^{2}$

Setningen kan brukes til å finne lengden til en side i en trekant.

Pythagoras læresetning

For flere forklaringer og eksempler på kuler, se artikkelen Likning for en kule.

c)

Bestem likningen til planet som tangerer kuleflaten i punktet $P$ .

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Likningen til planet som tangerer kuleflaten i $P$ kan uttrykkes dersom vi finner en vektor som står normalt på planet, og et punkt som ligger i planet.

Siden enhver linje fra sentrum i kulen til kuleflaten står vinkelrett på kuleflaten kan vi velge vektoren $\vec{S P}$ fra sentrum $S$ i kulen til punktet $P$ som normalvektor til tangentplanet i $P$ . Siden $P$ ligger i planet må alle punkter $Q (x, y, z)$ som ligger i planet tilfredsstille

$\begin{matrix} \vec{S P} \cdot \vec{P Q} = 0 . \end{matrix}$

Siden

$\begin{matrix} \vec{S P} & = \vec{O P} - \vec{O S} = [2, 3, 5] - [1, 1, 3] = [1, 2, 2] \end{matrix}$

$\begin{matrix} \vec{P Q} = \vec{O Q} - \vec{O P} = [x, y, z] - [2, 3, 5] = [x - 2, y - 3, z - 5] \end{matrix}$

må altså

$\begin{matrix} \vec{S P} \cdot \vec{P Q} & = [1, 2, 2] \cdot [x - 2, y - 3, z - 5] = x - 2 + 2 (y - 3) + 2 (z - 5) \\ = x + 2 y + 2 z - 2 - 6 - 10 = x + 2 y + 2 z - 18 = 0 . \end{matrix}$

Med andre ord er likningen til planet som tangerer kuleflaten i $P$ $\begin{matrix} x + 2 y + 2 z - 18 = 0 . \end{matrix}$

Svar: $\begin{matrix} x + 2 y + 2 z - 18 = 0 \end{matrix}$

Mer om

Denne oppgaven er om

Kule

Et tredimensjonalt objekt der alle punktene på overflaten har en fast avstand til sentrum i objektet. Denne avstanden fra et punkt på overflaten til sentrum kalles radius.

kule

Vektor

En vektor er en størrelse med en retning.

I planet er en vektor et linjestykke med retning. Vi beskriver en vektor fra origo med koordinatene for endepunktet til vektoren.

Eksempel: Figuren viser en vektor fra origo til punktet (2,3). Vi kan skrive at vektor v = $[2, 3]$ .

vektor

Normalvektor

En normalvektor $\vec{n}$ for et plan står vinkelrett på alle linjer i planet.

normalvektor

Rett vinkel

En rett vinkel er 90 grader og vi skriver 90°. Vi sier da at vinkelbeina står normalt på hverandre.

rett vinkel

Tangent

Tangent er en linje som berører en kurve i et punkt. Vi sier at linjen tangerer kurven i det punktet.

tangent

Plan

Et plan har uendelig utstrekning i to dimensjoner. Vi kan tenke på ei slett, uendelig tynn papirflate.

plan

For flere forklaringer og eksempler på vektorer, se artikkelen Likning til et plan.

Oppgave 3 (7 poeng) Nettkode: E-4DH7

I en kriminalserie på TV ble et drapsoffer funnet kl. 11.00. Kroppstemperaturen ble da målt til 30°C . Rommet der den drepte ble funnet, hadde hatt en konstant temperatur på 22°C siden mordet skjedde.

Vi lar kroppstemperaturen være $y (t)$ grader Celsius $t$ timer etter at den døde ble funnet.

a)

Ifølge Newtons avkjølingslov er temperaturendringen per time proporsjonal med differansen mellom kroppstemperaturen og romtemperaturen. Forklar at dette gir differensiallikningen

$y' = - k (y - 22)$ der $k > 0$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Siden Newtons avkjølingslov nevner både temperatur og dens endring over tid vil den kunne skrives som en første ordens differensiallikning.

Newtons avkjølingslov sier at temperaturendringen per time, $y' (t)$ , er proporsjonal med differansen mellom kroppstemperaturen $y (t)$ og romtemperaturen $22^{\circ} C$ . Med andre ord er den tidsderiverte av kroppstemperaturen, $y' (t)$ , proporsjonal med $(y (t) - 22)$ . At to størrelser $A$ og $B$ er proporsjonale betyr at det finnes en konstant $γ$ slik at $A = γ B$ . Vi kan altså konstatere Newtons avkjølingslov ved $\begin{matrix} y' (t) = γ (y (t) - 22) . \end{matrix}$ Vi kan faktisk si litt mer om situasjonen. Vi vet nemlig at kroppstemperaturen, som begynte lik $30^{\circ} C$ , vil nærme seg rommets temperatur. Med andre ord må $y' (t)$ være negativ. Siden $y (t) - 22$ alltid er positiv må $γ$ alltid være negativ. Det betyr at vi kan skrive $γ = - k$ , for en positiv konstant $k$ . Vi kan oppsummere situasjonen i differensiallikningen

$y' = - k (y - 22) for k > 0$

Mer om

Denne oppgaven er om

Differensiallikning

En likning hvor den ukjente er en funksjon og der den deriverte, funksjonens differensialkvotient, inngår.

Et eksempel er y'' - y = 0 eller $\frac{d^{2} f (x)}{d x^{2}} - f (x) = 0$

differensiallikning

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

For flere forklaringer og eksempler på derivasjon, se artikkelen Proporsjonalitet.

b)

Forklar at $y (0) = 30$ , og løs differensiallikningen ved regning.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

At $y (0) = 30$ gir oss et krav til løsningene av differensiallikningen

$L : y' = - k (y - 22) for k > 0$ .

Vi kan da bestemme den løsningen som passer med vår situasjon.

Ifølge definisjonen av $y (t)$ , skal $y (0)$ være kroppstemperaturen målt i grader celsius $0$ timer etter at den døde ble funnet. Det tilsvarer funntidspunktet, og da var temperaturen $30$ grader celsius. Dermed må $y (0) = 30$ .

Vi skal løse differensiallikningen

$y^{'} = - k (y - 22)$ .

Først omformer vi den slik at vi kan finne den integrerende faktoren.

$y^{'} + k y = 22 k$ .

Den integrerende faktoren blir $e^{k t}$ , så vi multipliserer med den på begge sider. Det gir

$y^{'} e^{k t} + k e^{k t} y = 22 k e^{k t} .$

Venstre side er den deriverte til produktet $y e^{k t}$ . Derfor er

${(y e^{k t})}^{'} = 22 k e^{k t}$

Nå integrerer vi begge sider med hensyn på $t$ og kombinerer de to integrasjonskonstantene til én konstant på høyre side.

$\begin{matrix} y e^{k t} & = & 22 e^{k t} + C \\ y & = & 22 + C e^{- k t} \end{matrix}$

Vi vet at $y (0) = 30$ så

$y (0) = 22 + C e^{0} = 22 + C = 30$

Dette gir $C = 8$ . Dermed er løsningen på initialverdiproblemet

$y (t) = 8 e^{- k t} + 22$

Svar: $\begin{matrix} y (t) = 8 e^{- k t} + 22 \end{matrix}$

Mer om

Denne oppgaven er om

Differensiallikning

En likning hvor den ukjente er en funksjon og der den deriverte, funksjonens differensialkvotient, inngår.

Et eksempel er y'' - y = 0 eller $\frac{d^{2} f (x)}{d x^{2}} - f (x) = 0$

differensiallikning

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

For flere forklaringer og eksempler på differensiallikninger, se artikkelen Separable differensiallikninger.

Visste du at

Vi kan fort undersøke om løsningen av en differensiallikning er den riktige. Ved å derivere $y (t) = 8 e^{- k t} + 22$ finner vi $\begin{matrix} y' (t) = - 8 k e^{- k t}, \end{matrix}$ og ifølge differensiallikningen skal $\begin{matrix} - 8 k e^{- k t} = y' = - k (y - 22) = - k (8 e^{- k t} + 22 - 22) = - 8 k e^{- k t} . \end{matrix}$ Siden denne stemmer vet vi at $y (t) = 8 e^{- k t} + 22$ er en løsning av differensiallikningen, og siden $\begin{matrix} y (0) = 8 e^{0} + 22 = 8 + 22 = 30, \end{matrix}$ overholder den spesielle løsningen kravet om at $y (0) = 30$ .

c)

En time etter at den døde ble funnet, ble kroppstemperaturen målt til 28 °C . Bruk dette til å bestemme konstanten $k$ .

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

At kroppstemperaturen til den døde var $28^{\circ} C$ ved tiden $t = 1$ kan vi skrive som et krav på $y (t)$ . Sammen med løsningen av differensiallikningen fra oppgave $3 b)$ kan dette kravet brukes til å bestemme $k$ .

Siden kroppstemperaturen til den døde var $28^{\circ} C$ ved tiden $t = 1$ må $y (1) = 28$ . Denne oppførselen kan vi kreve av funksjonen fra oppgave $3 b)$ ved $\begin{matrix} 28 = y (1) = 8 e^{- k} + 22 . \end{matrix}$ Dette kan omformuleres ved $\begin{matrix} 28 = 8 e^{- k} + 22 \Rightarrow \frac{3}{4} = e^{- k} \\ \Rightarrow & - k = \ln \frac{3}{4} \Rightarrow k = - \ln \frac{3}{4} = \ln \frac{4}{3} \approx 0, 288 . \end{matrix}$ Dette betyr at $k$ er omtrent lik $0, 288$ per time.

Svar: $k \approx 0, 288 per time$

Mer om

Denne oppgaven er om

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjon

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritme

For flere forklaringer og eksempler på likninger, se artikkelen Eksponentiallikninger.

d)

Vi antar at drapsofferet hadde en kroppstemperatur på 37°C like etter at døden inntraff.

Bruk $y (t)$ til å anslå når drapet ble utført.

Løs oppgaven her

Løsningsforslag d)

Jeg tenker

Vi ønsker å finne tidspunktet, $t$ , som svarer til det tidspunktet der drapsofferet hadde en kroppstemperatur på $37^{\circ} C$ .

Siden drapsofferet hadde en kroppstemperatur på $37^{\circ} C$ like etter at døden inntraff må tidpunktet, $t$ , døden inntraff tilfredsstille likningen $y (t) = 37$ . Det betyr at $\begin{matrix} y (t) = 8 e^{- k t} + 22 = 37 \Rightarrow e^{- k t} = \frac{15}{8} \\ \Rightarrow & - k t = \ln \frac{15}{8} \Rightarrow t = - \frac{1}{k} \ln \frac{15}{8}, \end{matrix}$ og siden $k \approx 0, 288$ følger det at $\begin{matrix} t \approx - \frac{1}{0, 288} \ln \frac{15}{8} \approx - 2, 183 . \end{matrix}$ Det betyr at døden inntraff $2, 183$ timer før offeret ble funnet. Offeret ble funnet klokken 11:00, og siden $0, 183$ timer tilsvarer $0, 183 \cdot 60 = 10, 98$ minutter, må drapet ha blitt utført klokken $08 : 49$ .

Svar: Drapet ble utført klokken $08 : 49$ .

Mer om

Denne oppgaven er om

Eksponentialfunksjon

En matematisk funksjon på formen a^x. Funksjonen er et potensuttrykk der x er eksponenten.

Brukes mest om funksjonen e^x.

eksponentialfunksjon

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritme

For flere forklaringer og eksempler på likninger, se artikkelen Logaritmelikninger.

Oppgave 4 (7 poeng) Nettkode: E-4DHC

En uendelig rekke er gitt ved

$1 + x + x^{2} + x^{3} + . . .$

a)

Vis at $1 + x + x^{2} + x^{3} + . . . = \frac{1}{1 - x}$ , når $x \in ⟨- 1, 1⟩$

Det kan vises at

$(1)' + (x)' + (x^{2})' + (x^{3})' + . . . = (\frac{1}{1 - x})'$ , når $x \in ⟨- 1, 1⟩$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Vi må vise at en uendelig sum av ledd på formen $x^{n}$ , der $n$ er et heltall, konvergerer mot et tall dersom $x \in (- 1, 1)$ og at dette tallet kan skrives $1 / (1 - x)$ .

Siden en endelig geometrisk rekke $\begin{matrix} G_{n} = 1 + x + x^{2} + x^{3} + . . . + x^{n} \end{matrix}$ tilfredsstiller

$\begin{matrix} x G_{n} = & x + x^{2} + x^{3} + x^{4} + . . . + x^{n} + x^{n + 1} \\ = & 1 + x + x^{2} + x^{3} + x^{4} + . . . + x^{n} + x^{n + 1} - 1 \\ = & G_{n} + x^{n + 1} - 1 \end{matrix}$

kan vi skrive $\begin{matrix} x G_{n} - G_{n} = x^{n + 1} - 1, \end{matrix}$ eller helt tilsvarende $\begin{matrix} G_{n} (1 - x) = 1 - x^{n + 1} . \end{matrix}$ Verdien av en endelig geometrisk rekke er altså $\begin{matrix} G_{n} = 1 + x + x^{2} + x^{3} + . . . + x^{n} = \frac{1 - x^{n + 1}}{1 - x} . \end{matrix}$ En uendelig geometrisk rekke oppstår når $n$ går mot uendelig. Hvis $x \in (- 1, 1)$ må da $x^{n + 1}$ gå mot $0$ og dermed også $\begin{matrix} 1 + x + x^{2} + x^{3} + . . . = \frac{1}{1 - x} . \end{matrix}$

Mer om

Denne oppgaven er om

Uendelige rekker

En rekke er en sum av elementene i en tallfølge. Rekken kalles uendelig hvis den består av uendelig antall elementer.

Eksempel : $\sum_{n = 1}^{\infty} x_{n}$

( ∞ er tegnet for uendelighet )

uendelig rekke

Sum

Resultatet av en addisjon.

Eksempel: 2 + 5 + 1 = 8, her kalles 8 for sum.

sum

Konvergens

Konvergens betyr i matematikk å nærme seg en grense.

Se Konvergent tallfølge

konvergens

Heltall

Heltall er de tallene vi oftest teller: 0, 1, 2, 3, 4... De hele tallene inkluderer også de negative tallene; -1, -2, -3...

Symbolet for mengden av hele tall er ℤ.

heltall

Polynom

Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.

Eksempler: $4 x + 5$ og $12 x + 2 a$ .

polynom

For flere forklaringer og eksempler på rekker, se artikkelen Geometriske rekker.

Visste du at

Det tok matematikere nesten $100$ år å finne verdien av en rekke som ved første øyekast likner på en geometrisk rekke. Rekken, som har fått navnet ”Baselproblemet”, er som følger: $\begin{matrix} \frac{1}{1^{2}} + \frac{1}{2^{2}} + \frac{1}{3^{2}} + . . . + \frac{1}{n^{2}} + . . . \end{matrix}$ I $1734$ fant den store matematikeren Leonhard Euler at løsningen var $π^{2} / 6$ . Hva $π$ , som er forholdet mellom omkrets og diameter i en sirkel, har med denne rekken å gjøre er ikke lett å se ved første øyekast.

b)

Vis at

$1 + 2 x + 3 x^{2} + 4 x^{3} + . . . = \frac{1}{{(1 - x)}^{2}}$ , når $x \in ⟨- 1, 1⟩$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Siden det kan vises at summen av den deriverte til hvert ledd i en uendelig geometrisk rekke er lik den deriverte av det tallet rekken konvergerer mot kan vi sette opp en likning. Forhåpentligvis er det denne likningen vi ønsker å finne.

Siden

$(1)' + (x)' + (x^{2})' + (x^{3})' + . . . = (\frac{1}{1 - x})' når x \in (- 1, 1)$

og $(x^{n})' = n x^{n - 1}$ for alle heltall $n$ , kan vi skrive

$0 + 1 + 2 x + 3 x^{2} + 4 x^{3} + . . . = (\frac{1}{1 - x})' når x \in (- 1, 1),$

Fra kjerneregelen med kjerne $g (x) = (1 - x)$ følger det videre at

$\begin{matrix} {(\frac{1}{1 - x})}^{'} = & {(\frac{1}{g (x)})}^{'} \\ = & - \frac{1}{{(g (x))}^{2}} \cdot g^{'} (x) \\ = & - \frac{1}{{(1 - x)}^{2}} \cdot (- 1) \\ = & \frac{1}{{(1 - x)}^{2}} \end{matrix}$

Vi sitter altså igjen med følgende likhet

$1 + 2 x + 3 x^{2} + 4 x^{3} + . . . = \frac{1}{{(1 - x)}^{2}} når x \in (- 1, 1),$

som er det vi ønsket å vise.

Mer om

Denne oppgaven er om

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

Polynom

Et reelt polynom er en sum av produkter av en eller flere ukjente og reelle tall.

Eksempler: $4 x + 5$ og $12 x + 2 a$ .

polynom

Uendelige rekker

En rekke er en sum av elementene i en tallfølge. Rekken kalles uendelig hvis den består av uendelig antall elementer.

Eksempel : $\sum_{n = 1}^{\infty} x_{n}$

( ∞ er tegnet for uendelighet )

uendelig rekke

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

For flere forklaringer og eksempler på derivasjon, se artikkelen Derivasjonsregler.

c)

Bruk resultatet i oppgave b) til å vise at

$1 + \frac{2}{2^{1}} + \frac{3}{2^{2}} + \frac{4}{2^{3}} + . . . = 4$

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Ved å bruke en passende $x \in (- 1, 1)$ i resultatet fra oppgave $b)$ kan vi finne en ny måte å skrive tallet $4$ .

Siden $\frac{1}{2} \in (- 1, 1)$ og $\begin{matrix} 4 = \frac{1}{(\frac{1}{4})} = \frac{1}{{(\frac{1}{2})}^{2}} = \frac{1}{{(1 - \frac{1}{2})}^{2}}, \end{matrix}$ følger det fra resultatet i oppgave $b)$ at $\begin{matrix} 1 + 2 (\frac{1}{2}) + 3 {(\frac{1}{2})}^{2} + 4 {(\frac{1}{2})}^{3} + . . . = 4 . \end{matrix}$ Dette kan omskrives til $\begin{matrix} 1 + \frac{2}{2^{1}} + \frac{3}{2^{2}} + \frac{4}{2^{3}} + . . . = 4, \end{matrix}$ som er det vi ønsket å vise.

Mer om

Denne oppgaven er om

Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.

Brøk kan sees som et tall på tallinja eller som del av en mengde.

brøk

Sum

Resultatet av en addisjon.

Eksempel: 2 + 5 + 1 = 8, her kalles 8 for sum.

sum

For flere forklaringer og eksempler på rekker, se artikkelen Uendelige rekker.

d)

Bruk induksjon til å bevise påstanden

$P (n) : 1 + \frac{2}{2^{1}} + \frac{3}{2^{2}} + \frac{4}{2^{3}} + . . . + \frac{n}{2^{n - 1}} = 4 - \frac{n + 2}{2^{n - 1}}, n \in ℕ$

Løs oppgaven her

Løsningsforslag d)

Jeg tenker

Vi må både vise at $P (1)$ og at hvis påstanden stemmer for $n = k$ så må den også stemme for $n = k + 1$ .

For $n = 1$ sier påstanden at $\begin{matrix} P (1) : 1 = 4 - \frac{1 + 2}{2^{1 - 1}} \Leftrightarrow 1 = 4 - 3, \end{matrix}$ som er sant. Altså gjenstår det bare å undersøke om $P (k + 1)$ nødvendigvis må være sann hvis $P (k)$ er sann. Vi antar altså at $\begin{matrix} P (k) : 1 + \frac{2}{2^{1}} + \frac{3}{2^{2}} + \frac{4}{2^{3}} + . . . + \frac{k}{2^{k - 1}} = 4 - \frac{k + 2}{2^{k - 1}} \end{matrix}$ og bruker dette til å undersøke om $\begin{matrix} P (k + 1) : 1 + \frac{2}{2^{1}} + \frac{3}{2^{2}} + \frac{4}{2^{3}} + . . . + \frac{k + 1}{2^{k}} = 4 - \frac{k + 3}{2^{k}} . \end{matrix}$ Ved å legge til $\frac{k + 1}{2^{k}}$ på begge sider av likhetstegnet i $P (k)$ følger det at $\begin{matrix} 1 + \frac{2}{2^{1}} + \frac{3}{2^{2}} + \frac{4}{2^{3}} + . . . + \frac{k}{2^{k - 1}} + \frac{k + 1}{2^{k}} = 4 - \frac{k + 2}{2^{k - 1}} + \frac{k + 1}{2^{k}} \end{matrix}$ og siden

$\begin{matrix} - \frac{k + 2}{2^{k - 1}} + \frac{k + 1}{2^{k}} & = & - \frac{2 k + 4}{2^{k}} + \frac{k + 1}{2^{k}} \\ = & \frac{- 2 k - 4 + k + 1}{2^{k}} \\ = & \frac{- k - 3}{2^{k}} = - \frac{k + 3}{2^{k}} \end{matrix}$

kan vi skrive $\begin{matrix} 1 + \frac{2}{2^{1}} + \frac{3}{2^{2}} + \frac{4}{2^{3}} + . . . + \frac{k}{2^{k - 1}} + \frac{k + 1}{2^{k}} = 4 - \frac{k + 3}{2^{k}} . \end{matrix}$ Dette er nøyaktig påstanden $P (k + 1)!$ Det betyr at $P (k + 1)$ følger direkte fra $P (k)$ og siden vi i tillegg vet at $P (1)$ så må $P (n)$ for alle $n \in ℕ$ ved induksjon.

Mer om

Denne oppgaven er om

Matematisk induksjon

En metode til å bevise en påstand P(n) der det inngår et positivt heltall n. Følgende to skritt må gjennomføres:

Bevis påstanden for n =1.
Bevis at for ethvert positivt tall k vil man fra hypotesen P(k) kunne slutte at hypotesen også gjelder for P(k+1).

Siden vi vet fra 1. at hypotesen gjelder for P(1) kan vi ved hjelp av 2. slutte at den også gjelder for P(2). Fra dette kan vi slutte at den også må gjelde for P(3), og så videre for alle P(n).

matematisk induksjon

Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.

Brøk kan sees som et tall på tallinja eller som del av en mengde.

brøk

Sum

Resultatet av en addisjon.

Eksempel: 2 + 5 + 1 = 8, her kalles 8 for sum.

sum

For flere forklaringer og eksempler på bevisføring, se artikkelen Induksjonsbevis.

Visste du at

Dersom vi ikke kjente til induksjonsbevis kunne vi brukt en ganske utradisjonell metode for å vise $P (n)$ . Ved å sette $x = \frac{1}{2}$ kan vi skrive $\begin{matrix} 1 + \frac{2}{2^{1}} + \frac{3}{2^{2}} + \frac{4}{2^{3}} + . . . + \frac{n}{2^{n - 1}} = 1 \cdot x^{0} + 2 \cdot x^{1} + 3 \cdot x^{2} + . . . + n \cdot x^{n - 1}, \end{matrix}$ og siden $(x^{n})' = n x^{n - 1}$ kan vi skrive

$\begin{matrix} 1 \cdot x^{0} + 2 x^{1} + 3 x^{2} + . . . + n x^{n - 1} = {(x + x^{2} + x^{3} + . . . + x^{n})}^{'} . \end{matrix}$

Dette er den deriverte av en endelig geometrisk rekke med verdi $\frac{x - x^{n + 1}}{1 - x}$ , som betyr at

${(x + x^{2} + x^{3} + . . . + x^{n})}^{'} \begin{matrix} = {(\frac{x - x^{n - 1}}{1 - x})}^{'} = \frac{n x^{n + 1} - (n + 1) x^{n} + 1}{(1 - x)^{2}} . \end{matrix}$

Vi kan nå sette inn for $x = \frac{1}{2}$ og dermed finne at

$\begin{matrix} \frac{n x^{n + 1} - (n + 1) x^{n} + 1}{(1 - x)^{2}} & = & \frac{\frac{n}{2^{n + 1}} - (n + 1) \frac{1}{2^{n}} + 1}{(1 - \frac{1}{2})^{2}} \\ = & \frac{- \frac{1}{2} \frac{n}{2^{n}} - \frac{1}{2^{n}} + 1}{\frac{1}{2^{2}}} \\ = & \frac{- n - 2 + 2^{n + 1}}{2^{n - 1}} \\ = & 4 - \frac{n + 2}{2^{n - 1}}, \end{matrix}$

som er nøyaktig det påstanden $P (n)$ hevder.

e)

Bruk det du har funnet ovenfor til å bestemme $\lim_{n \to \infty} \frac{n + 2}{2^{n - 1}}$

Løs oppgaven her

Løsningsforslag e)

Jeg tenker

Vi kjenner både verdien av den endelige rekken i d) og rekkens grenseverdi når $n$ går mot uendelig. Ved å kombinere disse kan vi uttrykke $\lim_{n \to \infty} \frac{n + 2}{2^{n - 1}}$ .

Siden

$1 + \frac{2}{2^{1}} + \frac{3}{2^{2}} + \frac{4}{2^{3}} + . . . + \frac{n}{2^{n - 1}} = 4 - \frac{n + 2}{2^{n - 1}} for alle n \in ℕ$

$\lim_{n \to \infty} (1 + \frac{2}{2^{1}} + \frac{3}{2^{2}} + \frac{4}{2^{3}} + . . . + \frac{n}{2^{n - 1}}) = 1 + \frac{2}{2^{1}} + \frac{3}{2^{2}} + \frac{4}{2^{3}} + . . . = 4$

må $\begin{matrix} \lim_{n \to \infty} (4 - \frac{n + 2}{2^{n - 1}}) = 4 . \end{matrix}$

Ved å bruke at grenseverdien av en sum er lik summen av grenseverdiene kan vi skrive $\begin{matrix} 4 - \lim_{n \to \infty} \frac{n + 2}{2^{n - 1}} = 4, \end{matrix}$ som betyr at $\begin{matrix} \lim_{n \to \infty} \frac{n + 2}{2^{n - 1}} = 0 . \end{matrix}$

Svar: $\begin{matrix} \lim_{n \to \infty} \frac{n + 2}{2^{n - 1}} = 0 \end{matrix}$

Mer om

Denne oppgaven er om

Grenseverdi

En uendelig tallfølge a₁, a₂, a₃, ...har grenseverdi A dersom vi kan få a_n så nær A vi vil ved å velge n stor nok.

grenseverdi

Sum

Resultatet av en addisjon.

Eksempel: 2 + 5 + 1 = 8, her kalles 8 for sum.

sum

Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.

Brøk kan sees som et tall på tallinja eller som del av en mengde.

brøk

For flere forklaringer og eksempler på grenseverdier, se artikkelen Grenseverdisetningene.

Oppgave 5 (5 poeng) Nettkode: E-4DHJ

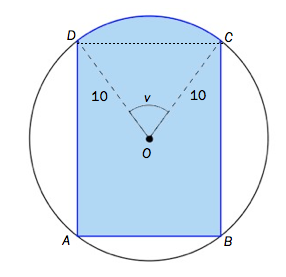
Et rektangel $A B C D$ er innskrevet i en sirkel. Sirkelen har sentrum i $O$ og radius $10$ .

Vi setter $∠ C O D = v$ , der $0 < v < π$ . Se figuren nedenfor.

a)

Vis ved regning at arealet $F$ av sirkelsektoren $C O D$ er

$F (v) = 50 v$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Arealet av sirkelsektoren $C O D$ i forhold til hele sirkelen er ganske lik vinkelen $v$ i forhold til $2 π$ .

Forholdet mellom arealet $F (v)$ av sirkelsektoren $C O D$ og hele sirkelen er lik forholdet mellom vinkelen $v$ og $2 π$ . Arealet av sirkelen er $π R^{2}$ , der $R$ er radius i sirkelen, og gir at $\begin{matrix} \frac{F (v)}{π R^{2}} = \frac{v}{2 π} . \end{matrix}$ Det betyr at $\begin{matrix} F (v) = \frac{v π R^{2}}{2 π} = \frac{v R^{2}}{2}, \end{matrix}$ og siden radius i sirkelen er $10$ , følger det at $\begin{matrix} F (v) = \frac{10^{2} v}{2} = \frac{100 v}{2} = 50 v . \end{matrix}$

Svar: $\begin{matrix} F (v) = 50 v \end{matrix}$

Mer om

Denne oppgaven er om

Sirkelsektor

Se Sektor

sirkelsektor

Sirkel

Sirkel brukes i to betydninger:

1) Selve sirkellinjen som er den krumme linjen som går gjennom punktene som har samme avstand fra et fast punkt, nemlig sentrum i sirkelen. Dette er det samme som sirkelen sin omkrets.

2) Flaten som sirkellinjen begrenser.

Areal: $A = π r^{2}$
Omkrets: $O = 2 π r$

sirkel

Pi (π)

$π$ er forholdet mellom sirkelens omkrets og diameter. Dette forholdet er alltid konstant og tilnærmet lik 3,14.

For flere forklaringer og eksempler på sirkler, se artikkelen Alt om sirkel.

b)

Vis ved regning at arealet $T$ av det fargelagte området på figuren kan skrives som

$T (v) = 50 (v + 3 \sin v)$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi kan uttrykke det fargelagte arealet $T$ ved først å dele det opp i figurer det er lettere å finne arealet til.

Vi deler opp arealet $T$ i trekantene $△ A D O$ , $△ A C B$ og sirkelsektoren $C O D$ .

Siden $A D C B$ er et rektangel må $A B = D C$ og $D A = C B$ . Videre er

$R \cdot \cos (\frac{v}{2}) = \frac{D A}{2} og R \cdot \sin (\frac{v}{2}) = \frac{D C}{2},$

som betyr at

$D A = 2 R \cos (\frac{v}{2}) og D C = 2 R \sin (\frac{v}{2}) .$

Hvis vi velger $D A$ som grunnlinje for $△ A D O$ er høyden lik $\frac{D C}{2}$ . Derfor må arealet av $△ A D O$ være

$\begin{matrix} A_{Δ A D O} & = & \frac{1}{2} D A \frac{D C}{2} \\ = & R^{2} \cos (\frac{v}{2}) \sin (\frac{v}{2}) \\ = & 10^{2} \cdot \frac{1}{2} \sin (v) \\ = & 50 \sin (v) \end{matrix}$

Siden $△ A C B$ har høyde $B C$ hvis den har grunnlinje $A B$ følger det at arealet av $△ A C B$ er

$\begin{matrix} A_{Δ A C B} & = & \frac{1}{2} B C \cdot A B \\ = & {2 R}^{2} \cos (\frac{v}{2}) \sin (\frac{v}{2}) \\ = & 2 \cdot 100 \cdot \frac{1}{2} \sin (v) \\ = & 100 \sin (v) \end{matrix}$

Siden vi har fra oppgave $a)$ at arealet av sirkelsektoren $C O D$ er $F (v) = 50 v$ må $\begin{matrix} T (v) & = & A_{△ A D O} + A_{△ A C B} + F (v) \\ = & 50 \sin (v) + 100 \sin (v) + 50 v \\ = & 50 (v + 3 \sin (v)) . \end{matrix}$

Alternativ løsning

Arealsetningen gir

$A_{Δ A O D} = \frac{1}{2} R^{2} \sin (π - v) = \frac{1}{2} R^{2} \sin (v) = A_{Δ D O C}$

Videre er

$A_{Δ A B C} = A_{Δ A C D} = A_{Δ A O D} + A_{Δ D O C} = 2 A_{Δ D O C}$

Arealet av figuren blir da

$A_{Δ A O B} + A_{Δ A B C} + A_{s e k t o r} = 3 \cdot A_{Δ D O C} + A_{s e k t o r}$

$= 3 \cdot \frac{1}{2} \cdot 10^{2} \sin (v) + 50 v = 50 (v + 3 \sin (v))$

Dette viser at

$\begin{matrix} T (v) = 50 (v + 3 \sin v) . \end{matrix}$

Svar: $\begin{matrix} T (v) = 50 (v + 3 \sin v) . \end{matrix}$

Mer om

Denne oppgaven er om

Sinus

sinus

Cosinus

Cosinus er en trigonometrisk funksjon.
Cosinus til en spiss vinkel i en rettvinklet trekant er lik forholdet mellom lengden til hosliggende katet og hypotenus.

cosinus

Sirkelsektor

Se Sektor

sirkelsektor

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

Linje

En rett linje som vanligvis kalles linje, er en rett strek som har en posisjon og retning. En linje fortsetter uendelig i begge retninger.

linje

For flere forklaringer og eksempler på trigonometriske funksjoner, se artikkelen Sinus, cosinus og tangens.

c)

Bestem $v$ grafisk slik at $T$ blir størst mulig. Bestem $T_{maks}$ .

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Vi kan benytte GeoGebras grafdel til å numerisk beregne koordinatene til toppunktet.

Ved å definere arealet $T (v)$ som en funksjon av $v$ i GeoGebras grafdel med kommandoen
T(v):=Dersom[0<v<\pi,50*(v+3sin(v))]

kan vi finne toppunktet, som er funksjonens eneste ekstremalpunkt i intervallet $[0, 4]$ , ved å bruke kommandoen
Ekstremalpunkt[T,0,4]

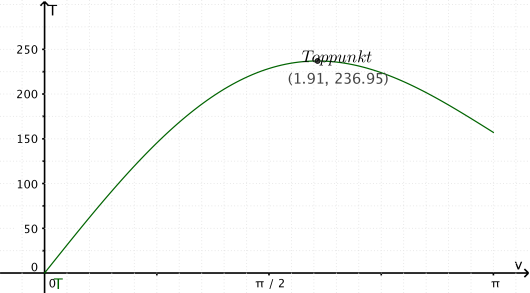
Resultatet er punktet $\begin{matrix} (1.91, 236.95) . \end{matrix}$ Altså er $v \approx 1, 91$ den vinkelen som gjør at $T$ blir størst mulig. Den makismale verdien av $T$ , $T_{m a k s}$ , er da $236, 95$ .

Svar: $v \approx 1, 91 og T_{m a k s} \approx 236, 95 .$

Mer om

Denne oppgaven er om

Ekstremalpunkt

Vi sier at et punkt $x = a$ er et ekstremalpunkt for en funksjon $f (x)$ hvis det enten er et toppunkt eller bunnpunkt for funksjonen.

ekstremalpunkt

Toppunkt

Et toppunkt for en funksjon er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er større enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

toppunkt

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

Graf

graf

For flere forklaringer og eksempler på ekstremalpunkter, se artikkelen Topp- og bunnpunkter.

Oppgave 6 (6 poeng) Nettkode: E-4DHP

Figur 1 nedenfor viser grafen til funksjonen $f$ gitt ved

$f (x) = \frac{1}{x}, x \in [1, a]$

Vi dreier grafen til $f$ 360° om x-aksen. Vi får da fram et omdreiningslegeme som vist på figur 2.

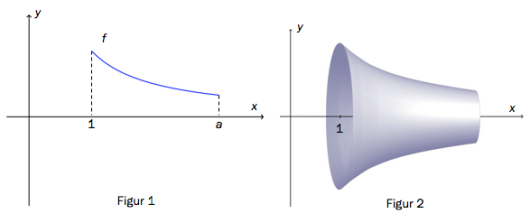
a)

Bestem volumet $V (a)$ av omdreiningslegemet.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Volumet av omdreiningslegemeet til en funksjon $f (x)$ kan skrives som et integral av sylindere med høyde $d x$ og grunnflate $π f (x)^{2}$ .

Ved å kutte omdreiningslegemet opp i uendelig mange, uendelig tynne sylindere med volum $π [f (x)]^{2} d x$ kan vi ved å integrere uttrykket fra $1$ til $a$ finne volumet av omdreiningslegemet. Med andre ord må vi ha $\begin{matrix} V (a) = \int_{1}^{a} π f (x)^{2} d x = π \int_{1}^{a} \frac{d x}{x^{2}} \end{matrix}$ og siden den deriverte av $\frac{- 1}{x}$ er $\frac{1}{x^{2}}$ må vi videre ha at $\begin{matrix} π \int_{1}^{a} \frac{d x}{x^{2}} = π {[- \frac{1}{x}]}_{1}^{a} = π (- \frac{1}{a} + \frac{1}{1}) = π (1 - \frac{1}{a}) . \end{matrix}$ Altså er volumet $V (a)$ av omdreiningslegemet lik $\begin{matrix} V (a) = π (1 - \frac{1}{a}) . \end{matrix}$

Svar: $\begin{matrix} V (a) = π (1 - \frac{1}{a}) \end{matrix}$

Mer om

Denne oppgaven er om

Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm³) og kubikkmeter (m³).

volum

Omdreiningslegeme

Et omdreiningslegeme (rotasjonslegeme) fremkommer ved at en plan figur dreier seg om en akse i figurens plan. Overflaten av et omdreiningslegeme er derfor en omdreiningsflate. Eksempler på omdreiningslegemer er kule, ellipsoide, sylinder og kjegle.

omdreiningslegeme

Pi (π)

$π$ er forholdet mellom sirkelens omkrets og diameter. Dette forholdet er alltid konstant og tilnærmet lik 3,14.

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

Derivasjon

En grenseoperasjon på en funksjon, som gir en ny funksjon, den deriverte til den opprinnelige. Funksjonsverdiene til den deriverte er stigningstallene til grafen til den opprinnelige funksjonen.

derivasjon

For flere forklaringer og eksempler på integrasjon, se artikkelen Volum av et omdreiningslegeme.

Visste du at

Ved å huske at vi kan skrive den deriverte til en funksjon $y$ med hensyn på $x$ som $d y / d x$ og at dette er de samme symbolene som fremkommer i et integral kan man komme langt. La oss for eksempel gjenoppdage formelen for omkretsen av en sirkel med radius $R$ . Punktene på denne sirkelen kan skrives $(R \cos θ, R \sin θ)$ for $θ \in [0, 2 π]$ . Vi ønsker å summere alle uendelig små biter $d s$ av sirkelens omkrets. De uendelig små bitene er rette linjer og tilfredsstiller derfor pythagoras læresetning $d s^{2} = d x^{2} + d y^{2}$ . Ved å dividere begge sider av likningen på $d θ^{2}$ finner vi da at $\begin{matrix} {(\frac{d s}{d θ})}^{2} = {(\frac{d x}{d θ})}^{2} + {(\frac{d y}{d θ})}^{2} \end{matrix}$ og derfor også $\begin{matrix} d s = \sqrt{{(\frac{d x}{d θ})}^{2} + {(\frac{d y}{d θ})}^{2}} d θ . \end{matrix}$ Omkretsen $O$ av en sirkel er da integralet $\begin{matrix} O = \int_{θ = 0}^{θ = 2 π} d s = \int_{0}^{2 π} \sqrt{{(\frac{d x}{d θ})}^{2} + {(\frac{d y}{d θ})}^{2}} d θ, \end{matrix}$ og siden $\frac{d x}{d θ} = (R \cos θ)' = - R \sin θ$ og $\frac{d y}{d θ} = (R \sin θ)' = R \cos θ$ må $\begin{matrix} \int_{0}^{2 π} \sqrt{{(\frac{d x}{d θ})}^{2} + {(\frac{d y}{d θ})}^{2}} d θ = \int_{0}^{2 π} \sqrt{R^{2} \sin^{2} θ + R^{2} \cos^{2} θ} d θ \\ = R \int_{0}^{2 π} \sqrt{\sin^{2} θ + \cos^{2} θ} d θ = R \int_{0}^{2 π} 1 d θ \\ = R (2 π - 0) = 2 π R, \end{matrix}$ som er det resultatet vi kjenner fra før.

b)

Bestem $\int_{1}^{a} f (x) dx$ . Omdreiningslegemet har overflateareal $O (a)$ . Forklar at $O (a) > \int_{1}^{a} f (x) dx$ .

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Integralet $\int_{1}^{a} f (x) d x$ er lik arealet under grafen til $f$ fra $x = 1$ til $x = a$ . Siden arealet $O (a)$ av omdreiningslegemet er overflaten til figuren som fremkommer av å rotere grafen til $f$ $360^{\circ}$ rundt $x$ -aksen må dette være større enn $\int_{1}^{a} f (x) d x$ . For hver tynne rektangel $f (x) d x$ i $\int_{1}^{a} f (x) d x$ må det tilhørende arealet i $O (a)$ faktisk være $2 π f (x) d x$ .

Først beregner vi

$\int_{1}^{a} f (x) d x = \int_{1}^{a} \frac{1}{x} d x = {|\ln (x)|}_{1}^{a} = \ln (a) - \ln (1) = \ln (a) .$

Hvis grafen til $f (x)$ over intervallet $[a, b]$ dreies om $x$ -aksen, får omdreiningslegemet areal lik

$\int_{a}^{b} 2 π f (x) \sqrt{1 + f^{'} {(x)}^{2}} d x .$

For vår graf, blir arealet av omdreiningslegemet

$O (a) = \int_{1}^{a} 2 π \cdot \frac{1}{x} \sqrt{1 + {(- \frac{1}{x^{2}})}^{2}} d x .$

Siden $2 π \sqrt{1 + {(- \frac{1}{x^{2}})}^{2}} > 1,$ må

$O (a) > \int_{1}^{a} \frac{1}{x} d x,$

som vi skulle vise.

Svar: $\begin{matrix} \int_{1}^{a} f (x) d x = \ln a \end{matrix}$

Mer om

Denne oppgaven er om

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

Omdreiningslegeme

omdreiningslegeme

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritme

Graf

graf

For flere forklaringer og eksempler på integrasjon, se artikkelen Bestemte integraler.

c)

Vi lar $a \to \infty$ . Det omdreiningslegemet vi da får, kalles Gabriels horn.

Bestem $\lim_{a \to \infty} O (a)$ og $\lim_{a \to \infty} V (a)$ dersom grenseverdiene eksisterer. Kommenter svarene.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker

Grenseverdiene $\lim_{a \to \infty} O (a)$ og $\lim_{a \to \infty} V (a)$ eksisterer dersom deres verdier er endelige tall.

Siden $\begin{matrix} O (a) > \int_{1}^{a} f (x) d x \end{matrix}$ kan ikke gresenverdien $\lim_{a \to \infty} O (a)$ eksistere dersom ikke grenseverdien $\begin{matrix} \lim_{a \to \infty} \int_{1}^{a} f (x) d x \end{matrix}$ eksisterer. Fra oppgave $b)$ vet vi at $\int_{1}^{a} f (x) d x = \ln a$ og siden

$\begin{matrix} \lim_{a \to \infty} \ln a = \infty, \end{matrix}$ må $\lim_{a \to \infty} O (a) = \infty$ . Dette betyr at grenseverdien ikke eksisterer.

Når det gjelder volumet av omdreiningslegemet, $V (a) = π (1 - \frac{1}{a})$ , finner vi $\begin{matrix} \lim_{a \to \infty} V (a) = \lim_{a \to \infty} π (1 - \frac{1}{a}) = π (1 - 0) = π, \end{matrix}$ som betyr at grenseverdien $\lim_{a \to \infty} V (a)$ eksisterer og har verdien $π$ . Vi har altså funnet ut at det i teoreien er mulig å bygge et legeme med uendelig stort areal, men med et endelig volum $π$ . Hvis både $x$ og $y$ måles i desimeter vil volumet måles i liter og arealet måles i kubikkdesimeter. Tenker vi på Gabriels horn vil det kreves uendelig mye maling for å male hele hornets innside, men for å fylle hele hornets innside vil man bare trenge $π$ liter maling.

Svar:

$\begin{matrix} \lim_{\to \infty} & \ln (a) = \infty \\ \lim_{\to \infty} & V (a) = π \end{matrix} \begin{matrix} (eksisterer ikke) \end{matrix}$

Mer om

Denne oppgaven er om

Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm³) og kubikkmeter (m³).

volum

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

Omdreiningslegeme

omdreiningslegeme

Pi (π)

$π$ er forholdet mellom sirkelens omkrets og diameter. Dette forholdet er alltid konstant og tilnærmet lik 3,14.

Grenseverdi

En uendelig tallfølge a₁, a₂, a₃, ...har grenseverdi A dersom vi kan få a_n så nær A vi vil ved å velge n stor nok.

grenseverdi

Integrasjon

Det motsatte av derivasjon. En grenseoperasjon på en funksjon som kan tolkes som arealet begrenset av grafen til funksjonen og x-aksen.

Se Integralregning

integrasjon

Logaritme

Logaritmen til et positivt tall n er den eksponenten som må brukes for å uttrykke n som en potens av et valgt fast tall, grunntall. Vanlige grunntall er e og 10.

Eksempel: log₁₀(1000) = 3 ettersom 10³ = 1000.

logaritme

For flere forklaringer og eksempler på grenseverdier, se artikkelen Grenseverdier.

REA3024 2014 Vår

Del 1

Del 2

Eksamensinformasjon

DEL 1 Uten hjelpemidler

Oppgave 1 (3 poeng) Nettkode: E-4DG6

a)

Løsningsforslag a)

Sinus

Cosinus

Derivasjon

b)

Løsningsforslag b)

Sinus

Cosinus

Eksponentialfunksjon

Derivasjon

Oppgave 2 (4 poeng) Nettkode: E-4DG9

a)

Løsningsforslag a)

Sinus

Cosinus

Derivasjon

Integrasjon

b)

Løsningsforslag b)

Logaritme

Integrasjon

Oppgave 3 (2 poeng) Nettkode: E-4DGC

Løsningsforslag

Vendepunkt

Eksponentialfunksjon

Graf

Derivasjon

Andrederiverte

Oppgave 4 (4 poeng) Nettkode: E-4DGE

a)

Løsningsforslag a)

Sum

Konvergens

Uendelige rekker

b)

Løsningsforslag b)

Konvergent tallfølge

Ligning

Oppgave 5 (5 poeng) Nettkode: E-4DGH

a)

Løsningsforslag a)

Vektor

Plan

Ligning

Punkt

b)

Løsningsforslag b)

Linje

Vektor

Normal

Plan

c)

Løsningsforslag c)

Skjæringspunkt

Linje

Ligning

Plan

Punkt

d)

Løsningsforslag d)

Alternative løsninger

Skjæringspunkt

Linje

Rett vinkel

Plan

Punkt

Cosinus

Oppgave 6 (4 poeng) Nettkode: E-4DGM

a)

Løsningsforslag a)

Sinus

Toppunkt

Bunnpunkt