Vendepunkt og vendetangent

 

På samme måte som at vi finner topp- og bunnpunktene ved å se på de

til $f\left(x\right)$, er vendepunktene blant de kritiske punktene til $f\text{'}\left(x\right)$. Vendepunktene er de punktene der veksthastigheten til grafen, altså $f\text{'}\left(x\right)$, er på sitt største eller minste.

For å finne vendepunkter i praksis, lager vi fortegnslinja til den annenderiverte $f\text{'}\text{'}\left(x\right)$. Ut i fra den kan man lese av direkte hvor vendepunktene til grafen er. Prosessen er helt parallell med å finne ekstremalpunkter. Det er verdt å merke seg at mange grafer ikke har noen vendepunkter i det hele tatt. Det enkleste eksemplet på en graf som har et vendepunkt, er dette:

Eksempel

Oppgave. Bestem vendepunktene til grafen til $f\left(x\right)=x^3$.
Løsning. Vi deriverer to ganger:

$f^{\prime }\left(x\right)=3x^2$, og

$f^{\prime \prime }\left(x\right)=6x$.

Fortegnslinja til $6x$ kan du prøve å tegne opp: Den avslører at krumningen til $f$ skifter fortegn i punktet $x=0$. Vi vet da at krumningen til $f$ skifter fra konkav til konveks i punktet, og grafen har et vendepunkt i punktet $x=0$.

Å finne vendetangenten:

For å finne vendetangenten finner vi først

til en funksjon i et punkt. Vi regner ut tangenten ved likningen under:

La $f\left(x\right)$ være to ganger deriverbar i et punkt $x=c$. Tangenten $t\left(x\right)$,  til $f$  i punktet $\left(c,f\left(c\right)\right)$  er da gitt ved:

            $t\left(x\right)=f\text{'}\left(c\right)\left(x-c\right)+f\left(c\right)$.

Hvis $c$ i tillegg er et vendepunkt for funksjonen, er $t\left(x\right)$ vendetangenten. Du kan lese mer om å finne tangenten til en kurve i artikkelen "Ettpunktformelen og likning for tangentlinjen" som du finner til høyre.

Eksempel

Oppgave. Finn vendepunktene og vendetangentene til grafen til funksjonen $f\left(x\right)=\frac{1}{36}{x}^4-\frac{1}{6}{x}^3+2$.
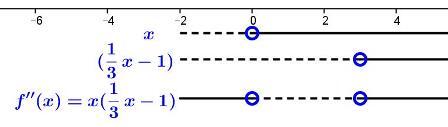
Løsning. Fra fortegnslinja til $f\text{'}\text{'}$ under ser vi at krumningen til f skifter i punktene $x=0$ og $x=3$. Grafen har derfor to vendepunkter, nemlig $(0,f(0\left)\right)=(0,2)$ og $(3,f(3\left)\right)=(3,-\frac{1}{4})$.

Vi finner vendetangentene ved å bruke formelen over.

Vi finner først den deriverte $f\text{'}\left(x\right)=\frac{1}{9}{x}^3-\frac{1}{2}{x}^2$.

Vi ser først på punktet $\left(0,f\left(0\right)\right)$:

Her er $f\text{'}\left(0\right)=0$ og dermed får vi

$t\left(x\right)=f\text{'}\left(c\right)\left(x-c\right)+f\left(c\right)=0\cdot \left(x-0\right)+2=2$

for $c=0$.

Vi ser nå på $\left(3,f\left(3\right)\right)=\left(3,-\frac{1}{4}\right)$:

Her er $f\text{'}\left(3\right)=-\frac{3}{2}$ og vi får:

$t\left(x\right)=f\text{'}\left(c\right)\left(x-c\right)+f\left(c\right)=-\frac{3}{2}\left(x-3\right)+\left(-\frac{1}{4}\right)=-\frac{3}{2}x+\frac{17}{4}$

for $c=3$.

 
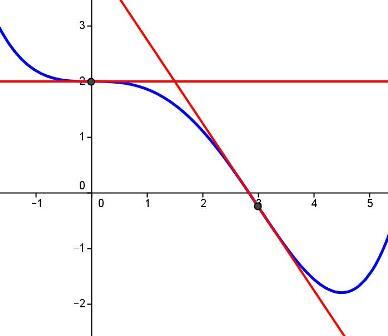
Figuren under viser grafen med de to vendetangentene. Legg merke til hvordan vendetangentene krysser grafen akkurat i tangeringspunktet.