Eksamensoppgavesettet er utarbeidet av Utdanningsdirektoratet. Avvik fra det originale eksamenssettet er eventuelle spesifiseringer og illustrasjoner. Løsningsforslagene i sin helhet er utarbeidet av matematikk.org.

Nettkoden som står til høyre for oppgavetittelen brukes i søkefeltet på www.matematikk.org for å åpne oppgaven og se utfyllende løsningsforslag.

Våre samarbeidspartnere:

MAT1011 2015 Vår

Del 1
Del 2
Eksamensinformasjon

Eksamenstid:

5 timer:
Del 1 skal leveres inn etter 2 timer.
Del 2 skal leveres inn senest etter 5 timer.

Hjelpemidler:

Del 1:

Vanlige skrivesaker, passer, linjal med centimetermål og vinkelmåler.

Del 2:

Alle hjelpemidler er tillatt, med unntak av Internett og andre verktøy som tillater kommunikasjon.

Framgangsmåte:
Del 1 har 10 oppgaver. Del 2 har 9 oppgaver.

Der oppgaveteksten ikke sier noe annet, kan du fritt velge framgangsmåte. Dersom oppgaven krever en bestemt løsningsmetode, kan en alternativ metode gi lav/noe uttelling.

Bruk av digitale verktøy som graftegner og regneark skal dokumenteres med utskrift eller gjennom en IKT-basert eksamen.

Veiledning om vurderingen:
Poeng i Del 1 og Del 2 er bare veiledende i vurderingen. Karakteren blir fastsatt etter en samlet vurdering. Det betyr at sensor vurderer i hvilken grad du

viser regneferdigheter og matematisk forståelse
gjennomfører logiske resonnementer
ser sammenhenger i faget, er oppfinnsom og kan ta i bruk fagkunnskap i nye situasjoner
kan bruke hensiktsmessige hjelpemidler
forklarer framgangsmåter og begrunner svar
skriver oversiktlig og er nøyaktig med utregninger, benevninger, tabeller og grafiske framstillinger
vurderer om svar er rimelige

Andre opplysninger:

Kilder for bilder, tegninger osv.

FN: (http://www.dn.no, 5.07.2016)
Andre bilder, tegninger og grafiske framstillinger: Utdanningsdirektoratet

DEL 1 Uten hjelpemidler

Oppgave 1 (1 poeng) Nettkode: E-4AZI

Skriv som prosent

a)

$0, 451$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker:

Tallet er på

Desimaltall

Desimaltall er tall som inneholder komma.

Eksempel: 2,34 og 18,001

Sifrene som følger etter komma, kalles desimaler.

desimalform

, så vi kan

Multiplikasjon

Å multiplisere er det samme som gjentatt addisjon, ofte kalt "ganging".

Regneoperasjonen 3 · 4 = 12 kalles en multiplikasjon, og sier at vi skal legge sammen tallet 3 fire ganger, eller at vi skal ta tallet 4 og addere dette med seg selv 3 ganger.

Produktet blir det samme, uansett hvilken rekkefølge faktorene kommer i.

Eksempel: 3 · 4 = 12 og 4 · 3 = 12

Tallene 3 og 4 kalles faktorer, og resultatet kalles et produkt.
Mellom faktorene skrives multiplikasjonstegn (·).

multiplisere

med 100. Tall på desimalform er

Prosentfaktor

En prosentfaktor er et prosenttall skrevet om til et desimaltall.

Eksempel: 32 % blir skrevet som 0,32 når det skal skrives som en prosentfaktor.

prosentfaktoren

av det vi får når vi multipliserer med

100 %

Vi vet at $1 = 100 %$ , så alt vi trenger å gjøre for å konvertere desimaltall til prosent er å multiplisere med $100 %$ . Dette tilsvarer å flytte kommategnet to hakk til høyre: $0, 451 = 0, 451 \cdot 1 = 0, 451 \cdot 100 % = 45, 1 % .$

Svar: $45, 1 %$

Mer om:

Denne oppgaven er om se

Prosent

Prosent betyr hundredel og skrives %.

Eksempel: Hvor mange prosent er 1 av 4? $\frac{1}{4} = \frac{1 \cdot 25}{4 \cdot 25} = \frac{25}{100} = 25 %$ .

prosent

Prosentfaktor

En prosentfaktor er et prosenttall skrevet om til et desimaltall.

Eksempel: 32 % blir skrevet som 0,32 når det skal skrives som en prosentfaktor.

prosentfaktor

Desimaltall

Desimaltall er tall som inneholder komma.

Eksempel: 2,34 og 18,001

Sifrene som følger etter komma, kalles desimaler.

desimaltall

For flere eksempler og forklaringer se artikkelen Hva er prosent? i lynkurset Prosent.

For å øve mer, se oppgavesettet om prosentregning i Treningsleieren.

b)

$\frac{5}{25}$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker:

Det står 25 i

Nevner

Tallet som står under brøkstreken i en brøk.
Nevneren forteller hvor mange like deler det hele er delt opp i.

Eksempel : $\frac{3}{7}$ . Tallet 7 er nevneren.

nevneren

, så vi kan

Multiplikasjon

multiplisere

opp for å få 100 i stedet.

“Prosent” betyr “del av hundre”. Eksempelvis betyr $2 %$ det samme som $\frac{2}{100}$ . I vår oppgave kan vi få tallet på den samme formen ved å multiplisere med 4 over og under brøkstreken. $\frac{5}{25} = \frac{5 \cdot 4}{25 \cdot 4} = \frac{20}{100} = 20 %$ Vi kan også gjøre det på samme måte som forrige oppgave, ved å se at $\frac{5}{25} = 0, 2 = 20 %$ .

Svar: $20 %$

Mer om:

Denne oppgaven er om se

Prosent

Prosent betyr hundredel og skrives %.

Eksempel: Hvor mange prosent er 1 av 4? $\frac{1}{4} = \frac{1 \cdot 25}{4 \cdot 25} = \frac{25}{100} = 25 %$ .

Prosent

Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.

Brøk kan sees som et tall på tallinja eller som del av en mengde.

brøk

og og

Desimaltall

Desimaltall er tall som inneholder komma.

Eksempel: 2,34 og 18,001

Sifrene som følger etter komma, kalles desimaler.

Desimaltall

For flere eksempler og forklaringer se artikkelen Hva er prosent? i lynkurset Prosent.

For å øve mer, se oppgavesettet om prosentregning i Treningsleieren.

Oppgave 2 (2 poeng) Nettkode: E-4AZM

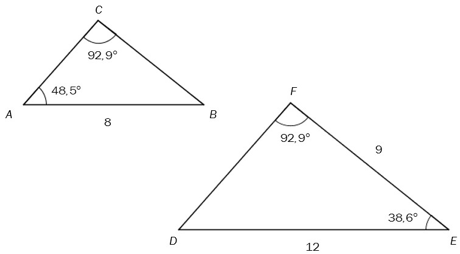
a)

Forklar at de to trekantene ovenfor er formlike.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker:

Vi ser at $∠ C = ∠ F$ . Det ser også ut til at $∠ A = ∠ D$ og $∠ B = ∠ E$ . Vi kan finne de ukjente vinklene i begge

Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.

trekantene

ved å bruke at

Vinkelsum

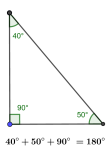
Summen av alle vinklene i en mangekant.

Vinkelsummen i en trekant er alltid 180 grader og vinkelsummen i en firkant er alltid 360 grader.

vinkelsummen i en trekant

180^{\circ}

Denne oppgaven handler om vinkler i trekanter, og da skal vi ofte bruke at vinkelsummen i trekanter er $180^{\circ}$ .

Svar:

To trekanter er formlike hvis de har parvis likestore vinkler, så vi må vise at

∠ A = ∠ D

∠ B = ∠ E

∠ C = ∠ F

. Tegningen viser at

∠ C = ∠ F = 92, 9^{\circ}

. Summen av alle vinklene i en trekant er alltid lik

180^{\circ}

, så i

Λ B D E

har vi at

∠ D + ∠ E + ∠ F = 180^{\circ} .

I tegningen ser vi at

∠ F = 92, 9^{\circ}

og at

∠ E = 38, 6^{\circ}

. Hvis vi setter dette inn i likningen

∠ D + ∠ E + ∠ F = 180^{\circ}

, får vi at

∠ D + 38, 6^{\circ} + 92, 9^{\circ} = 180^{\circ},

eller med andre ord,

∠ D + 131, 5^{\circ} = 180^{\circ} .

Vi løser likningen over med hensyn på

∠ D

ved å trekke fra

131, 5^{\circ}

på hver side av likhetstegnet, og da får vi

∠ D = 180^{\circ} - 131, 5^{\circ} .

Vi legger sammen gradene på høyre side og får til slutt

∠ D = 48, 5^{\circ} .

Vi vet allerede at

∠ A = 48, 5^{\circ}

, så

∠ A = ∠ D

. Nå kan vi faktisk si oss ferdige, hvis vi merker oss at kun to vinkler må være parvis like store for at vi skal ha formlike trekanter. Vi kan sjekke at dette stemmer ved å bruke at vinkelsummen er lik

180^{\circ}

i den første trekanten. Som før må vi ha at

∠ A + ∠ B + ∠ C = 180^{\circ},

så

∠ B = 180^{\circ} - 48, 5^{\circ} - 92, 9^{\circ} .

Vi legger sammen gradene på høyre side og får

∠ B = 38, 6^{\circ};

dermed er også

∠ B = ∠ E

. Nå har vi funnet ut at de to trekantene har parvis like store vinkler, så trekantene er formlike.

Mer om:

Denne oppgaven er om

Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.

trekant

Toppvinkler

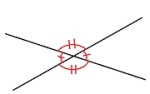
Når to rette linjer skjærer hverandre, dannes to par like store vinkler. Et slikt par kalles toppvinkler.

toppvinkler

Vinkelsum

Summen av alle vinklene i en mangekant.

Vinkelsummen i en trekant er alltid 180 grader og vinkelsummen i en firkant er alltid 360 grader.

vinkelsummen i en trekant

Formlike trekanter

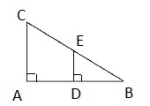
To trekanter er formlike hvis de har parvis like store vinkler.

Eksempel: $Δ A B C \sim Δ D B E$ , det leses trekant ABC er formlik med trekant DBE.

formlike trekanter

For flere eksempler og forklaringer se artikkelen Formlikhet og kongruens.

For å øve mer, se oppgavesettet om formlikhet og kongruens i Treningsleieren.

b)

Bestem lengden av siden BC ved regning.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker:

Formlike trekanter

To trekanter er formlike hvis de har parvis like store vinkler.

Eksempel: $Δ A B C \sim Δ D B E$ , det leses trekant ABC er formlik med trekant DBE.

Formlike trekanter

har parvis like store vinkler, men de har også egenskapen at

Proporsjon

Proporsjon betyr at to forhold er like.

Eksempel: a forholder seg til b som c forholder seg til d, $\frac{a}{b} = \frac{c}{d}$

forholdet

mellom lengdene til samsvarende sider er det samme. Vi vet at trekantene er formlike, så vi kan bruke lengden til

E F

til å regne ut lengden til

B C

Fordi trekantene er formlike er forholdet mellom lengdene til tilsvarende sider det samme. For eksempel er $\frac{A B}{D E}$ det samme som $\frac{B C}{E F}$ . Dette er nyttig for oss, siden vi allerede vet lengdene til $A B$ , $D E$ og $E F$ ; de er henholdsvis 8, 12 og 9. Vi kan sette dette opp som en likning: $\frac{A B}{D E} = \frac{B C}{E F} .$ Setter vi inn verdiene vi har fått oppgitt, får vi $\frac{8}{12} = \frac{B C}{9} .$ Vi multipliserer med 9 på begge sider av likhetstegnet, og forkorter på høyre side. $\frac{8}{12} \cdot 9 = \frac{B C}{9} \cdot 9 .$ Vi regner ut at $\frac{8}{12} \cdot 9 = 6$ og forkorter $\frac{B C}{9} \cdot 9$ til $B C$ . Til slutt får vi $B C = 6 .$

Svar: Lengden til $B C$ er 6.

Mer om

Denne oppgaven er om

Formlike trekanter

To trekanter er formlike hvis de har parvis like store vinkler.

Eksempel: $Δ A B C \sim Δ D B E$ , det leses trekant ABC er formlik med trekant DBE.

formlike trekanter

Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.

trekanter

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likninger

For flere eksempler og forklaringer på formlike trekanter og trekanter generelt, se artikkelenFormlike Trekanter, og for likninger og hvordan å løse dem, se lynkurset Likninger.

For å øve mer, se oppgavesettet om formlike trekanter i Treningsleieren.

Oppgave 3 (2 poeng) Nettkode: E-4AZP

Et vindu har form som et rektangel. Vinduet er 6 dm bredt og 7 dm høyt.

Gjør beregninger og avgjør om det er mulig å få en kvadratisk plate med sider 9 dm inn gjennom vinduet.

Løs oppgaven her

Løsningsforslag

Jeg tenker:

I utgangspunktet ser det ikke mulig ut å få rektangelet gjennom vinduet, men det kan være mulig hvis vi holder

Kvadrat

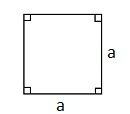
En firkant der alle sider er like lange og alle vinkler 90°.

kvadratet

på skrå.

Hvis vi holder kvadratet på skrå slik at det ligger på diagonalen til vinduet før vi prøver å ta det gjennom vinduet, er det mulig at vi får plass. Hvis vi skal få plass, må i så fall diagonalen på vinduet være lengre enn sidekantene til kvadratet, altså større enn 9 dm. La $x$ være lengden til diagonalen, slik bildet under viser.

Siden alle hjørnevinklene i et rektangel er $90^{\circ}$ , er trekanten under en rettvinklet trekant.

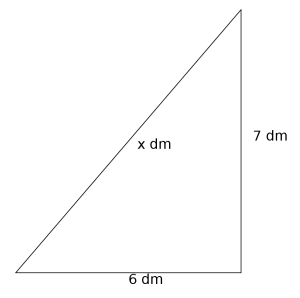
Dermed kan vi bruke

Pytagoras læresetning

Pytagoras læresetning sier at:

Arealet av kvadratet utspent av hypotenusen i en rettvinklet trekant er lik summen av arealene til kvadratene utspent av katetene.

Hvis lengden av katetene er a og b, og lengden av hypotenusen er c, har vi denne sammenhengen : $a^{2} + b^{2} = c^{2}$

Setningen kan brukes til å finne lengden til en side i en trekant.

Pytagoras’ setning

, som sier at

a^{2} = b^{2} + c^{2},

der

a

er lengden til trekantens hypotenus, og

b

c

er lengdene til katetene. I vårt tilfelle er

a = x

dm, altså den ukjente hypotenusen, mens

b

c

er henholdsvis 6 dm og 7 dm. Vi setter dette inn i

a^{2} = b^{2} + c^{2},

og får

x^{2} = 6^{2} + 7^{2} .

Vi regner ut høyre side over.

6^{2} + 7^{2} = 6 \cdot 6 + 7 \cdot 7 = 36 + 49 = 85 .

Dette betyr at

x^{2} = 85 .

Her kunne vi ha regnet ut

x

ved å finne kvadratroten av 85, men det eneste vi egentlig trenger å vite om

x

, er om den er større eller mindre enn 9. Siden

9^{2} = 9 \cdot 9 = 81 < 85

, må

x

være mindre enn 9, så kvadratet vil få plass gjennom vinduet.

Svar: Ja, det er mulig, siden diagonalen i vinduet er lengere enn 9 dm.

Mer om:

Denne oppgaven er om

Kvadrat

En firkant der alle sider er like lange og alle vinkler 90°.

kvadrat

Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.

trekant

Pytagoras læresetning

For flere eksempler og forklaringer se artikkelen om Pytagoras læresetning i Geometri - areal og volum.

For å øve mer, se oppgavesettet om Pytagoras læresetning i Treningsleieren.

Visste du at:

Pytagoras’ læresetning er et av de eldste matematiske resultatene vi vet om, og flere gamle sivilisasjoner har kommet fram til setningen uavhengige av hverandre. Setningen har blitt bevist på mange forskjellige måter; Euklid hadde en meget komplisert framgangsmåte, mens den amerikanske presidenten James Garfield beviste det ved å regne ut arealet av et spesielt trapes. Setningen kan også bevises ved hjelp av figuren under – klarer du det?

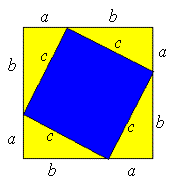
Et forslag står nederst i artikkelen Pytagoras' setning.

Oppgave 4 (2 poeng) Nettkode: E-4AZX

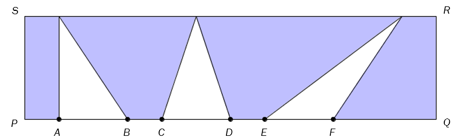
Figuren ovenfor viser et rektangel $P Q R S$ . $P Q = 12$ cm, $Q R = 3$ cm og

$A B = C D = E F = 2$ cm

Bestem arealet av det blå området

Løs oppgaven her

Løsningsforslag

Jeg tenker:

Vi har høyden og grunnlinjen til alle

Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.

trekantene

, så vi kan regne ut

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

arealet

til det store

Rektangel

Et rektangel er en firkant der sidene er parvis like lange og alle vinklene er 90°.

Areal: $A = a b$

Omkrets: $O = 2 a + 2 b$

rektangelet

og trekke fra arealet til trekantene.

Arealet til det blå området er gitt ved arealet til hele rektangelet $P Q R S$ minus arealene til de tre mindre trekantene. Vi skal regne ut arealet til alle figurene for seg, og deretter regne ut arealet til det blå området.

Grunnlinjen til rektangelet har lengde $P Q = 12 cm$ , og høyden er $Q R = 3 cm$ . Arealet til rektangelet blir da $P Q \cdot Q R = 12 cm \cdot 3 cm = 36 {cm}^{2} .$

Vi anser sideflatene til trekantene som ligger på linjestykket $P Q$ til å være grunnlinje. Med dette valget har alle trekantene lik grunnlinje, så selv om de tre trekantene ser ganske forskjellige ut, har alle tre likt areal. Grunnlinjen er $A B = C D = E F = 2$ cm og høyden er 3 cm, så arealet av hvert kvadrat er $\frac{1}{2} \cdot 2 cm \cdot 3 cm = 3 {cm}^{2} .$

Arealet til det blå området blir nå $\begin{matrix} 36 {cm}^{2} - 3 {cm}^{2} - 3 {cm}^{2} - 3 {cm}^{2} \\ = 36 {cm}^{2} - 3 \cdot 3 {cm}^{2} = 36 {cm}^{2} - 9 {cm}^{2} = 27 {cm}^{2} . \end{matrix}$

Svar: Arealet av det blå området er $27 {cm}^{2}$ .

Mer om:

Denne oppgaven er om

Rektangel

Et rektangel er en firkant der sidene er parvis like lange og alle vinklene er 90°.

Areal: $A = a b$

Omkrets: $O = 2 a + 2 b$

rektangel

Trekant

En trekant er en todimensjonal figur med tre hjørner og tre sidekanter.

trekant

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

For flere eksempler og forklaringer se artikklene Et rektangel og En trekant i lynkurset Geometri - areal og volum.

For å øve mer, se oppgavesettet areal i Treningsleieren.

Oppgave 5 (4 poeng) Nettkode: E-4B03

Funksjonen $f$ er gitt ved

$f (x) = x^{2} + 2 x - 3$

a)

Skriv av verditabellen nedenfor i besvarelsen din, og fyll inn tallene som mangler.

$x$	$- 4$	$- 3$	$- 2$	$- 1$	$0$	$1$	$2$
$f (x)$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker:

Vi må sette opp en tabell med $x$ -verdiene, og fylle inn det vi får når vi setter verdiene inn i funksjonsuttrykket $f (x)$ .

Den eneste måten å løse dette på er å sette inn de oppgitte $x$ -verdiene inn for $x$ i funksjonsuttrykket $x^{2} + 2 x - 3$ . Vi starter med $x = - 4$ , og vi må huske at når vi setter inn negative tall i et funksjonsuttrykk, så skal vi ha parenteser rundt tallet. På denne måten unngår vi fortegnsfeil. Med dette i tankene setter vi inn $x = - 4$ funksjonsuttrykket, og får $\begin{matrix} f (- 4) & = (- 4)^{2} + 2 \cdot (- 4) - 3 \\ = (- 4) \cdot (- 4) + 2 \cdot (- 4) - 3 . \end{matrix}$ Husk at når vi multipliserer to negative tall får vi et positivt, så da får vi $f (- 4) = 16 - 8 - 3 = 5 .$ Vi setter resultatet inn i skjemaet:

$x$	$- 4$	$- 3$	$- 2$	$- 1$	$0$	$1$	$2$
$f (x)$	$5$

Vi gjør det samme for $x = - 3$ , og får $\begin{matrix} f (- 3) & = (- 3)^{2} + 2 \cdot (- 3) - 3 \\ = 9 - 6 - 3 = 0 . \end{matrix}$ Vi fortsetter, og får $\begin{matrix} f (- 2) & = 4 - 4 - 3 = - 3, \\ f (- 1) & = 1 - 2 - 3 = - 4, \\ f (0) & = 0 + 0 - 3 = - 3, \\ f (1) & = 1 + 2 - 3 = 0 og \\ f (2) & = 4 + 4 - 3 = 5, \end{matrix}$ så svaret blir

$x$	$- 4$	$- 3$	$- 2$	$- 1$	$0$	$1$	$2$
$f (x)$	$5$	$0$	$- 3$	$- 4$	$- 3$	$0$	$5$

Svar:

$x$	$- 4$	$- 3$	$- 2$	$- 1$	$0$	$1$	$2$
$f (x)$	$5$	$0$	$- 3$	$- 4$	$- 3$	$0$	$5$

Mer om:

Denne oppgaven er om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

Andregradsuttrykk

Et uttrykk på formen $a x^{2} + b x + c$ , hvor $x$ er den størrelsen som varierer, og $a, b$ og $c$ er konstante tall.

andregradsuttrykk

For flere eksempler og forklaringer se artikkelen Andregradsfunksjoner og Hvorfor ser grafen ut som den gjør? i lynkurset Funksjoner (del I). For enda mer om funksjoner se lynkurset Funksjoner (del II).

For å øve mer, se oppgavesettet om kvadratiske funksjoner i Treningsleieren.

b)

Tegn grafen til f for $- 4 \leq x \leq 2$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker:

Vi må tegne et

Koordinatsystem

Et koordinatsystem i planet består av to akser, x-aksen og y-aksen. Aksene står vinkelrett på hverandre. x-aksen er horisontal og y-aksen er vertikal. Punktet der aksene krysser kalles for origo. Koordinatsystemet gir oss muligheten til å presentere punkter i planet i form av to tallverdier (x,y). Origo har koordinatene (0,0).

koordinatsystem

med punktene fra verditabellen.

Først må vi tegne et koordinatsystem. Vi skal tegne grafen når $x$ er mellom -4 og 2; derfor tegner vi $x$ -aksen for disse verdiene. Fra verditabellen vet vi at funksjonen varierer mellom -4 og 5, og vi tegner $y$ -aksen mellom disse verdiene. Vi setter navn på aksene for å vise hvilke variabler de representerer, og merker jevnlig av hvor vi er på aksene.

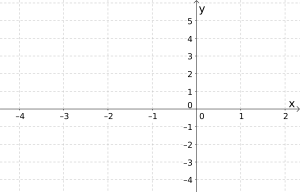
Vi skal tegne grafen til funksjonen, og ut i fra verditabellen vet vi cirka hvordan grafen går. Derfor markerer vi punkter på plassene som verditabellen indikerer. For eksempel sier tabellen at når $x = - 4$ , så er $y = f (- 4) = 5$ , så vi må markere punktet $(- 4, 5)$ i koordinatsystemet. Vi gjør det samme for punktene $(- 3, 0)$ , $(- 2, - 3)$ , $(- 1, - 4)$ , $(0, - 3)$ , $(1, 0)$ og $(2, 5)$ .

Nå kan vi se cirka hvordan grafen går, og vi må prøve å fylle inn grafen der vi ikke har punktene å støtte oss på. Én måte å gjøre det på er å tegne rette streker mellom punktene, men dette gjør ikke funksjonen like pen som den egentlig er. Helst skal vi prøve å glatte ut kantene så mye som mulig. Under er et bilde av hvordan det ser ut når man tegner rette streker i kontrast til hvordan grafen egentlig skal tegnes.

Her har vi tegnet rette linjer mellom punktene.

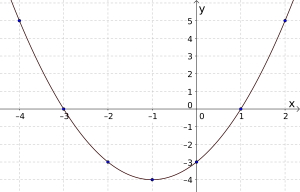
Her er den egentlige grafen tegnet. Linjene er mye glattere.

Svar:

Mer om:

Denne oppgaven er om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjoner

Graf

En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.

graf

For flere eksempler og forklaringer se Funksjonsgrafer for andregradsfunksjoner og Hvorfor ser grafen ut som den gjør? i lynkurset Funksjoner (del I). For enda mer om funksjoner se lynkurset Funksjoner.

For å øve mer, se oppgavesettet kvadratiske funksjoner i Treningsleieren.

Oppgave 6 (3 poeng) Nettkode: E-4B0B

Tenk deg at du har ni flasker med smoothie i kjøleskapet, to «Surf», tre «Jump» og fire

«Catch». Du tar tilfeldig to flasker.

a)

Bestem sannsynligheten for at du ikke tar en «Jump»-smoothie.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker:

Sannsynlighet

Sannsynligheten for noe forteller hvor sikkert eller usikkert det er at en hendelse skal skje.
En sannsynlighet er minst 0 og maks 1.

Sannsynlighet 0 betyr at en hendelse helt sikkert ikke skjer.
Sannsynlighet 1 betyr at en hendelse helt sikkert skjer.

Når du kaster mynt og kron, er sannsynligheten for å få mynt 0,5 og kron 0,5.

Sannsynligheten for å få mynt eller kron er 1.

Sannsynligheten

for å ikke ta en “Jump”-smoothie er lik sannsynligheten for å ta en hvilken som helst annen smoothie.

Vi har totalt ni flasker smoothie, og tre av dem er av type “Jump”. Det betyr at de seks resterende ikke er av type “Jump”. Hvis vi lar smoothier som er av type “Jump” betegnes med $J$ og de resterende med $X$ , kan vi representere situasjonen slik: $X X X X X X J J J$ Vi skal trekke ut to tilfeldige av disse, og skal bestemme sannsynligheten for at ingen av dem er en “Jump”-smoothie. Det er det samme som å bestemme sannsynligheten for at begge smoothiene vi trekker ut, er blant de seks som ikke er av typen “Jump”. Første gang vi trekker, er sannsynligheten for å trekke en smoothie som ikke er av type “Jump” (det vil si, sannsynligheten for å trekke en $X$ ut av bokstavene over) lik $\frac{6}{9}$ . Situasjonen etter vi har trukket en “Jump”-smoothie er slik: $X X X X X J J J$ Vi har altså fjernet en $X$ . Når vi trekker den neste, vil da sannsynligheten for at vi ikke trekker en “Jump”-smoothie (det vil si, sannsynligheten for å trekke en $X$ ) lik $\frac{5}{8}$ .

La oss oppsummere: Sannsynligheten for å ikke trekke en “Jump”-smoothie første gang, er $\frac{6}{9}$ . Hvis vi ikke trekker en “Jump”-smoothie første gang, vil sannsynligheten for at vi ikke trekker en den andre gangen være $\frac{5}{8}$ . Sannsynligheten for at vi ikke trekker en “Jump”-smoothie overhodet er lik sannsynligheten for at begge disse hendelsene inntreffer, så vi vil få riktig svar om vi multipliserer sammen de to sannsynlighetene. Svaret blir derfor $\frac{6}{9} \cdot \frac{5}{8} = \frac{5}{12}$ .

Svar: Sannsynligheten for at vi ikke tar en “Jump”-smoothie er $\frac{5}{12}$ .

Mer om:

Denne oppgaven er om

Sannsynlighet

sannsynlighet

For flere eksempler og forklaringer se artikkelen Sannsynlighet ved komplementære hendelser i lynkurset Sannsynlighet.

For å øve mer, se oppgavesettet om sannsynlighet i Treningsleieren.

b)

Bestem sannsynligheten for at du tar én «Surf»- og én «Catch»-smoothie.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker:

Det er to mulige måter trekke trekke én “Surf”-smoothie og én “Catch”-smoothie. Den ene måten er å trekke “Surf”-smoothien først og “Catch”-smoothien etterpå, men vi kan også trekke dem i motsatt rekkefølge.

Vi må ta hensyn til at det er to mulige måter å trekke én “Surf”- og én “Catch”-smoothie.

La $S, J$ og $C$ betegne henholdsvis “Surf”-smoothier, “Jump”-smoothier og “Catch”-smoothier. Situasjonen kan representeres slik: $S S J J J C C C C$ Sannsynligheten for å trekke en “Surf”-smoothie første gangen er $\frac{2}{9}$ , siden vi har 2 “Surf”-smoothier blant 9 smoothier. I så fall er vi i følgende situasjon: $S J J J C C C C$ Sannsynligheten for å trekke en “Catch”-smoothie nå er derfor $\frac{4}{8}$ , så til slutt blir sannsynligheten for å først trekke en “Surf”-smoothie og deretter en “Catch”-smoothie lik $\frac{2}{9} \cdot \frac{4}{8} = \frac{1}{9}$ .

På tilsvarende måte kan vi regne ut at sannsynligheten for først å trekke en “Catch”-smoothie og deretter en “Surf”-smoothie lik $\frac{4}{9} \cdot \frac{2}{8} = \frac{1}{9}$ . Vi vil vite sannsynligheten for at én av disse hendelsene inntreffer. Siden hendelsene er uavhengige, blir svaret $\frac{1}{9} + \frac{1}{9} = \frac{2}{9}$ .

Svar: Sannsynligheten for å trekke én “Catch”-smoothie og én “Surf”-smoothie er lik $\frac{2}{9}$ .

Mer om:

Denne oppgaven er om

Sannsynlighet

sannsynlighet

Sannsynlighet med tilbakelegging

Fra et utvalg trekker vi en tilfeldig gjenstand. Hvis vi legger tilbake gjenstanden før vi trekker neste, sier vi at forsøket er gjort med tilbakelegging.

Eksempel: Du skal trekke to kuler fra ei eske. Det er 5 røde og 5 blå kuler i eska. Du trekker en kule og noterer resultatet. Før du trekker neste kule, må den første legges tilbake i eska. Du har fortsatt 5 røde og 5 blå kuler i eska.

utvalg med tilbakelegging

Produktsetningen

Produktsetningen sier at $P (A \cap B) = P (A | B) \cdot P (B)$ , hvor $P (A | B)$ er den sannsynligheten for at A inntreffer gitt B.

produktsetningen

Addisjonssetningen

Sannsynligheten for unionen av flere hendelser kan regnes ut ved å legge sammen sannsynlighetene for hver enkelt hendelse, og så trekke fra sannsynligheten for alle snitt av hendelsene.

$P (A \cup B) = P (A) + P (B) - P (A \cap B)$

addisjonssetningen

For flere eksempler og forklaringer se artiklene Betinget sannsynlighet og produktrsetningen og Addisjonssetningen lynkurset Sannsynlighet (del II).

For å øve mer, se oppgavesettet produktsetningen og addisjonssetningen i Treningsleieren.

Oppgave 7 (2 poeng) Nettkode: E-4B0F

I 2012 kostet en vare 6 kroner. Indeksen for varen var da 120. I 2014 var indeksen for varen 160.

Hvor mye skulle varen ha kostet i 2014 dersom prisen hadde fulgt indeksen?

Løs oppgaven her

Løsningsforslag

Jeg tenker:

Forholdet mellom

Konsumprisindeks

Konsumprisindeks (KPI) er en indeks som viser endringer i prisene på varer og tjenester som kjøpes av husholdninger, sammenlignet med et basisår. De varer og tjenester som utgjør det meste av husholdningsbudsjettet, tillegges størst vekt.

(hentet fra http://snl.no/konsumprisindeks)

indeks

og pris er

Konstant

En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.

Eksempel: $A = π r^{2}$ , $π$ er en konstant og $r$ er en variabel.

Se Variabel

konstant

, og vi kan finne prisen ut i fra dette.

Forholdet mellom prisen til et produkt og produktets indeks er konstant. I vårt tilfelle betyr dette at $\frac{indeks i 2012}{pris i 2012} = \frac{indeks i 2014}{pris i 2014} .$ La $x$ betegne prisen i 2014. Oppgaveteksten gir oss informasjon om indeks i 2012, pris i 2012 og indeks i 2014, og om vi setter dette inn i $\frac{indeks i 2012}{pris i 2012} = \frac{indeks i 2014}{pris i 2014}$ får vi $\frac{120}{6} = \frac{160}{x} .$ Vi vil finne et tall $x$ som gjør at dette stemmer. Merk først at $\frac{120}{6} = \frac{6 \cdot 20}{6} = 20$ , så vi kan skrive likningen $\frac{indeks i 2012}{pris i 2012} = \frac{indeks i 2014}{pris i 2014}$ som $20 = \frac{160}{x} .$ Vi har en $x$ i nevneren på høyre side. Dette er vanskelig å jobbe med, så vi multipliserer med $x$ på begge sider av likhetstegnet. $20 \cdot x = \frac{160}{x} \cdot x$ Nå kan vi forkorte høyre side, og vi har at $20 x = 160,$ så vi har fått $x$ opp fra nevneren. For å få $x$ til å stå alene på venstre side av likhetstegnet, dividerer vi med 20 på begge sider. $\frac{20 x}{20} = \frac{160}{20}$ Vi ser at $\frac{20 x}{20} = x$ og $\frac{160}{20} = 8$ , så likningen over gir $x = 8$ . Altså skulle varen ha kostet 8 kroner i 2014, dersom prisen hadde fulgt indeksen.

Vi merker oss en liten ting som kan gjøre utregningene raskere. I likningen $\frac{indeks i 2012}{pris i 2012} = \frac{indeks i 2014}{pris i 2014}$ , så har vi to brøker som er like hverandre. Den ukjente variabelen $x$ er i nevneren, og det gir litt mer regning enn om den hadde vært i telleren. Det har seg slik at hvis to brøker er like hverandre, så er også de omvendte brøkene like hverandre (så sant ingen av tellerene er 0), så vi kunne like godt ha løst likningen $\frac{6}{120} = \frac{x}{160}$ og fått $x = \frac{6}{120} \cdot 160 = 8,$ akkurat som over.

Svar: Varen skulle ha kostet 8 kroner i 2014 dersom prisen hadde fulgt indeksen.

Mer om:

Denne oppgaven er om

Konsumprisindeks

(hentet fra http://snl.no/konsumprisindeks)

konsumprisindeks

I Ofte stilte spørsmål har Orakelet forklart hva konsumprisindeks er. Lynkurset om konsumprisindeks er under utarbeidelsen og kommer snart.

Oppgave 8 (3 poeng) Nettkode: E-4B0J

En formel er gitt ved

$s = v_{0} \cdot t + \frac{1}{2} \cdot a \cdot t^{2}$

a)

Bestem $s$ når $v_{0} = 0, t = 8 og a = 10$

Løs oppgaven her

Løsningsforslag a)

Jeg tenker:

Vi må sette inn verdiene vi har fått oppgitt og regne ut verdien for $s$ .

Vi har fått oppgitt en formel for $s$ med mange forskjellige ukjente, men vi har fått vite hvilke verdier de ukjente har. Det eneste vi trenger å gjøre er å sette inn det vi vet, og så regne ut. Vi setter inn $v_{0} = 0$ , $t = 8$ og $a = 10$ : $\begin{matrix} s & = v_{0} \cdot t + \frac{1}{2} \cdot a \cdot t^{2} \\ = 0 \cdot 8 + \frac{1}{2} \cdot 10 \cdot 8^{2} . \end{matrix}$ Alt som multipliserers med 0 blir 0, og $8^{2}$ betyr $8 \cdot 8$ , så dette blir $s = \frac{1}{2} \cdot 10 \cdot 8 \cdot 8 = 5 \cdot 8 \cdot 8 = 5 \cdot 64 = 320 .$

Svar: Vi får at $s = 320$ .

Mer om:

Denne oppgaven er om

Vei, fart og tid

Sammenhengen er v =s/t , der vei = s, fart = v og tid = t .

vei, fart og tid

For flere eksempler og forklaringer se artikkelen Målingsforhold.

For å øve mer, se oppgavesettet om vei, fart og tid i Treningsleieren.

Visste du at:

Likningen $s = v_{0} \cdot t + \frac{1}{2} \cdot a \cdot t^{2}$ sier faktisk hvor langt et objekt har beveget seg etter $t$ sekunder, hvis objektet starter med hastigheten $v_{0}$ m/s og har akselerasjonen $a$ m/s $^{2}$ . Det vi har regnet ut er at hvis et objekt starter i ro (altså har startshastighet 0 m/s) og akselererer med 10 m/s $^{2}$ , vil objektet ha reist 320 meter på 8 sekunder.

b)

Bestem $a$ når $v_{0} = 20, t = 4 og s = 144$

Løs oppgaven her

Løsningsforslag b)

Jeg tenker:

Vi må sette inn informasjonen vi har fått og løse

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likningen

for

a

Vi starter igjen med å sette inn all informasjonen vi har fått. $144 = 20 \cdot 4 + \frac{1}{2} \cdot a \cdot 4^{2}$ Vi skal finne den $a$ -en som passer inn i likningen over. Dette er det samme som å løse en likning med hensyn på $x$ , men vi har byttet ut bokstaven $x$ med bokstaven $a$ . En god strategi for å løse likninger er å først samle alle leddene med den ukjente variabelen i på én side. Dette gjør vi her ved å subtrahere $20 \cdot 4 = 80$ på begge sider av likhetstegnet. Da får vi $\frac{1}{2} \cdot a \cdot 4^{2} = 144 - 80 .$ Vi legger sammen høyre side og får $\frac{1}{2} \cdot a \cdot 4^{2} = 64 .$ Uttrykket på venstre side er litt rotete. Siden multiplikasjonens rekkefølge er likegyldig, kan vi skrive den venstre siden i $\frac{1}{2} \cdot a \cdot 4^{2} = 64$ som $\frac{1}{2} \cdot 4^{2} \cdot a,$ som er lik $8 \cdot a$ . Dermed kan $\frac{1}{2} \cdot a \cdot 4^{2} = 64$ skrives som $8 \cdot a = 64 .$ For å få $a$ alene på venstre side er alt vi trenger å gjøre å dividere med $8$ . $\frac{8 \cdot a}{8} = \frac{64}{8} = 8 .$ Dermed har vi funnet ut at $a = 8$ .

Svar: Vi har at $a = 8$ .

Mer om:

Denne oppgaven er om

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

Lineære ligninger

Ligninger der alle de ukjente opptrer i første grad.

Eksempel: $2 x - 10 + x = x + 20$

linære likninger

For flere eksempler og forklaringer se artikkelen Lineære likninger i lynkurset Likninger.

For å øve mer, se oppgavesettet om førstegradslikninger i Treningsleieren.

Visste du at:

Hvis vi tolker likningen som etter forrige oppgave, har vi funnet ut at hvis et objekt med startshastighet 20 m/s har reist 144 meter på 4 sekunder, så må objektet ha en akselerasjon på 4 m/s $^{2}$ (hvis objektet har konstant akselerasjon).

Oppgave 9 (3 poeng) Nettkode: E-4B2A

Anders skal leie en bil hos bilfirma A eller bilfirma B. Grafene nedenfor viser hvor mye han må betale til hvert firma dersom han leier bilen én dag og kjører $x$ kilometer.

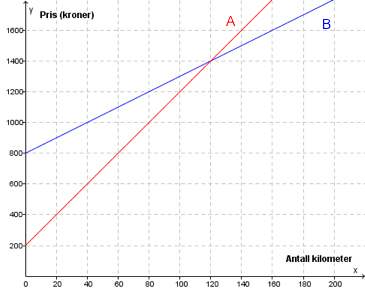
a)

Sett opp et funksjonsuttrykk for hver av de to grafene.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker:

Begge

Graf

grafene

er rette linjer (altså lineære), så funksjonsuttrykkene er på formen

a x + b

. Vi kan finne

Konstant

En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.

Eksempel: $A = π r^{2}$ , $π$ er en konstant og $r$ er en variabel.

Se Variabel

konstantledded

ved å se på

y-akse

Den loddrette aksen i et koordinatsystem.
Kalles også andreaksen.

y-aksen.

Siden grafene er lineære, er funksjonsuttrykkene deres på formen $a x + b$ . Vi tar grafen $A$ først. La oss si at funksjonen til $A$ er gitt ved $f (x) = a x + b$ , der $a$ og $b$ er konstanter. Vi må finne disse konstantene. Vi ser at $A$ krysser $y$ -aksen i $y = 200$ ; dette betyr at når $x = 0$ så er $y = f (0) = 200$ . På den andre siden vet vi allerede fra funksjonsuttrykket at $f (0) = a \cdot 0 + b$ , så vi får $a \cdot 0 + b = 200 .$ Siden $a \cdot 0 + b = b$ , er konstantleddet lik 200! Nå gjenstår det å finne $a$ , som er stigningstallet til grafen. Stigningstallet til en graf er hvor mye $y$ -verdien øker når $x$ -verdien øker med 1. En annen måte å se på det på er forholdet mellom endring i $y$ -verdi og og endring i $x$ -verdi. Siden ligningen er lineær har det ikke noe å si hvilken endring i $x$ -verdi vi velger. La oss si at vi starter med $x = 0$ og øker med 20. Hvor mye øker $y$ med da? Vi har $f (0) = 200$ og $f (20) = 400$ , så $y$ -verdien endrer seg med 200. Forholdet mellom endringene er da

$\frac{endring i y - verdi}{endring i x - verdi} = \frac{200}{20} = 10$

så stigningstallet er $a = 10$ . Dermed er funksjonsuttrykket til $A$ lik $f (x) = 10 x + 200$ .

For $B$ gjør vi det samme. Vi ser at grafen krysser $y$ -aksen i $y = 800$ , så konstantleddet til funksjonen er 800. Når vi lar $x$ øke fra 0 til 40, så øker $y$ -verdien fra 800 til 1000 – altså øker $y$ -verdien med 200. Stigningstallet er forholdet mellom disse, altså $\frac{200}{40} = 5$ . Dermed er funksjonsuttrykket til $B$ lik $g (x) = 5 x + 800$ .

Svar: For $A$ er funksjonsuttrykket $y = 10 x + 200$ , og for $B$ er funksjonsuttrykket $y = 5 x + 800$ .

Mer om:

Denne oppgaven er om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.

Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.

stigningstall

Graf

graf

For flere eksempler og forklaringer se artikkelen Rette linjer (lineære funksjoner). For mer om om funksjoner og grafer se lynkurset Funksjoner.

For å øve mer, se oppgavesettet om lineære funksjoner i Treningsleieren.

Visste du at:

Stigningstallet til grafene er det samme som hvor mye det koster å kjøre en bil i én kilometer.

b)

Hva forteller den grafiske framstillingen om de to pristilbudene?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker:

Vi ser at

Graf

grafene

krysser hverandre når

x = 120

, og det betyr at prisen er det samme når man kjører 120 kilometer. Vi kan sammenligne hvem som ligger øverst før og etter dette punktet; lavere

y

-verdier gir betyr lavere priser.

Grafene krysser hverandre når $x = 120$ . Før det ligger grafen $A$ under grafen $B$ , og det betyr at prisen er lavere hos bilfirma $A$ enn hos bilfirma $B$ hvis Anders kjører kortere enn $120$ kilometer. Når $x \geq 120$ er derimot grafen $B$ lavest, så hvis Anders skal kjøre lengre enn 120 kilometer vil det lønne seg for han å benytte seg av bilfirma $B$ .

Svar: For $x < 120$ er $A$ billigst; når $x > 120$ er $B$ billigst.

Mer om:

Denne oppgaven er om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

Graf

graf

Skjæringspunkt

Der to eller flere linjer krysser hverandre, sier vi at de har et felles skjæringspunkt. I et koordinatsystem kan skjæringspunktet leses av ved å trekke en loddrett strek ned til x-aksen og en vannrett strek bort til y-aksen.

skjæringspunkt

For flere eksempler og forklaringer se artikkelen Grafisk løsning av likninger. For mer om funksjonsdrøfting se lynkurset Funksjonsdrøfting.

For å øve mer, se oppgavesettet om skjæringspunkt i Treningsleieren.

c)

Er antall kilometer han kjører, og prisen han totalt må betale, proporsjonale størrelser? Begrunn svaret ditt.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker:

At størrelsene er

Proporsjon

Proporsjon betyr at to forhold er like.

Eksempel: a forholder seg til b som c forholder seg til d, $\frac{a}{b} = \frac{c}{d}$

proposjonale

betyr at forholdet mellom

f (x)

x

er det samme, uansett hvilken verdi man putter inn for

x

. Dette kan vi sjekke ved å sette inn noen forskjellige verdier for

x

La oss se på $A$ . Hvis antall kilometer og totalpris hadde vært proposjonale, skulle det vært slik at $\frac{f (x)}{x}$ skulle vært konstant for alle $x$ man putter inn, altså skulle $\frac{f (10)}{10} = \frac{f (20)}{20}$ og $\frac{f (20)}{20} = \frac{f (100)}{100}$ . Dette kan vi sjekke ved å sette inn verdier for $x$ ! Vi får at $\frac{f (20)}{20} = \frac{400}{20} = 20$ og $\frac{f (100)}{100} = \frac{1200}{100} = 12$ , og disse er ikke like. Derfor er ikke størrelsene proposjonale. (Det samme gjelder også for $B$ -grafen.)

Vi kan også se at størrelsene ikke er proposjonale ved at de ikke starter i origo.

Svar: Nei, størrelsene er ikke proposjonale.

Mer om:

Denne oppgaven er om

Proporsjon

Proporsjon betyr at to forhold er like.

Eksempel: a forholder seg til b som c forholder seg til d, $\frac{a}{b} = \frac{c}{d}$

forhold

For flere eksempler og forklaringer se artikkelen Proporsjonalitet.

For å øve mer, se oppgavesettet om proporsjonale funksjoner i Treningsleieren.

Visste du at:

Hvis størrelsen $x$ skal være proposjonal med størrelsen $y$ , så må $\frac{y}{x} = a$ være

Konstant

En konstant er en størrelse som ikke forandrer verdi, i motsetning til en variabel.

Eksempel: $A = π r^{2}$ , $π$ er en konstant og $r$ er en variabel.

Se Variabel

konstant

for alle samsvarende verdier av

x

y

. Hvis man plotter grafen til

y

mot

x

, så vil størrelsene være proposjonale hvis og bare hvis grafen er lineær og går gjennom origo (der

x = y = 0

)! Dette er fordi hvis

x

går mot 0, så må

y

også gå mot 0 for å hindre at forholdet deres går mot uendelig.

Oppgave 10 (2 poeng) Nettkode: E-4B2L

Du har en boks med form som et rett, firkantet prisme og en boks med form som en sylinder. De to boksene er like høye.

Grunnflaten i det rette, firkantede prismet er et rektangel med sider 7 cm og 4 cm. Radius i sylinderen er 3 cm.

Hvilken boks har størst volum?

Løs oppgaven her

Løsningsforslag

Jeg tenker:

Vi vet hvordan vi regner ut

Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm³) og kubikkmeter (m³).

volumet

til rette, firkantede

Prisme

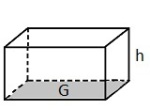
Et prisme er en tredimensjonal figure satt sammen av parallelle, kongruente mangekanter (som topp og bunnflate) og med sideflater som alle er parallellogrammer.

Har et prisme grunnflate G og høyde h, er volumet lik G · h.

prismer

Sylinder

En sylinder er en tredimensjonal figur. En vanlig sylinder er satt sammen av to identiske sirkler og et rektangel.

sylindere

, så vi regner ut volumet til begge boksene og sammenligner.

For å sammenligne volumet til de to boksene, må vi regne dem ut. Formelen for volumet til slike bokser er gitt ved $V = G \cdot h,$ der for $G$ er arealet til grunnflaten, og $h$ er høyden til boksen. La oss starte med det firkantede prismet. Grunnflaten til boksen er et rektangel med sider 7 cm og 4 cm, så arealet til grunnflaten er 7 cm $\cdot$ 4 cm $= 28$ cm $^{2}$ . Dermed blir volumet til det firkantede prismet lik $28 {cm}^{2} \cdot h$ , der $h$ er høyden. Vi vet ikke hva høyden er, så vi lar dette uttrykket stå som det er inntil videre.

Grunnflaten i sylinderen er en sirkel med radius 3 cm. Formelen for arealet til en sirkel med radius $r$ er $A = π r^{2}$ , så arealet til grunnflaten er $π \cdot (3 cm)^{2} = 9 π {cm}^{2}$ . Vi vet at $π \approx 3, 14$ , så volumet blir cirka $V = 9 π {cm}^{2} \cdot h \approx 9 \cdot 3, 14 {cm}^{2} \cdot h = 28, 26 {cm}^{2} \cdot h,$ der $h$ er høyden.

Vi vet fremdeles ikke hvor høye boksene er, men uansett hvor høy eller lav boksene er, vil $28, 26 {cm}^{2} \cdot h$ være større enn $28 {cm}^{2} \cdot h$ – derfor har den sylinderformede boksen størst volum.

Svar: Den sylinderformede boksen har størst volum.

Mer om:

Denne oppgaven er om

Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm³) og kubikkmeter (m³).

volum

Prisme

prisme

Sylinder

En sylinder er en tredimensjonal figur. En vanlig sylinder er satt sammen av to identiske sirkler og et rektangel.

sylinder

For flere eksempler og forklaringer se artiklene En sylinder og Et rett prisme i lynkurset Geometri - areal og volum.

For å øve mer, se oppgavesettet om volum i Treningsleieren.

DEL 2 Med hjelpemidler

Oppgave 1 (3 poeng) Nettkode: E-4B2O

Da forslaget til statsbudsjett for 2015 ble lagt fram, var dette et av oppslagene på nettsidene til avisen Dagens Næringsliv:

a)

Hva kan du si om størrelsen på de direkte overføringene til FN-organisasjoner før dette?

Løs oppgaven her

Løsningsforslag a)

Jeg tenker:

Hvis vi antar at kuttet er på cirka $20 %$ , så er de totale overføringene før kuttet cirka 5 ganger så stor.

Teksten sier at kuttet i de direkte overføringene på 906 millioner er cirka $20 %$ av totalbeløpet. Hvis vi lar $x$ være det totale beløpet før kuttet i millioner, så kan vi skrive dette mer matematisk som $20 % \cdot x \approx 906 .$ Vi går “veien om 1”, og gjør om $20 %$ til $0, 2$ . Da får vi at $0, 2 \cdot x \approx 906 .$ Vi vil finne et tall $x$ som passer inn i ligningen over, og derfor vil vi ikke at det skal stå noe foran $x$ på venstre side. Derfor multipliserer vi med 5 på begge sider. $\begin{matrix} 5 \cdot 0, 2 \cdot x \approx 5 \cdot 906, \\ x \approx 4530 . \end{matrix}$

Altså kan vi konkludere med at regjeringen hadde direkte overføringer på cirka $4, 53$ milliarder kroner til FN-organisasjoner før kuttet.

Svar: Størrelsen på de direkte overføringene lå på cirka $4, 53$ milliarder kroner før kuttet.

Mer om:

Denne oppgaven er om

Prosent

Prosent betyr hundredel og skrives %.

Eksempel: Hvor mange prosent er 1 av 4? $\frac{1}{4} = \frac{1 \cdot 25}{4 \cdot 25} = \frac{25}{100} = 25 %$ .

prosent

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

For flere eksempler og forklaringer se artikklen Regneregler i lynkurset Prosent og artikkelen Lineære likninger.

For å øve mer, se oppgavesettet om prosentregning i Treningsleieren.

Visste du at:

Teksten sier egentlig bare at kuttet i overføringene lå på over $20 %$ , så det eneste vi faktisk kan konkludere med er at de totale overføringene lå på under $4, 53$ milliarder.

b)

Med hvor mange prosent ville regjeringen redusere støtten til FNs barneorganisasjon UNICEF?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker:

Teksten sier at beløpet ble halvert, så svaret er rundt $50 %$ .

I oppgaveteksten står det at støtten til UNICEF er bortimot halvvert. Å halvvere noe er det samme som å multiplisere det med $\frac{1}{2} = 50 %$ , så svaret vi leter etter skal være cirka $50 %$ . Dette kan være en godt sjekk for å finne ut om det nøyaktige svaret man kommer fram til er riktig.

Det står at støtten til UNICEF ble redusert fra 1 milliard til 520 millioner kroner. Husk at 1 milliard er det samme som 1000 millioner. Dermed er støtten redusert med $1000 - 520 = 480$ millioner kroner. Oppgaven går ut på å finne ut hvor mange prosent av 1 milliard dette er. Vi kan gjøre det på flere måter. Den generelle fremgangsmetoden for å finne ut hvor stor prosentandel et tall $a$ er av et annet tall $b$ , er å se på forholdet mellom de to: tallet $a$ er $\frac{a}{b} \cdot 100 %$ av $b$ . Skal vi for eksempel finne ut hvor mange prosent 1 er av 4, får vi $\frac{1}{4} \cdot 100 % = 25 %$ , altså en fjerdedel. I vårt tilfelle får vi at 480 millioner er $\frac{480}{1000} \cdot 100 % = 4, 8 \cdot 100 % = 48 %$ av 1 milliard. Dette er cirka $50 %$ , akkurat som vi trodde.

Denne måten å gjøre det på vil alltid fungere, men i denne oppgaven kan det være enklere å se at $480$ av $1000$ er det samme som å ta $48$ av $100$ ; siden “prosent” betyr “per hundre” ser vi at svaret blir $48 %$ . På denne måten kan man spare tid på eksamen.

Svar: $48 %$ .

Mer om:

Denne oppgaen er om

Prosent

Prosent betyr hundredel og skrives %.

Eksempel: Hvor mange prosent er 1 av 4? $\frac{1}{4} = \frac{1 \cdot 25}{4 \cdot 25} = \frac{25}{100} = 25 %$ .

prosent

Proporsjon

Proporsjon betyr at to forhold er like.

Eksempel: a forholder seg til b som c forholder seg til d, $\frac{a}{b} = \frac{c}{d}$

forhold

Hvis du vil vite mer om prosent og prosentregning, se artikkelen Hva er prosent? i lynkurset Prosent.

For å øve mer, se oppgavesettet om prosentregning i Treningsleieren.

Oppgave 2 (4 poeng) Nettkode: E-4B2R

Ved en skole er det 437 elever. 164 av elevene drikker melk hver dag. 316 av elevene drikker juice hver dag. 67 av elevene drikker verken melk eller juice hver dag.

a)

Lag et venndiagram eller en krysstabell som beskriver situasjonen ovenfor.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker:

Vi skal sette opp informasjonen vi har fått i oppgaveteksten på en systematisk måte. Vi lager en

Krysstabell

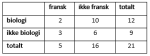
En krysstabell er en måte å framstille data på. Når tabellen er satt opp, er det enklere å finne den ønskede sannsynligheten.

krysstabell

og etter det et Venn-diagram.

Vi setter opp en krysstabell. Vi har to muligheter for melk: Enten drikker man melk, eller så gjør man det ikke. Det samme gjelder for juice. Da kan vi sette opp det følgende skjemaet:

	Melk	Ikke melk	Totalt
Juice
Ikke juice
Totalt

Oppgaveteksten sier at 164 av elevene drikker melk hver dag. Siden det er 437 elever totalt, er det $437 - 164 = 273$ elever som ikke drikker melk hver dag. Dette kan vi fylle inn i skjemaet. Vi går ned til rekken som sier “Totalt” på venstre side. I kolonnen “Melk” skriver vi 164, og i kolonnen “Ikke melk” skriver vi 273. I kolonnen “Totalt” kan vi skrive $173 + 164 = 437$ , siden det totalt er $437$ som enten drikker melk eller ikke drikker melk.

	Melk	Ikke melk	Totalt
Juice
Ikke juice
Totalt	$164$	$273$	$437$

Det samme gjør vi for “Totalt”-kolonnen loddrett nedover. I første rute skriver vi 316, siden det er så mange elever som drikker juice. I “Ikke juice”-raden skriver vi $437 - 316 = 121$ . Vi har fått én opplysning til, nemlig at det er 67 elever som verken drikker melk eller juice hver dag. Dermed kan vi føre inn 67 i kolonnen “Ikke melk” der den krysser med “Ikke juice”.

	Melk	Ikke melk	Totalt
Juice			$316$
Ikke juice		$67$	$121$
Totalt	$164$	$273$	$437$

Nå er det tre ruter igjen som vi må fylle inn. La oss først ta rekken der det står “Ikke juice” – vi skal fylle inn den første ruten, og i de neste rutene står det henholdsvis 67 og 121. Ved å lese hva som står øverst i kolonnen med 121 (det står “Totalt”), vet vi at hvis vi summerer det som skal stå i den første ruten med det som står i den andre ruten, skal vi få 121. La $x$ betegne det som skal stå i første rute, som vist under.

	Melk	Ikke melk	Totalt
Juice			$316$
Ikke juice	$x$	$67$	$121$
Totalt	$164$	$273$	$437$

Vi skal altså finne en verdi for $x$ sånn at $x + 67 = 121 .$ Vi løser denne ligningen ved å trekke fra 67 på begge sider, og får $x = 121 - 67 .$ Vi ser at $121 - 67 = 54$ , og da blir $x = 54,$ så det skal stå 54 i den første ruten.

	Melk	Ikke melk	Totalt
Juice			$316$
Ikke juice	$54$	$67$	$121$
Totalt	$164$	$273$	$437$

Nå kan vi gjøre det samme for kolonnene “Melk” og “Ikke melk”. Hvis $y$ er tallet som skal stå der kolonnen “Melk” krysser raden “Juice”, og “z” er det som skal stå der “Ikke melk” krysser “Juice”, så får vi $\begin{matrix} y + 54 & = 164 og \\ z + 67 & = 273 . \end{matrix}$ Vi flytter tallene slik at de ukjente står alene på venstre side, og får $\begin{matrix} y & = 164 - 54 og \\ z & = 273 - 67 . \end{matrix}$ Vi trekker sammen det som står på de høyre sidene, og får $\begin{matrix} y & = 110 \\ z & = 206 . \end{matrix}$ Til slutt fyller vi dette inn i tabellen vår.

	Melk	Ikke melk	Totalt
Juice	$110$	$206$	$316$
Ikke juice	$54$	$67$	$121$
Totalt	$164$	$273$	$437$

Vi kunne også valgt å lage et venndiagram. Utregningene hadde vært de samme, og resultatet ville vært noe som følgende:

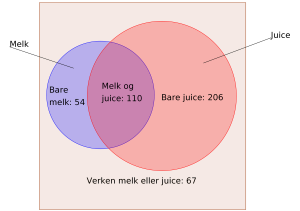
Svar: Enten

	Melk	Ikke melk	Totalt
Juice	$110$	$206$	$316$
Ikke juice	$54$	$67$	$121$
Totalt	$164$	$273$	$437$

eller

Mer om:

Denne oppgaven er om

Krysstabell

En krysstabell er en måte å framstille data på. Når tabellen er satt opp, er det enklere å finne den ønskede sannsynligheten.

krysstabell

og Venn-diagram.

For flere eksempler og forklaringer se artikkelen Venn-diagram og mengdelære.

b)

Bestem sannsynligheten for at en tilfeldig valgt elev ikke drikker melk hver dag.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker:

Vi bruker

Krysstabell

En krysstabell er en måte å framstille data på. Når tabellen er satt opp, er det enklere å finne den ønskede sannsynligheten.

krysstabellen

vår og slår opp hvor mange som ikke drikker melk. Vi husker at vi har forholdet

$sannsynlighet = \frac{gunstige}{mulige} .$

Det er totalt 437 elever på skolen, og i følge krysstabellen vår er det 273 elever som ikke drikker melk hver dag. Hvis vi velger en tilfeldig elev, er da $\frac{273}{437} \cdot 100 %$ sannsynligheten for at denne eleven ikke drikker melk hver dag. Dette får vi fra at likningen $sannsynlighet = \frac{gunstige}{mulige}$ . Taster vi dette inn på kalkulatoren, får vi

$\frac{273}{437} \cdot 100 % = 62, 471 . . . % \approx 62, 47 %$

Svar: Sannsynligheten er cirka $62, 47 %$ for at en tilfeldig valgt elev ikke drikker melk hver dag.

Mer om:

Denne oppgaven er om

Krysstabell

En krysstabell er en måte å framstille data på. Når tabellen er satt opp, er det enklere å finne den ønskede sannsynligheten.

krysstabell

Sannsynlighet

sannsynlighet

For flere eksempler og forklaringer se artikkelen Hvordan finner vi uniform sannsynlighet? og for mer om prosent og prosentregning, se lynkurset Prosent.

For å øve mer, se oppgavesettet om sannsynlighetsregning i Treningsleieren.

Visste du at:

Legg merke til at sannsynligheten for at en tilfeldig valgt elev drikker ikke drikker melk, er den samme som prosentandelen som ikke drikker melk!

c)

Bestem sannsynligheten for at en tilfeldig valgt elev som drikker melk hver dag, også drikker juice hver dag.

Løs oppgaven her

Løsningsforslag c)

Jeg tenker:

Vi kan igjen bruke

Krysstabell

En krysstabell er en måte å framstille data på. Når tabellen er satt opp, er det enklere å finne den ønskede sannsynligheten.

krysstabellen

vår.

Vi vet at det er totalt 164 av elevene som drikker melk hver dag, og vi skal regne ut sannsynligheten for at en tilfeldig valgt elev blant disse også drikker juice hver dag. I krysstabellen vår går vi til “Melk”-kolonnen, og under “Juice”-raden står det 110. Det betyr at det er 110 som drikker juice av de 164 som også drikker juice. Dermed blir sannsynligheten for at en tilfeldig valgt juicedrikker også drikker melk lik

$\frac{110}{164} \cdot 100 % = 67, 073 . . . % \approx 67, 07 %$

Svar: Sannsynligheten for at en tilfeldig valgt melkedrikker også drikker juice er cirka $67, 07 %$ .

Mer om:

Denne oppgaven er om

Sannsynlighet

sannsynlighet

For flere eksempler og forklaringer se lynkurset Sannsynlighet (del II). For flere eksempler og forklaringer om prosentregning se lynkurset Prosent.

For å øve mer, se oppgavesettet om sannsynlighetsregning i Treningsleieren.

Oppgave 3 (2 poeng) Nettkode: E-4B2V

Prisen på en vare er endret flere ganger. Først ble prisen satt opp med 20 %. Senere ble den satt opp med 10 % til. En stund etter ble prisen så satt ned med 30 %. Nå koster varen 3 234 kroner.

Hva kostet varen før prisen endret seg første gang?

Løs oppgaven her

Løsningsforslag

Jeg tenker:

Vi ser at prisen blir satt opp totalt $30 %$ og deretter ned $30 %$ , så det kan være fristende å si at prisen ikke har forandret seg. Dette stemmer ikke! Det er fordi $30 %$ av en lavere pris ikke er det samme som $30 %$ av en høyere pris. For eksempel er $10 %$ av 100 lik $10$ , mens $10 %$ av 110 er 11. Derfor må vi finne på noe annet. Vi lar den opprinnelige prisen være ukjent, så kommer vi fram til en ligning ved å følge teksten.

La den opprinnelige vareprisen være $x$ kroner. Først ble prisen satt opp $20 %$ . Vi vet at $20 %$ av $x$ er $20 % \cdot x$ , og den nye prisen er dette tallet addert med $x$ . Det betyr at den nye prisen har blitt $x + 20 % \cdot x$ . Husk at $20 %$ er det samme som $\frac{1}{5}$ , så vi kan skrive prisen som $x + \frac{1}{5} x = \frac{6}{5} x = 1, 2 \cdot x .$ Dette kan vi også se ved at $vekstfaktor = 1 + prosentfaktor,$ og prosentfaktoren til $20 %$ er $0, 2$ .

Senere ble prisen satt opp $10 %$ til. Vi merker oss at varen ble satt opp $10 %$ i forhold til prisen etter den første prisendringen. Den nye vekstfaktoren blir $1, 1$ , og den nye prisen blir $1, 1 \cdot (1, 2 \cdot x) = 1, 32 \cdot x .$ Her merker vi oss at $1, 32 = 132 %$ , så den nye prisen er $132 %$ av den originale. Det betyr at den nye prisen er $32 %$ høyere enn den originale prisen, og ikke $30 %$ , som man kanskje kunne trodd. Til slutt ble varen satt ned med $30 %$ , så da må vi trekke fra $30 %$ av prisen ovenfor. Prosentfaktoren til $30 %$ er $0, 3$ , og vekstfaktoren blir $1 - 0, 3 = 0, 7$ . Legg merke til at vi subtraherer prosentfaktoren, siden prisen reduseres. Sluttprisen blir dermed $0, 7 \cdot 1, 32 \cdot x$ som igjen blir $0, 924 \cdot x$ . Men vi vet allerede at sluttprisen er lik 3234 kroner, så vi før følgende ligning: $0, 924 \cdot x = 3234 .$ Vi vil løse denne ligningen for $x$ , så vi dividerer med $0, 924$ på begge sider og får $x = \frac{3234}{0, 924} = 3500 .$ Altså kostet varen i utgangspunktet 3500 kroner. Det betyr at varen har blitt billigere!

Svar: Varen kostet 3500 kroner.

Mer om:

Denne oppgaven er om prosent,

Prosentfaktor

En prosentfaktor er et prosenttall skrevet om til et desimaltall.

Eksempel: 32 % blir skrevet som 0,32 når det skal skrives som en prosentfaktor.

prosentfaktor

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likning

Hvis du vil vite mer om prosent og prosentregning, se artikkelen Prosent av hva da? i lynkurset Prosent. For flere forklaringer og eksempler om likninger se artikkelen Lineære likninger.

For å øve mer, se oppgavesettet om prosentregning i Treningsleieren.

Visste du at:

Som vi ser i denne oppgaven, er det ikke slik at et tall blir uendret hvis vi først legger til $10 %$ av tallet og deretter subtraherer $10 %$ fra resultatet. Stemmer det med hvordan vi forstår prosentregning?

Oppgave 4 (4 poeng) Nettkode: E-4B2Y

Ovenfor ser du en boks «Stabbur-Makrell». Bunnen av boksen er tilnærmet lik et rektangel og to halvsirkler og har form som vist på figuren til høyre. Rektangelet har lengde 8,2 cm og bredde 6,6 cm.

Anta at sideflaten står vinkelrett på topp og bunn, og at boksen er 2,1 cm høy.

a)

Bestem volumet av boksen.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker:

Vi må regne ut

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

arealet

Rektangel

Et rektangel er en firkant der sidene er parvis like lange og alle vinklene er 90°.

Areal: $A = a b$

Omkrets: $O = 2 a + 2 b$

rektangelet

og de to halvsirklene.

Volumet $V$ til en figur som i oppgaven er gitt ved

$V = g \cdot h, (7)$

hvor $g$ er arealet til grunnflaten og $h$ er høyden til figuren. For å finne volumet til boksen er det derfor lurt å starte med å finne arealet til bunnen. Bunnen består av et rektangel og to halvsirkler. Arealet til rektangelet er lengden multiplisert med bredden, altså $6, 6 cm \cdot 8, 2 cm = 54, 12 {cm}^{2} .$ Så må vi regne ut arealet av halvsirklene. Vi kan regne ut arealet av hver halvsirkel for seg, men hvis vi setter dem sammen får vi en hel sirkel, så vi trenger bare å regne ut arealet til denne. Fra tegningen i oppgaven ser vi at hver halvsirkel er $8, 2 cm$ høy, eller med andre ord at diameteren i hver halvsirkel er $8, 2 cm$ . Setter vi halvsirklene sammen får vi altså en sirkel med radius $\frac{8, 2 cm}{2} = 4, 1 cm$ . Formelen for arealet til en sirkel med radius $r$ er gitt ved $π \cdot r^{2}$ , så arealet til sirkelen vår er $π \cdot (4, 1 cm)^{2} \approx 52, 81 {cm}^{2}$ .

Hvis vi ville regne ut hver halvsirkel for seg, ville vi fått at hver halvsirkel har areal $\frac{1}{2} \cdot π \cdot r^{2} = \frac{1}{2} \cdot π \cdot (4, 1 cm)^{2}$ . Vi har to halvsirkler, hvis vi multipliserer dette stykket med to, får vi det samme svaret som ovenfor.

Nå har vi funnet arealet til alle figurene i bunnen av boksen, og det totale arealet av bunnen til boksen er disse tallene addert sammen. Med andre ord er arealet til grunnflaten lik cirka $54, 12 {cm}^{2} + 52, 81 {cm}^{2} = 106, 93 {cm}^{2} .$ Høyden til boksen er $2, 1 cm$ , så volumet $V$ blir, ut i fra (7) lik $V = 106, 93 {cm}^{2} \cdot 2, 1 cm \approx 224, 55 {cm}^{3} .$

Svar: Volumet er cirka $224, 55 {cm}^{3}$ .

Mer om:

Denne oppgaven er om

Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm³) og kubikkmeter (m³).

volum

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

Rektangel

Et rektangel er en firkant der sidene er parvis like lange og alle vinklene er 90°.

Areal: $A = a b$

Omkrets: $O = 2 a + 2 b$

rektangel

Sirkel

Sirkel brukes i to betydninger:

1) Selve sirkellinjen som er den krumme linjen som går gjennom punktene som har samme avstand fra et fast punkt, nemlig sentrum i sirkelen. Dette er det samme som sirkelen sin omkrets.

2) Flaten som sirkellinjen begrenser.

Areal: $A = π r^{2}$
Omkrets: $O = 2 π r$

sirkel

For flere eksempler og forklaringer se artikklen Et rektangel i lynkurset Geometri - areal og volum og Alt om sirkel i lynkurset Geometri - vinkler og figurer. .

For å øve mer, se oppgavesettet om volum i Treningsleieren.

b)

Bestem overflaten av boksen.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker:

Overflatearealet til boksen er

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

arealet

til bunnflaten, arealet til toppen og sidearealet addert sammen. Vi kan bruke arealet vi fant i forrige oppgave. Vi kan også se at sideflaten blir til et

Rektangel

Et rektangel er en firkant der sidene er parvis like lange og alle vinklene er 90°.

Areal: $A = a b$

Omkrets: $O = 2 a + 2 b$

rektangel

når den brettes ut.

Vi antar at arealet til toppen er det samme som arealet til bunnen. Arealet til bunnen vet vi fra forrige oppgave er cirka $106, 93 {cm}^{2}$ , så det gjenstår bare å finne arealet til sidene av boksen.

Vi vil finne arealet til sidekantene av boksen. Vi ser at hvis vi “bretter ut” sidekanten, så får vi et rektangel, og arealet av et rektangel er grunnlinjen multiplisert med høyden. Grunnlinjen tilsvarer omkretsen rundt bunnen av boksen, og høyden i rektangelet tilsvarer høyden i boksen. Derfor kan vi finne arealet til sidene ved å finne omkretsen til bunnflaten, og multiplisere opp med høyden. Rektangelet i bunnen av boksen bidrar med to sider til omkretsen. Begge disse sidene er $6, 6 cm$ lange. Bidraget fra de to sirkelhalvdelene regner vi ut ved å regne ut omkretsen til sirkelen med radius $8, 2 cm$ – vi kan nemlig fremdeles sette sammen de to sirkelhalvdelene til en hel sirkel i stedet for å regne ut arealbidraget til hver halvdel. Formelen for omkretsen av en sirkel med radius $r$ er $2 \cdot π \cdot r$ , så bidraget fra sirkelhalvdelene til omkretsen er $2 \cdot π \cdot 4, 1 cm \approx 25, 76 cm$ .

Nå kan vi sette sammen det vi har funnet ut. Omkretsen til bunnflaten av boksen er bidraget fra sirkelhalvdelene pluss de to bidragene fra sidene til rektangelet, og totalt blir omkretsen blir cirka $25, 76 cm + 2 \cdot 6, 6 cm = 38, 96 cm .$ For å finne arealet av sidekanten må vi multiplisere med høyden av boksen, og det endelige svaret blir $38, 96 cm \cdot 2, 1 cm \approx 81, 82 {cm}^{2} .$

Overflatearealet til hele boksen blir arealet til toppen, til bunnen og til siden summert opp. Altså blir det endelige arealet lik cirka $2 \cdot 106, 93 {cm}^{2} + 81, 82 {cm}^{2} = 295, 68 {cm}^{2} .$

Svar: Overflatearealet til boksen er cirka $295, 68 {cm}^{2}$ .

Mer om:

Denne oppgaven er om

Overflate

Med overflate av en tredimensjonal figur, for eksempel et prisme eller en sylinder, menes summen av arealene til alle flatene som den tredimensjonale figuren er satt sammen av.

overflateareal

Areal

Areal kalles også for flatemål eller flateinnhold og angir hvor stor en flate er.
Noen måleenheter for areal er m², dm² og cm².

areal

Rektangel

Et rektangel er en firkant der sidene er parvis like lange og alle vinklene er 90°.

Areal: $A = a b$

Omkrets: $O = 2 a + 2 b$

rektangel

For flere forklaringer og eksempler se artikkelen Et rektangel i lynkurset Geometri - areal og volum.

For å øve mer, se oppgavesettet om overflateareal i Treningsleieren.

Oppgave 5 (8 poeng) Nettkode: E-4B31

En bedrift bruker i en periode vann fra et basseng i produksjonen av et nytt produkt.

Funksjonen $f$ gitt ved

$f (x) = 0, 0013 x^{3} - 0, 59 x^{2} + 61 x + 2000, 0 \leq x \leq 300$

viser vannstanden $f (x)$ millimeter i bassenget x dager etter at fabrikken startet produksjonen av produktet.

a)

Bruk graftegner til å tegne grafen til $f$ .

Løs oppgaven her

Løsningsforslag a)

Jeg tenker:

Vannstanden er avstanden fra bunnen i bassenget til vannoverflaten. Vi bruker

GeoGebra

GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.

GeoGebra

til å tegne

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjonen

til vannstanden.

I Skriv inn-boksen skriver vi følgende:

Funksjon[0.0013x^3 - 0.59x^2 + 61x + 2000, 0, 300]

Dette betyr at vi plotter funksjonen $f$ oppgitt i oppgaven for $0 \leq x \leq 300$ . Deretter drar vi aksene med shift-tasten og musepekeren slik at $x$ -aksen viser intervallet fra 0 til 300, og vi drar $y$ -aksen slik at hele grafen vises. Husk at konstantleddet er 2000, så funksjonen tar ganske høye verdier. Vi må huske å sette navn på aksene. Dette gjør vi ved å høyreklikke i grafikkfeltet, velge “Innstillinger” og skrive inn aksenavn under xAkse og yAkse.

Svar:

Mer om:

Denne oppgaven er om

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

Graf

graf

GeoGebra

GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.

GeoGebra

For flere eksempler og forklaringer om funksjoner og grafer se lynkurset Funksjoner. Lynkurset om GeoGebra er under utarbeidelse og kommer snart.

For å øve mer, se oppgavesettet om grafisk fremstilling i Treningsleieren.

b)

Bestem forskjellen mellom høyeste og laveste vannstand i bassenget i denne perioden.

Løs oppgaven her

Løsningsforslag b)

Jeg tenker:

Vi skal finne forskjellen mellom det nederste punktet på grafen og det høyeste punktet på grafen, med andre ord forskjellen mellom

Toppunkt

Et toppunkt for en funksjon er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er større enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

toppunktet

Bunnpunkt

Et bunnpunkt for en funksjon $f (x)$ er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er mindre enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

bunnpunktet

Vi bruker

GeoGebra

GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.

GeoGebra

. Vi må finne ekstremalverdiene til funksjonen. Disse punktene kalles ekstremalpunkter, og med kommandoen

Ekstremalpunkt[ 0.0013x^3 - 0.59x^2 + 61x + 2000 ]

finner vi ekstremalpunktene til funksjonen. Vi får som resultat at toppunktet er $(66.16, 3829.71)$ , og at bunnpunktet er $(236.4, 622.84)$ . Grafen viser at disse punktene på grafen har henholdsvis størst og minst $y$ -koordinat. De viser dermed høyeste og laveste vannstand. Vi er bedt om å finne forskjellen i $y$ -verdi mellom disse punktene, og vi får $3829, 71 - 622, 84 = 3206, 87 .$ Dette betyr at forskjellen mellom den høyeste og laveste vannstanden var $3206, 87$ millimeter, eller cirka $3, 21$ m.

Svar: $3206, 87$ mm, eller cirka $3, 21$ m.

Mer om:

Denne oppgaen er om

Ekstremalpunkt

Vi sier at et punkt $x = a$ er et ekstremalpunkt for en funksjon $f (x)$ hvis det enten er et toppunkt eller bunnpunkt for funksjonen.

ekstremalpunkt

Toppunkt

Et toppunkt for en funksjon er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er større enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

toppunkt

Bunnpunkt

Et bunnpunkt for en funksjon $f (x)$ er et punkt $(a, f (a))$ der funksjonsverdien $f (a)$ er mindre enn $f (x)$ i alle nabopunktene, altså alle punktene i et intervall rundt $a$ .

bunnpunkt

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

Graf

graf

GeoGebra

GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.

GeoGebra

For flere eksempler og forklaringer se artikkelen Topp- og bunnpunkter i lynkurset Funksjonsdrøfting. Lynkurset om GeoGebra er under utarbeidelse og kommer snart.

For å øve mer, se oppgavesettet om ekstremalpunkter i Treningsleieren.

c)

Bruk graftegner til å løse likningen $f (x) = 3000$

Hva forteller løsningene om vannstanden i bassenget?

Løs oppgaven her

Løsningsforslag c)

Jeg tenker:

Vi kan tegne en linje og finne

Skjæringspunkt

skjæringspunktet

grafisk.

Vi bruker GeoGebra. Får å løse ligningen $f (x) = 3000$ , kan vi tegne linjen $y = 3000$ og finne ut hvor linjen og $f$ krysser hverandre. For å tegne linjen i GeoGebra skriver vi

Funksjon[3000, 0, 300]

inn i Skriv inn-boksen. Resultatet blir dette.

Vi ser at linjen krysser grafen til $f$ to steder. For å finne nøyaktig ut hvor disse punktene er, bruker vi kommandoen

Skjæring[ <Funksjon>, <Funksjon>, 
<Startverdi for x>, <Sluttverdi for x> ]

Vi kunne også ha funnet skjæringspunktene ved å holde musepekeren slik at begge grafene blir markerte, og lage et punkt der. Vi fyller inn funksjonene våre, og vi lar $x$ gå mellom 0 og 300:

Skjæring[ f, g, 0, 300 ]

Vi får punktene $(20.14, 3000)$ og $(122.84, 3000)$ . Det betyr at $f (20, 14) = 3000$ , og at $f (122, 84) = 3000$ , så $x_{1} = 20, 14$ og $x_{2} = 122, 84$ er løsningene til likningen $f (x) = 3000$ . Løsningene sier oss at på dag 20 og dag 122, så er vannstanden lik 3000 millimeter, eller 3 meter.

Svar: Løsningene er $x_{1} = 20, 14$ og $x_{2} = 122, 84$ ; det vil si at på dag 20 og dag 122 er vannstanden lik 3000 millimeter.

Mer om:

Denne oppgaven er om

Skjæringspunkt

skjæringspunkt

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

Graf

graf

GeoGebra

GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.

GeoGebra

For flere forklaringer og eksempler se artikkelen Grafisk løsning av likninger og for mer om funksjoner se lynkurset Funksjonsdrøfting.

d)

Bestem stigningstallet for den rette linjen som går gjennom punktene $(90, f (90)) og (210, f (210))$ . Hva forteller dette stigningstallet om vannstanden i bassenget?

Løs oppgaven her

Løsningsforslag d)

Jeg tenker:

Vi kan regne ut

Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.

Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.

stigningstallet

ved å se på forholdet mellom endring i

y

-verdi og endring i

x

-verdi. Vi kan også bruke digitalt verktøy.

Vi kan løse dette både ved hjelp av regning og ved hjelp av digitalt verktøy. Vi starter med den første metoden.

Den rette linjen som går gjennom punktene $(90, f (90))$ og $(210, f (210))$ er en lineær funksjon. Stigningstallet til lineære funksjoner kan vi finne ved å se på forholdet mellom endring i $y$ -verdi med en tilsvarende endring i $x$ -verdi. For eksempel, hvis vi ser på funksjonen $f (x) = 2 x + 1$ , så kan vi finne stigningstallet ved å se på forholdet mellom endringen i $y$ -verdi og i $x$ -verdi når $x$ endrer seg fra 0 til 1. Stigningstallet blir:

$\frac{endring i y}{endring i x} = \frac{f (1) - f (0)}{1 - 0} = \frac{(2 \cdot 1 + 1) - (2 \cdot 0 + 1)}{1} = \frac{2}{1} = 2$

Stigningstallet er altså 2, og det samsvarer med at det står 2 foran $x$ i funksjonsuttrykket. I oppgaven vår kan vi regne ut stigningstallet til den rette linjen på samme måte, fordi vi kan regne ut endringen fra $f (90)$ til $f (210)$ og dele på endringen fra 90 til 210. Først finner vi $f (90)$ og $f (210)$ ved å sette inn i funksjonsuttrykket. $f (90) = 0, 0013 \cdot 90^{3} - 0, 59 \cdot 90^{2} + 61 \cdot 90 + 2000 = 3658, 7$

$f (210) =$

$0, 0013 \cdot 210^{3} - 0, 59 \cdot 210^{2} + 61 \cdot 210 + 2000 = 830, 3$

Nå kan vi regne ut stigningstallet.

$\begin{matrix} stigningstallet & = \frac{f (210) - f (90)}{210 - 90} \\ = \frac{830, 3 - 3658, 7}{120} = - 23, 57 . \end{matrix}$

Alternativ løsning

Som nevnt kan vi også løse problemet grafisk. Vi bruker GeoGebra. Vi vil finne stigningstallet til linjen som går gjennom $(90, f (90))$ og $(210, f (210))$ , og vi kan finne disse to punktene ved å skrive det inn i Skriv inn-feltet. Vi finner linjen som går mellom de to punktene ved å trykke på linjebildet i menyen, og deretter velge de to punktene. I algebrafeltet står det nå

a: 2828.4x + 120y = 693600

Det betyr at likningen til linjen vår er $2828, 4 x + 120 y = 693600 .$ Dette er ikke på formen vi er vant med; vi vil helst at $y$ skal stå alene på venstre side. Dette kan vi gjøre ved å høyreklikke på linjen i Geogebra, og trykke på “ $y = a x + b$ ”. Vi kan også gjøre det ved regning: Vi subtraherer $2828, 4 x$ fra hver side, og får $120 y = 693600 - 2828, 4 x .$ Vi vil ikke at noe tall skal stå foran $y$ , så vi dividerer med $120$ på hver side, og får $y = \frac{693600 - 2828, 4 x}{120} = 5780 - 23, 57 x .$ Nå har vi fått ligningen til linjen på den formen vi liker. Stigningstallet er nå det tallet som står foran $x$ , altså $- 23, 57$ .

Stigningstallet er negativt, og dette betyr at vanstanden totalt sett har sunket fra dag 90 til dag 210. Husk at stigningstallet til en graf kan tolkes som hvor mye $y$ -verdien endrer seg når $x$ -verdien endrer seg med 1, så vi kan faktisk konkludere med at vannstanden har sunket i snitt $23, 57$ millimeter hver dag i denne perioden.

Svar: Stigningstallet er $- 23, 57$ , så vannstanden har sunket i snitt $23, 57$ millimeter hver dag i perioden fra dag 90 til dag 210.

Mer om:

Denne oppgaven er om

Stigningstall

Stigningstallet forteller hvor mye grafen stiger eller synker når vi øker med en enhet på x-aksen.

Eksempel: Når vi øker enheten på x-aksen med 1, a1 = 1, fører det til at enheten på y-aksen: a2 = 4 - 2 = 2, øker med 2. Dermed er stigningstallet = 2/1 = 2.

stigningstall

Funksjon

En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).

Eksempel: For funksjonen $f (x) = 2 x + 1$ , vil $x = 1$ alltid gi $f (x) = 3$

funksjon

GeoGebra

GeoGebra er et gratis dynamisk matematikkprogram til skolebruk.

GeoGebra

Hvis du vil vite mer om lineære funksjoner, se artikkelen Rette linjer (lineære funksjoner).

For å øve mer, se oppgavesettet om lineære funksjoner i Treningsleieren.

Visste du at:

Vi kan også regne ut stigningstallet uten grafiske hjelpemidler. Den rette linjen som går gjennom punktene $(90, f (90))$ og $(210, f (210))$ er en lineær funksjon. Stigningstallet til lineære funksjoner kan vi finne ved å se på forholdet mellom endring i $y$ -verdi med en tilsvarende endring i $x$ -verdi. For eksempel, hvis vi ser på funksjonen $f (x) = 2 x + 1$ , så kan vi finne stigningstallet ved å se på forholdet mellom endringen i $y$ -verdi og i $x$ -verdi når $x$ endrer seg fra 0 til 1. Stigningstallet blir:

$\frac{endring i y}{endring i x} = \frac{f (1) - f (0)}{1 - 0} = \frac{(2 \cdot 1 + 1) - (2 \cdot 0 + 1)}{1} = \frac{2}{1} = 2$

$f (90) =$

$0, 0013 \cdot 90^{3} - 0, 59 \cdot 90^{2} + 61 \cdot 90 + 2000 =$

$3658, 7$

$f (210) =$

$0, 0013 \cdot 210^{3} - 0, 59 \cdot 210^{2} + 61 \cdot 210 + 2000 =$

$830, 3$

Nå kan vi regne ut stigningstallet.

$\begin{matrix} stigningstallet & = \frac{f (210) - f (90)}{210 - 90} \\ = \frac{830, 3 - 3658, 7}{120} = - 23, 57 . \end{matrix}$

Oppgave 6 (4 poeng) Nettkode: E-4B36

Et flytende rengjøringsmiddel skal blandes med vann i forholdet 3 : 10

Du skal lage 6,5 dL ferdig blanding.

a)

Hvor mye rengjøringsmiddel og hvor mye vann trenger du?

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

At noe skal blandes i forholdet $3 : 10$ , betyr at vi skal ha 3 deler med den ene tingen til 10 deler av det andre. For eksempel kan vi blande 3 dL rengjøringsmiddel med 10 dL vann for å få 13 dL rengjøringsmiddel.

Det finnes en måte å gjøre dette på som alltid fungerer, men akkurat her kan vi ta en snarvei. Vi skal ha $6, 5$ dL rengjøringsmiddel, og det er nøyaktig halvparten av 13 dL, så vi kan halvere mengden vi bruker til $\frac{3}{2} dL = 1, 5 dL$ rengjøringsmiddel og $\frac{10}{2} dL = 5 dL$ vann.

Dette var én måte å gjøre det på, men vi er ikke alltid så heldig med tallene som vi har vært. Noen ganger må vi gjøre det mer generelt. Hvis vi skal blande i forholdet $3 : 10$ , så betyr det at vi har totalt $3 + 10 = 13$ deler, hvorav 3 skal være rengjøringsmiddel og 10 skal være vann. Det betyr at $\frac{3}{13}$ av totalvolumet skal være rengjøringsmiddel og $\frac{10}{13}$ skal være vann. Vi skal ha totalt $6, 5 dL$ – da må $\frac{3}{13} \cdot 6, 5 dL = 1, 5 dL$ av dette være rengjøringsmiddel. Resten skal være vann, og vi skal ha totalt $6, 5 dL$ , så $6, 5 dL - 1, 5 dL = 5 dL$ må være vann. Det er det samme som vi fikk tidligere.

Svar: $1, 5 dL$ rengjøringsmiddel og $5 dL$ vann.

Mer om

Denne oppgaven handler om

Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.

Brøk kan sees som et tall på tallinja eller som del av en mengde.

brøk

med

Teller

Tallet eller uttrykket som står over brøkstreken i en brøk.
Telleren forteller hvor mange brøkdeler som skal telles med.

Eksempel: I brøken $\frac{5}{9}$ , er det 5 som er telleren. 9 kalles nevner.

teller

Nevner

Tallet som står under brøkstreken i en brøk.
Nevneren forteller hvor mange like deler det hele er delt opp i.

Eksempel : $\frac{3}{7}$ . Tallet 7 er nevneren.

nevner

For flere eksempler og forklaringer på målinger og forhold mellom to ting, se lynkurset Målingsforhold, og for å teste dine brøkkunnskaper, se lynkurset Brøk.

b)

Oda har blandet rengjøringsmiddelet med vann i forholdet 3 : 8. Hun har en bøtte med 6,6 L av denne blandingen.

Hva kan hun gjøre for å få riktig blandingsforhold i bøtta?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi observerer at Oda har brukt for lite vann, og da må hun tilsette mer for å få riktig blandingsforhold. Det er lurt av oss å først finne ut hvor mange desiliter rengjøringsmiddel det er i Odas blanding. Deretter kan vi regne ut hvor mye vann som egentlig skal være med i en slik blanding.

Vi må tilsette litt mer vann. For å finne ut hvor mye, må vi finne ut hvor mye rengjøringsmiddel det er i blandingen. Vi har totalt $3 + 8 = 11$ deler blanding, der 3 deler er rengjøringsmiddel. Det riktige forholdet er $3 : 10$ , så vi skulle egentlig hatt 2 deler vann til. Alle de 11 delene av blandingen utgjør $6, 6 dL$ , og 1 del av dette er $\frac{6, 6 dL}{11} = 0, 6 dL .$ Vi skulle ha 2 deler med vann til, altså $2 \cdot 0, 6 = 1, 2 dL$ , så Oda må tilsette $1, 2 dL$ vann til blandingen.

Svar: Oda kan tilsette $1, 2 dL$ vann til blandingen.

Mer om

Denne oppgaven handler om

Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.

Brøk kan sees som et tall på tallinja eller som del av en mengde.

Brøk

med

Teller

Nevner

Tallet som står under brøkstreken i en brøk.
Nevneren forteller hvor mange like deler det hele er delt opp i.

Eksempel : $\frac{3}{7}$ . Tallet 7 er nevneren.

Nevner

For flere eksempler og forklaringer på målinger og forhold mellom to ting, se lynkurset Målingsforhold, og for å teste dine brøkkunnskaper, se lynkurset Test deg selv i brøk!.

Oppgave 7 (2 poeng) Nettkode: E-4B39

På et bilde er en bakterie $2$ cm lang. I virkeligheten er bakterien $20 μ m$ lang.

$1 μ m = 10^{- 6} m$

Bestem målestokken til bildet.

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi må finne ut hvor mye én centimeter i virkeligheten blir på bildet.

Målestokken til et bilde er hvor mange centimeter én centimeter på bildet er i virkeligheten, eller tilsvarende $målestokk = \frac{lengde på bildet}{lengde i virkeligheten} .$ På bildet er $2 cm$ det samme som $20 μ m$ i virkeligheten. Vi husker at $1 μ$ m $= 10^{- 6}$ m og $1 cm = 0, 01$ m, så målestokken blir $\frac{20 \cdot 10^{- 6} m}{0, 02 m} = 1 000 .$ Det betyr at målestokken er $1 000 : 1$ .

Svar: $1 000 : 1$

Mer om

Denne oppgaven handler om

Målestokk

Målestokken angir hva en måleenhet på for eksempel kartet svarer til i terrenget.

Eksempel:
Et kart har målestokken 1 : 25000 (leses: en til tjuefemtusen)

Dette betyr for eksempel at:

-	1 cm på kartet tilsvarer 25000 cm i terrenget (25000 cm = 250 m)
-	1 dm på kartet tilsvarer 25000 dm i terrenget
-	4 cm på kartet er 25000 · 4 cm i terrenget (25000 · 4 cm = 100000 cm = 1000m = 1 km).

Eller mer generelt:
1 bestemt måleenhet på kartet er 25000 slike måleenheter i terrenget.

målestokk

, og

Brøk

Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.

Brøk kan sees som et tall på tallinja eller som del av en mengde.

brøk

med

Teller

teller

Nevner

Tallet som står under brøkstreken i en brøk.
Nevneren forteller hvor mange like deler det hele er delt opp i.

Eksempel : $\frac{3}{7}$ . Tallet 7 er nevneren.

nevner

For flere eksempler og forklaringer på målestokk, se lynkurset Målestokk.

For å øve mer, se oppgavesettet om målestokk i Treningsleieren.

Oppgave 8 (7 poeng) Nettkode: E-4B3C

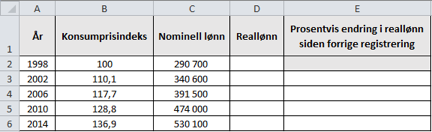
Jostein vil ha en oversikt som viser hvordan reallønnen hans har endret seg.

a)

Lag et regneark som vist ovenfor. Når Jostein har registrert konsumprisindeks og nominell lønn, skal han få beregnet reallønn. Han skal også få beregnet hvor mange prosent reallønnen har endret seg siden forrige registrering.

Løs oppgaven her

Løsningsforslag a)

Jeg tenker

Regneark finner vi i flere programmer. Vi velger her å bruke Excel. Vi må finne ut hvordan vi regner reallønnen ved hjelp av Excels funksjoner.

Først lager vi et tilsvarende regneark som i oppgaven.

	A	B	C	D	E
1	År	Konsumpris- indeks	Nominell lønn	Reallønn	Prosentvis endring
2	1998	100
3	2002	110,1
4	2006	117,7
5	2010	128,8
6	2014	136,9

Deretter skal vi regne ut reallønn. Husk at vi har følgende formel gjeldende reallønn: $\frac{reallønn}{100} = \frac{lønn}{indeks}$ Vi vil regne ut reallønnen, så det hadde vært en fordel å få reallønnen alene på venstre side. Derfor multipliserer vi med 100 på begge sider av likhetstegnet, og får $reallønn = 100 \cdot \frac{lønn}{indeks} .$ La oss først regne ut hva som er reallønnen i 1998 ved å bruke rutene i regnearket. Konsumprisindeksen står i rute B2 og nominell lønn står i rute C2, så reallønnen blir $100 \cdot \frac{C2}{B 2}$ . Derfor skriver vi

=100*C2/B2

i rute D2. Tilsvarende skal det som står i D3 være

=100*C3/B3

og så videre. Vi slipper å skrive ned alle sammen; de fleste regneark tillater at vi bare skriver det som skal stå i rute D2, og deretter at vi “drar” innholdet ned til rute D6. Nå blir regnearket seende slik ut.

	A	B	C	D	E
1	År	Konsumpris- indeks	Nominell lønn	Reallønn	Prosentvis endring
2	1998	100	290700	290700
3	2002	110,1	340600	309355
4	2006	117,7	391500	332625
5	2010	128,8	474000	368012
6	2014	136,9	530100	387216

Til slutt skal vi regne ut hvor mange prosent reallønnen har endret seg siden forrige registrering. I 1998 har vi ingen tidligere registrering, så vi starter med 2002. Vi må altså regne ut hvor mye reallønnen har endret seg fra 1998 til 2002. Vi starter med å finne ut hvor mange prosent lønnen i 2002 er av lønnen i 1998. Den finner vi ved å ta forholdet mellom de to og multiplisere med 100 %. Med tall: $100 % \cdot \frac{lønn i 2002}{lønn i 1998} = 100 % \cdot \frac{309355}{290700} \approx 106, 4 % .$ Lønnen i 2002 er altså rundt $106, 4 %$ av lønnen i 1998. Det betyr at lønnen har endret seg med $106, 4 % - 100 % = 6, 4 %$ fra 1998 til 2002. Vi skal gjøre dette i rute E3 i regnearket, og alt vi trenger å gjøre er å erstatte variablene som forekommer i ([d2eq8a]) med deres rutenavn og trekke fra 100. Med andre ord erstatter vi “lønn i 2002” med D3, og “lønn i 1998” med D2. Dermed blir endringen i prosent lik $100 \cdot \frac{D3}{D2} - 100$ , eller $100 \cdot (\frac{D3}{D2} - 1) = \frac{D3 - D2}{D2} \cdot 100$ . Vi skriver følgende inn i E3:

=100*D3/D2 - 100

Vi kunne også ha skrevet

=(D3-D2)/D2*100

Igjen kan vi “dra” ruten ned til rad 6, og til slutt ser regnearket slik ut:

	A	B	C	D	E
1	År	Konsumpris- indeks	Nominell lønn	Reallønn	Prosentvis endring
2	1998	100	290700	290700
3	2002	110,1	340600	309355	64
4	2006	117,7	391500	332625	75
5	2010	128,8	474000	368012	106
6	2014	136,9	530100	387216	52

Svar:

	A	B	C	D	E
1	År	Konsumpris- indeks	Nominell lønn	Reallønn	Prosentvis endring
2	1998	100	290700	290700
3	2002	110,1	340600	309355	6,4
4	2006	117,7	391500	332625	7,5
5	2010	128,8	474000	368012	10,6
6	2014	136,9	530100	387216	5,2

Mer om

Denne oppgaven er om reallønn,

Prosent

Prosent betyr hundredel og skrives %.

Eksempel: Hvor mange prosent er 1 av 4? $\frac{1}{4} = \frac{1 \cdot 25}{4 \cdot 25} = \frac{25}{100} = 25 %$ .

Prosent

, og

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

Likning

For flere eksempler og forklaringer på prosent, se lynkurset Hva er prosent?, og for likninger se lynkurset Hva er en likning? .

Lynkurset om bruk av regneark er under utarbeidelse og kommer snart.

b)

Anta at konsumprisindeksen øker med 2,5 % per år i perioden fra 2014 til 2024.

Hva må Josteins nominelle lønn i 2024 være dersom han da skal få en reallønn som er 10 % høyere enn reallønnen i 2014?

Løs oppgaven her

Løsningsforslag b)

Jeg tenker

Vi må regne ut

Konsumprisindeks

(hentet fra http://snl.no/konsumprisindeks)

konsumprisindeksen

i 2024.

Husk at vi har følgende formel. Den benyttes så å si alltid når vi skal regne ut noe med nominell lønn eller reallønn. $\frac{reallønn}{100} = \frac{lønn}{indeks}$ Vi vil at Josteins reallønn skal være $10 %$ høyere i 2024 enn i 2014. Nå kan vi multiplisere lønnen i 2014 med 11 og sette inn i likningen ovenfor, men det lønner seg ofte å sette inn tallene vi vet om til slutt. La $x$ være Josteins nominelle lønn i 2024, og la $y$ være reallønnen i 2014. Vi vil at Josteins reallønn skal være $10 %$ høyere i 2024 enn i 2014, med andre ord at den skal være lik $y + y \cdot 10 % = 1, 1 \cdot y$ . Vi setter dette inn i likningen $\frac{reallønn}{100} = \frac{lønn}{indeks}$ , og får $\frac{1, 1 \cdot y}{100} = \frac{x}{indeks} .$ Vi vil finne ut hva $x$ er, så vi multipliserer med indeksen på begge sider av likhetstegnet. $x = \frac{1, 1 \cdot y}{100} \cdot indeks$ I likningen over vet vi allerede hva $y$ er, og vi vil finne ut hva $x$ er. Derfor vil vi finne konsumprisindeksen i 2024. Den øker med $2, 5 %$ per år fra 2014, så i 2015 blir den $136, 9 + 136, 9 \cdot 2, 5 % = 136, 9 \cdot 1, 025 \approx 140, 3$ . For å finne indeksen i 2016 må vi igjen multiplisere med $1, 025$ , og det samme må vi gjøre for å finne indeksen i 2017. Får å finne indeksen i 2024 må vi altså multiplisere 10 ganger med $1, 025$ . Derfor blir indeksen lik $136, 9 \cdot 1, 025^{10} \approx 175, 24 .$ Vi setter dette inn i $x = \frac{1, 1 \cdot y}{100} \cdot indeks$ Husk at $y =$ reallønn i 2014 = 387216, så får at den nominelle lønnen i 2024 må være $x = \frac{1, 1 \cdot 387216}{100} \cdot 175, 24 \approx 746415 .$

Svar: Cirka 746415 kroner.

Mer om

Denne oppgaven er om

Konsumprisindeks

(hentet fra http://snl.no/konsumprisindeks)

konsumprisindeks

Prosent

Prosent betyr hundredel og skrives %.

Eksempel: Hvor mange prosent er 1 av 4? $\frac{1}{4} = \frac{1 \cdot 25}{4 \cdot 25} = \frac{25}{100} = 25 %$ .

prosent

, og

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likninger

For flere eksempler og forklaringer om prosent, se lynkurset Prosent, og for likninger se lynkurset Likning.

Lynkurset om konsumprisindeks er under utarbeidelse og kommer snart.

Oppgave 9 (2 poeng) Nettkode: E-4B3F

En vanntank har form som en sylinder. Tanken er 0,8 m høy og rommer 150 L.

Bestem radius i tanken.

Løs oppgaven her

Løsningsforslag

Jeg tenker

Vi kan bruke

Formel

En formel i matematikk er en måte å uttrykke sammenhenger på, skrevet i et symbolsk språk.

Eksempel: $A = π r^{2}$ , er en formel for flateinnholdet av en sirkel med radius r.

formelen

for

Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm³) og kubikkmeter (m³).

volumet

av en

Sylinder

En sylinder er en tredimensjonal figur. En vanlig sylinder er satt sammen av to identiske sirkler og et rektangel.

sylinder

. Vi husker også at 1 L

= 1

^{3}

1

^{3} = 1 000

Husk at volumet $V$ til en sylinder med radius $r$ og høyde $h$ er lik $V = h \cdot π \cdot r^{2} .$ Vi kan også komme fram til dette ved å huske at arealet til en sirkel med radius $r$ er $π \cdot r^{2}$ , og at vi kan multiplisere med høyden $h$ for å få volumet av sylinderen med sirkelen som grunnflate. Fra oppgaveteksten har vi at $h = 0, 8$ m og $V = 150$ L. Vi setter dette inn i ligningen over. $150 L = 0, 8 m \cdot π \cdot r^{2}$ Vi vil finne en $r$ som passer inn i ligningen over, så vi dividerer med $0, 8 m \cdot π$ på begge sider av likhetstegnet. Da får vi $r^{2} = \frac{150 L}{0, 8 m \cdot π} .$ Nå har vi funnet $r^{2}$ , men vi vil ha tak i $r$ , så vi må ta kvadratroten av begge sider over. $\sqrt{r^{2}} = r = \sqrt{\frac{150 L}{0, 8 m \cdot π}}$ Her kan det være fristende å regne ut $\sqrt{150 / (0, 8 \cdot π)}$ , men vi må passe på. Et varseltegn er at vi ikke har noen pen måleenhet på det som står under kvadratroten. Husk at 1 kubikkmeter er det samme som 1000 liter, så $150 L = \frac{150}{1000} m^{3} = 0, 15 m^{3} .$ Hvis vi setter dette inn i ligningen over, så får vi $r = \sqrt{\frac{0, 15 m^{3}}{0, 8 m \cdot π}} = \sqrt{\frac{0, 15}{0, 8 \cdot π} m^{2}} = \sqrt{\frac{0, 15}{0, 8 \cdot π}} m .$ Denne måleenheten passer seg bedre for en radius. Vi taster inn på kalkulatoren og får at $r \approx 0, 2443$ m = $24, 43 cm$ .

Svar: Cirka $24, 43 cm$ .

Mer om

Oppgaven handler om

Volum

Volum er et måltall som uttrykker tredimensjonal utstrekning i rommet (bredde, lengde og høyde). Volum er målt i kubikkenheter, som foreksempel kubikkcentimeter (cm³) og kubikkmeter (m³).

volum

Sylinder

En sylinder er en tredimensjonal figur. En vanlig sylinder er satt sammen av to identiske sirkler og et rektangel.

sylinder

Pi (π)

$π$ er forholdet mellom sirkelens omkrets og diameter. Dette forholdet er alltid konstant og tilnærmet lik 3,14.

Kvadratrot

Kvadratrot har symbolet $\sqrt{}$ .

Kvadratroten av et tall a er et tall b, som multiplisert med seg selv gir a.

Kvadratroten av et positivt tall, for eksempel 16, er det positive tallet som multiplisert med seg selv gir 16. Kvadratroten av 16 er 4, fordi $4 \cdot 4 = 16$ . Det skrives $\sqrt{16} = 4$ .

kvadratrot

Ligning

En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.

Eksempel: $2 x + 8 = 14$

likninger

Formel

En formel i matematikk er en måte å uttrykke sammenhenger på, skrevet i et symbolsk språk.

Eksempel: $A = π r^{2}$ , er en formel for flateinnholdet av en sirkel med radius r.

formeler

For flere eksempler og forklaringer på volum, se lynkurset Volum, for sylindere, se artikkelen En sylinder. For flere forklaringer og eksempler om likninger, se lynkurset Likninger med én ukjent. For eksempler og forklaringer om regneregeler med kvadratrøtter, se lynkurset Kvadratrot.

For å øve mer, se oppgavesettet om volum i Treningsleieren.

Visste du at

Et sylinder er mange sirkel plater lagt oppå hverandre, et uendelig antall sirkel plater faktisk. Dette kan man se hvis man sammenligner formlen for areal av en sirkel og formelen for volum av et sylinder. Arealet av en sirkel er,

$A = π \cdot r^{2}$

Og volumet av et sylinder er,

$V = π \cdot r^{2} \cdot h$

For å virkelig bevise dette må man bruke integrasjon, men for nå kan vi bare se at det er en sammenheng, og huske at volumet av et sylinder er arealet av en sirkel multiplisert med høyden av sylinderet.

MAT1011 2015 Vår

Del 1

Del 2

Eksamensinformasjon

DEL 1 Uten hjelpemidler

Oppgave 1 (1 poeng) Nettkode: E-4AZI

a)

Løsningsforslag a)

Desimaltall

Multiplikasjon

Prosentfaktor

Prosent

Prosentfaktor

Desimaltall

b)

Løsningsforslag b)

Nevner

Multiplikasjon

Prosent

Brøk

Desimaltall

Oppgave 2 (2 poeng) Nettkode: E-4AZM

a)

Løsningsforslag a)

Trekant

Vinkelsum

Trekant

Toppvinkler

Vinkelsum

Formlike trekanter

b)

Løsningsforslag b)

Formlike trekanter

Proporsjon

Formlike trekanter

Trekant

Ligning

Oppgave 3 (2 poeng) Nettkode: E-4AZP

Løsningsforslag

Kvadrat

Pytagoras læresetning

Kvadrat

Trekant

Pytagoras læresetning

Oppgave 4 (2 poeng) Nettkode: E-4AZX

Løsningsforslag

Trekant

Areal

Rektangel

Rektangel

Trekant

Areal

Oppgave 5 (4 poeng) Nettkode: E-4B03

a)

Løsningsforslag a)

Funksjon

Andregradsuttrykk

b)

Løsningsforslag b)

Koordinatsystem

Funksjon

Graf

Oppgave 6 (3 poeng) Nettkode: E-4B0B

a)

Løsningsforslag a)

Sannsynlighet

Sannsynlighet

b)

Løsningsforslag b)

Sannsynlighet

Sannsynlighet med tilbakelegging

Produktsetningen

Addisjonssetningen

Oppgave 7 (2 poeng) Nettkode: E-4B0F

Løsningsforslag

Konsumprisindeks

Konstant

Konsumprisindeks

Oppgave 8 (3 poeng) Nettkode: E-4B0J

a)