Graftegner
Med graftegneren kan vi enkelt visualisere funksjoner. Ofte er det enklere å se på en graf for å forstå problemet enn å se på funksjonsuttrykket. Graftegneren er derfor det viktigste verktøyet og hvis man behersker den godt, så kan mange problemer bli mye lettere å forstå og å løse.
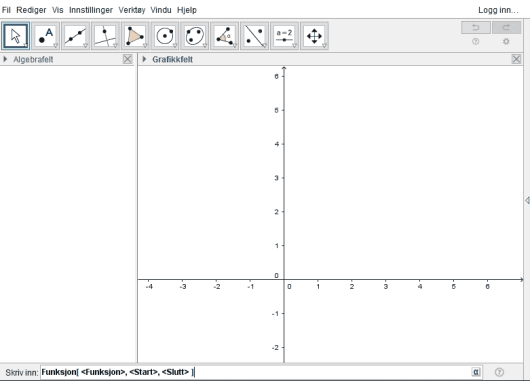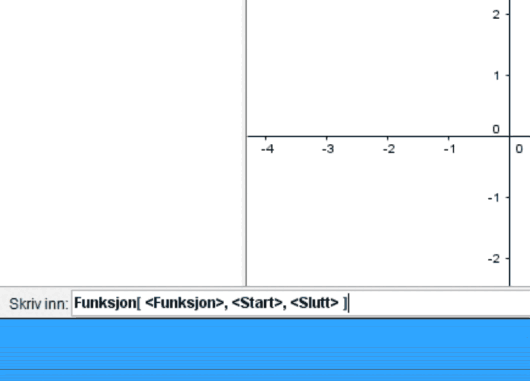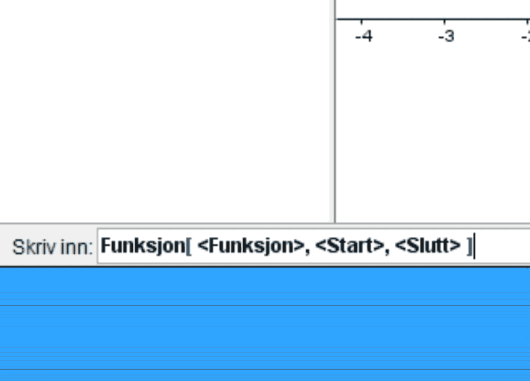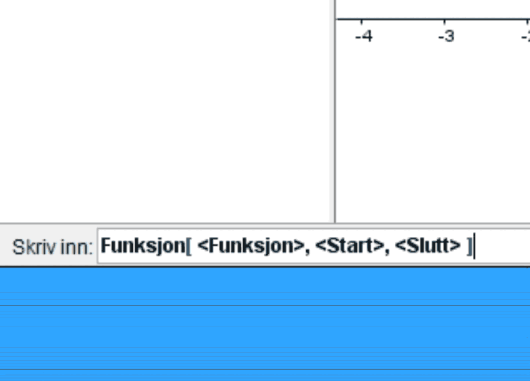
Under har vi et skjermbilde av graftegneren i GeoGebra. Helt nederst i bilde er inntastingsfeltet. Det er der vi skal skrive inn funksjonene for å få dem tegnet. Skriver du inn noe der så får du mange forslag. Vi har valgt forslaget Funksjon[ Funksjon, Start, Slutt ], som vil tegne en graf for oss. Vi må bytte ut Funksjon med funksjonsuttrykket, og Start og Slutt med og .
Eksempel 1
En varm julidag var temperaturen mellom kl. og kl. gitt, i , ved , hvor er antall timer etter kl. .
Vi skal tegne grafen til til slik at den viser temperaturene mellom kl. og kl. .
Da kan vi bruke kommandoen Funksjon[Funksjon, Start, Slutt]. er antall timer etter kl. , så når vi skal tegne funksjonen vil vi ha som startverdi, og som sluttverdi. Da vil grafen vise temperaturene mellom kl. og . Vi vil at funksjonen skal hete T, og dette definerer vi ved å skrive “T(x):=”.
Når vi skal skrive potensuttrykk i GeoGebra bruker vi ^ før eksponenten, så skal vi for eksempel skrive skriver vi "x^2". For å tegne grafen til funksjonen vår skriver vi T(x):=Funksjon[-0.27x^2+3x+18,0,12].
Det går også an å skrive funksjonen direkte inn ved å skrive
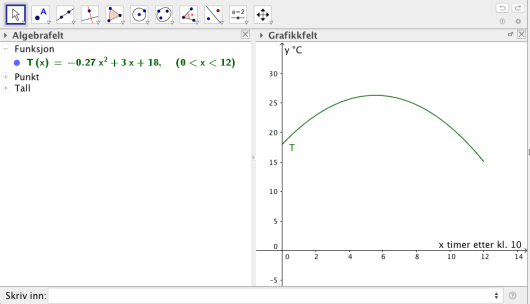
T(x):=-0.27x^2+3x+18, 0<x<12.
Da vil får vi følgende graf.
Vi kan også bruke GeoGebra til for eksempel å finne når på dagen det var varmest. Da vil vi finne maksimumsverdien til . Det kan vi gjøre ved kommandoen Maks[<Funksjon>, <Start>, <Slutt>], så da kan vi skrive Maks[T, 0, 12] som gir oss punktet . Dette forteller oss at det var varmest omtrent timer etter kl. , altså rundt kl , og da var temperaturen på ca .
Eksempel 2
Selskapet ’Ski for alle!’ selger ski og har et mål om å selge par ski.
For hver par ski som blir laget og fraktet til butikken, har vi kostnadene gitt ved .
Et par ski blir solgt for kr, og da får vi salgspris-funksjonen, .
Profitt per ski solgt til ’Ski for alle!’ selskapet er da gitt ved .
Vi skal tegne alle tre grafene og se hvordan selskapet utvikler seg.
Vi tegner først kostnadsfunksonen fra til . Dette setter vi inn i Funksjon[ Funksjon, Start, Slutt ]. Vi vil også at kostnadsfunksjonen skal hete og det kan vi gjøre ved å legge til K(x):= foran Funksjon[ Funksjon, Start, Slutt ].
For å skrive inn funksjonsuttrykket til må vi da skrive "5000e^(-x/100)+1000" for <Funksjon>. Hele kommandoen skriver vi slik:
K(x):=Funksjon[5000e^(-x/100)+1000, 0 , 1000]
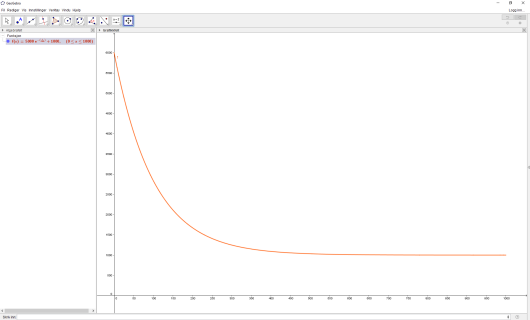
Da får vi grafen
Vi ser her at jo flere ski som blir laget, jo mindre blir produksjonskostnadene per par ski. Dersom de lager par ski så koster det ca kr å lage og frakte et par ski.
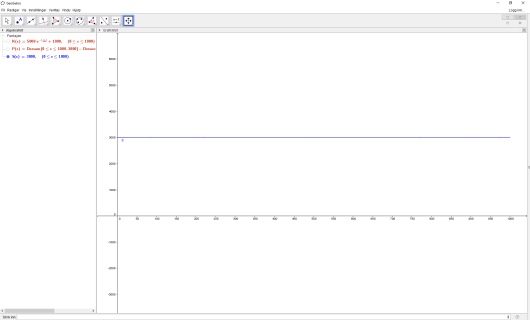
La oss nå se på hvordan salgsfunksjonen utvikler seg. Igjen tegner vi grafen fra til , og vil at salgspris-funksjonen skal hete : Da skriver vi inn S(x):=[3000x,0,1000]
Her er salgspris-funksjonen bare en rett linje fordi prisen forandrer seg ikke. Selskapet har valgt å selge skiene for kr uansett hvor mange eller hvor få ski de produserer.
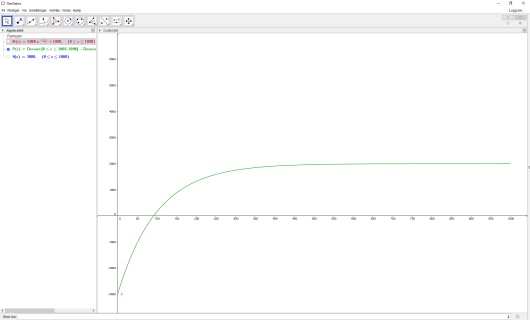
Til slutt tegner vi profittfunksjonen. Vi definerte den som , og vi kan da skrive dette direkte inn i inntastingsfeltet nederst i graftegneren. Alt vi trenger å skrive er P(x):=S(x)-K(x), og får da:
Vi ser her at hvis selskapet produserer og selger mer enn par ski vil de tjene penger på skiene som blir solgt. Men hvis de produserer og selger par ski, vil de tjene ca. kr per par ski som blir solgt.
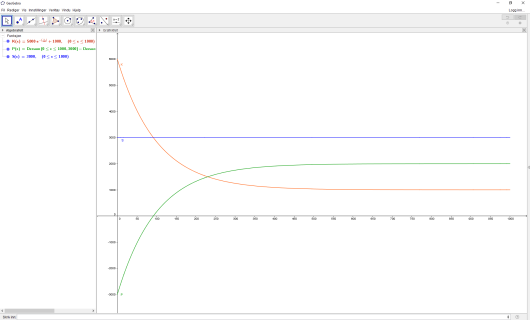
Vi kan se alle tre grafene i samme koordinatsystem også. Til venstre side står våre tre funksjoner. Vi må bare passe på at det er en blå sirkel ved siden av funksjonsuttrykket. Trykker vi på den blå sirkelen kan vi bestemme om en funksjon skal være synlig eller ikke.
Del på Facebook