Proporsjonalitet
Proporsjonalitet er et ord vi til vanlig bruker om ting som skal samsvare. I matematikken brukes ordet omtrent på samme måte, men som ofte ellers må vi være mer presise om hva vi mener.
Proporsjonale funksjoner
En proporsjonalitet er en bestemt type lineær funksjon, som skrives på formen
.
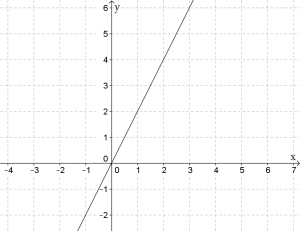
Dette er en lineær funksjon med konstantledd lik 0. Dermed vet vi at grafen til funksjonen er en rett linje som går gjennom origo, og at stigningstallet bestemmer hvor bratt funksjonsgrafen er. Et eksempel på en proporsjonalitet er , som vi har tegnet under.
Omvendt proporsjonale funksjoner
En proporsjonalitet er en funksjon der vi tar et tall og multipliserer det med en variabel . Hvis vi i stedet dividererer med , får vi det man kaller en omvendt proporsjonalitet. Det ser slik ut:
.
I motsetning til proporsjonaliteter, som bare var spesielle lineære funksjoner, er omvendt proporsjonale funksjoner en helt annen type funksjon. De får en bueform som vokser mot uendelig når nærmer seg 0, siden en brøk med konstant teller blir større jo mindre nevneren er.
Eksempel
Om vi velger får vi et eksempel på en omvendt proporsjonal funksjon, .
Om vi setter inn
får vi
.
Setter vi , får vi
.
Setter vi , får vi
.
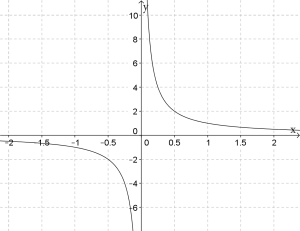
Dette viser ved eksempel at jo mindre er, jo større blir . Her har vi tegnet grafen til :
Hva er -verdien når ?
Del på Facebook
Lynkurs, 8.-10.trinn
Funksjoner (del I)
Består av:
- Hva er en funksjon?
- Koordinatsystem
- Fra en funksjon til en graf
- Rette linjer (lineære funksjoner)
- Proporsjonalitet
- Fra en graf til en funksjon
- Andregradsfunksjoner
- Funksjonsgrafer for andregradsfunksjoner
- Hvorfor ser grafen ut som den gjør?
- Inger Christin forteller om funksjoner.
- Test deg selv i lineære funksjoner!
- Test deg selv i funksjoner!
Begrep
-
Brøk
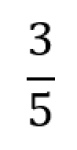
Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.
Brøk kan sees som et tall på tallinja eller som del av en mengde.
-
Divisjon
Divisjon er en regneart som er den omvendte operasjonen av multiplikasjon.
Eksempel: fordi .
-
Graf
En graf er en tegning av en funksjon i et koordinatsystem. Inn-verdi (x) og ut-verdi (y) i funksjonen danner et tallpar. Vi tegner tallparene fra funksjonen som punkter i koordinatsystemet, og trekker en sammenhengende strek mellom punktene.
-
Lineære ligninger
Ligninger der alle de ukjente opptrer i første grad.
Eksempel:
-
Multiplikasjon
Å multiplisere er det samme som gjentatt addisjon, ofte kalt "ganging".
Regneoperasjonen 3 · 4 = 12 kalles en multiplikasjon, og sier at vi skal legge sammen tallet 3 fire ganger, eller at vi skal ta tallet 4 og addere dette med seg selv 3 ganger.Produktet blir det samme, uansett hvilken rekkefølge faktorene kommer i.
Eksempel: 3 · 4 = 12 og 4 · 3 = 12
Tallene 3 og 4 kalles faktorer, og resultatet kalles et produkt.
Mellom faktorene skrives multiplikasjonstegn (·). -
Nevner
Tallet som står under brøkstreken i en brøk.
Nevneren forteller hvor mange like deler det hele er delt opp i.Eksempel : . Tallet 7 er nevneren.