Øvingsoppgaver med fasit
Lenke til dette oppgavesettet (kan bokmerkes)Oppgaver
1
Funksjonen har en tangent i punktet . Finn likningen for tangenten.
2
Hva beskriver den deriverte til en potensfunksjon?
3
Regn ut den gjennomsnittlige veksthastigheten for funksjonen når x er fra 2 til 2,01 og fra 2 til .
4
5
Finn den deriverte til .
6
Bruk definisjonen av den deriverte til å vise at har som derivert.
7
8
Finn en potensfunksjon og deriver den. Bruk den deriverte til å tegne grafen til potensfunksjonen.
9
Tangenten til kurven i punktet (1, -1) har stigningstall k = 4. Finn a og b.
10
Fasit
1
2
3
12,03 og
4
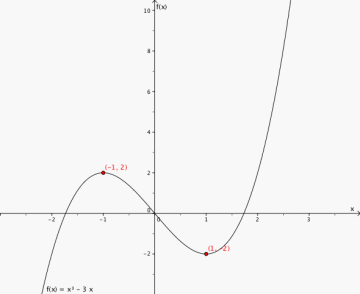
Toppunkt (-1,2)
Bunnpunkt (1,-2)
Grafen stiger når x<-1 og når x>1. Grafen synker når -1
5
6
Hint: multipliser både teller og nevner i med
7
8
9
a = 5, b = - 6
10
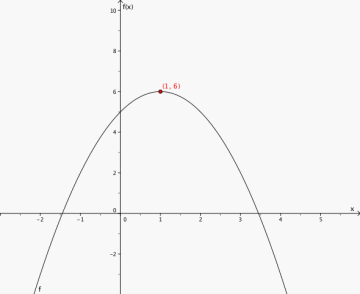
Toppunkt (1,6)
Grafen stiger når x<1
Grafen synker når x>1