Øvingsoppgaver med fasit
Lenke til dette oppgavesettet (kan bokmerkes)Oppgaver
1
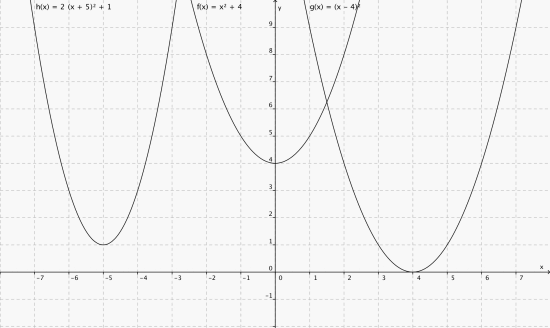
Finn symmetriaksene til grafene på bildet.
2
Vis uten regning at likningen har bare en løsning.
3
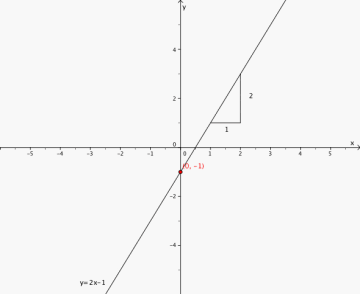
Utnytt konstantleddet og stigningstallet til å tegne linjen:
4
5
Populasjonen av maur i en tue, t uker etter oppdagelsen følger eksponentialfunksjonen
.
- Hvor mange maur var det i maurtuen når den ble oppdaget?
- Hvor mange maur er det i tuen etter 5 uker og etter 2 måneder?
- Når vil det være 2000 maur i tuen?
6
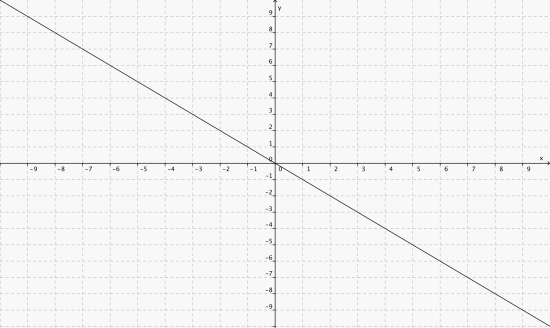
Finn en andregradsfunksjon som har grafen på bildet som symmetriakse.
7
Regn ut når . Tegn grafen til funksjonen og les av verdimengden.
8
Hva er verdimengden til funksjonen ?
9
Løs ligningssettet grafisk:
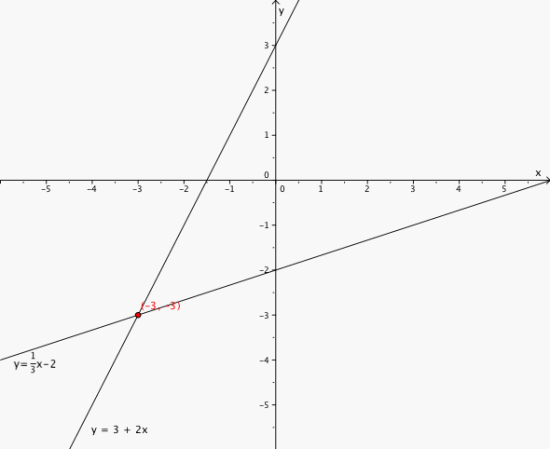
10
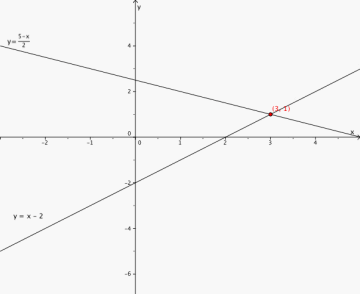
Løs ligningssettet grafisk:
Fasit
1
Fra venstre: x = - 5, y - aksen, x = 4.
2
Tegn grafen til funksjonen og da vil du se at grafen skjærer y - aksen på bare et sted,
3
Stigningstall: 2
Konstantledd: - 1
4
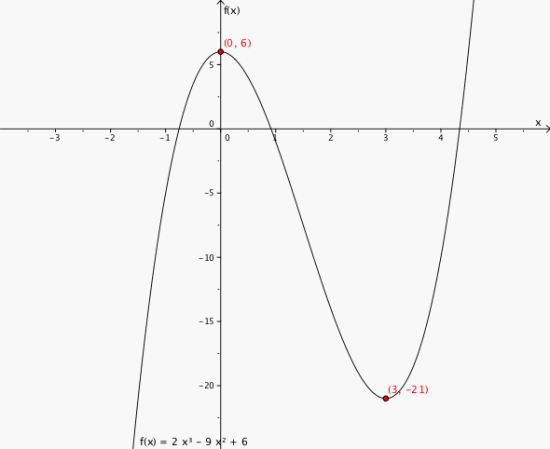
Toppunkt (0,6)
Bunnpunkt (3,-21)
Grafen stiger når x<0 og når x>3- Grafen synker når 0
5
- 400
- Etter fem uker er det 704 maur og etter 8 uker er det 990.
- Etter 14, 2 uker.
6
Finnes ikke.
7
, og
Verdimengden er
8
, alle relle tall større eller lik 1
9
x = -3 og y = -3
10
x = 3 og y = 1