Øvingsoppgaver med fasit
Lenke til dette oppgavesettet (kan bokmerkes)Oppgaver
1
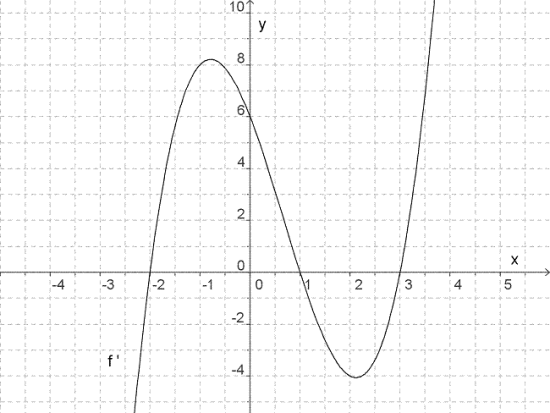
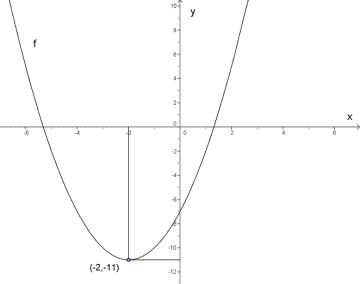
Grafen på figuren viser den deriverte til en funksjon .
a) Tegn fortegnsskjema. I hvilke intervaller stiger og synker grafen til ?
b) Bestem -koordinatene for topp- og bunnpunktene til .
2
Tegn grafen ved hjelp av et digitalt verktøy og finn koordinatene til eventuelle topp- og bunnpunkter for følgende funksjon:
3
Drøft funksjonene:
a)
b)
4
Tegn grafen til parabelen og les av eventuelle topp- og bunnpunkter:
5
Tegn grafen ved hjelp av et digitalt verktøy og finn koordinatene til eventuelle topp- og bunnpunkter for følgende funksjon:
6
f(x)
7
Finn ved regning koordinatene til eventuelle topp- og bunnpunkter for funksjonene nedenfor. Tegn deretter grafene ved hjelp av digitale verktøy og kontroller svarene.
a)
b)
c)
8
Tegn grafen til parabelen og les av eventuelle topp- og bunnpunkter:
9
10
Undersøk om funksjonen har topp- eller bunnpunkt. Oppgi koordinatene til punktet.
Fasit
1
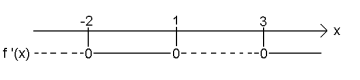
a)
avtar for og for .
stiger for og for .
b) Bunnpunkter: .
Toppunkt:
2
toppunkt:
bunnpunkt:
3
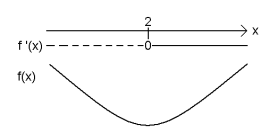
a)
synker for .
vokser for .
Bunnpunkt i .
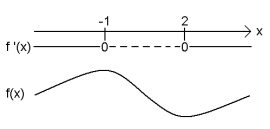
b)
synker for .
vokser for
og for .
Toppunkt i ,
bunnpunkt i .
4
toppunkt: (1, 4)
5
toppunkt:
bunnpunkt:
6
7
a) Bunnpunkt i .
b) Bunnpunkt i .
c) Toppunkt i , bunnpunkt i .
8
toppunkt: (-1, 4)
9
10
Funksjonen har et bunnpunkt, (0,-3).