Øvingsoppgaver med fasit
Lenke til dette oppgavesettet (kan bokmerkes)Oppgaver
1
La være funksjonen .
a) Finn nullpunktene til ved regning.
b) Finn funksjonens topp- og bunnpunkter ved regning.
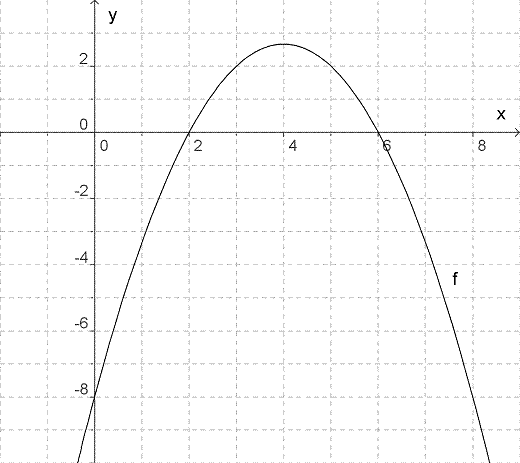
2
Figuren viser grafen til en funksjon . Svar på spørsmålene ved hjelp av figuren.
a) Hva er nullpunktene til ?
b) Hva er symmetriaksen?
c)
Finn verdiene av , og .
3
Gi et eksempel på en funksjon uten nullpunkter.
4
Er et av nullpunktene til ? Begrunn svaret.
5
Gi et eksempel på en rasjonal funksjon med et nullpunkt.
6
Hvilken likning må du løse for å finne nullpunktet til funksjonen ?
7
Forklar hvordan du finner nullpunktene til funksjonen .
8
Hvilke av funksjonene har et nullpunkt? Begrunn svaret.
9
Gi eksempel på en lineær funksjon som har et nullpunkt og en andregradsfunksjon som har to nullpunkter. Finn nullpunktene til disse funksjonene.
10
Fred påstår:"Når vi skal finne definisjonsområdet, må vi først finne nullpunkt til en funksjon." Kommenter påstanden.
Fasit
1
a)
b) Bunnpunkter: , toppunkt:
2
a)
b)
c)
3
4
Nei, i det punktet er funksjonen ikke definert.
5
6
7
8
Den eneste funksjonen som har et nullpunkt er h(x).