Øvingsoppgaver med fasit
Lenke til dette oppgavesettet (kan bokmerkes)Oppgaver
1
Funksjonen f gitt ved
der x skal være mellom 0 og 10.
a) Finn .
b) Hvilken x - verdi gir minst f(x)?
c) Hva er definisjons- og verdimengden i denne problemstillingen?
2
Hvilke punkter på har en tangent med stigningstallet 216?
3
La være funksjonen .
a) Hva er stigningstallet til tangenten til grafen i ?
b) Hva er stigningstallet til tangenten til grafen i ?
c) Finn likningen til tangenten i .
4
5
La være funksjonen .
a) Hvorfor kan man med en gang se at grafen til går gjennom origo?
b) Hvilke andre nullpunkter har ?
c) Finn topp- og bunnpunktene til .
6
Finn den deriverte til .
7
Den deriverte til en funksjon er null i punktene . Gi to ulike forslag til hvordan grafen kan se ut. Skisser grafene.
8
Tegn grafen til funksjonen . Finn stigningstallet til tangenten til kurven i punktet (1,2).
9
Deriver uttrykket:
10
Finn den deriverte for x = 2.
Fasit
1
a) - 300
b) og
c)D=[0,10]
d) V=[20195, 25000]
2
(6, 432) og (-6, -432)
3
a)
b)
c)
4
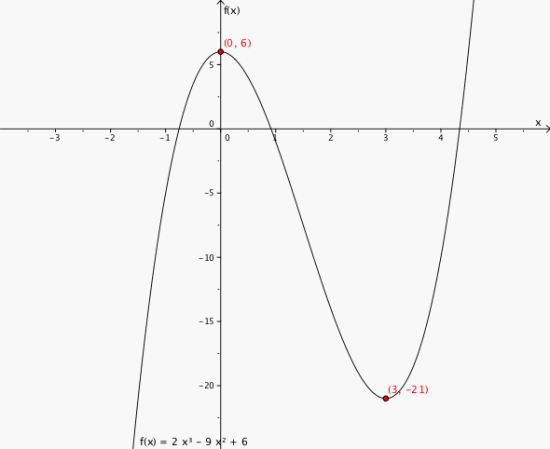
Toppunkt (0,6)
Bunnpunkt (3,-21)
Grafen stiger når x<0 og når x>3- Grafen synker når 0
5
a) , siden alle ledd inneholder .
b)
c) Bunnpunkt:
Toppunkt:
6
7
8
1
9
10
24