Platonske legemer
Hva er spesielt med platonske legemer, og hvorfor er det bare fem forskjellige?
I artikkelen "Regulære mangekanter" kan vi lese at summen av vinklene i en plan mangekant med n kanter er .
Dette resultatet tar vi med oss når vi nå tar et steg videre og ser på romlige figurer eller legemer. Et polyeder er et romlig legeme som er avgrenset av mangekanter. En terning eller en pyramide er eksempler på polyedre. Navnet polyeder kommer fra gresk og har to deler: poly som betyr mange og eder som kommer fra hedron og betyr side eller flate. Tilsvarende er det greske ordet for mangekant polygon der gon betyr kant. Det er mange romlige figurer som er avgrenset av mangekanter, så vi må presisere litt hva vi vil mener med et polyeder. For det første kaller vi mangekantene som avgrenser polyederet for sideflater. En terning har kvadratiske sideflater, seks stykker i alt. Siden sideflatene er mangekanter har de mange kanter eller sidekanter. Disse kalles også kanter for polyederet, og hver slik sidekant er kant i nøyaktig to sideflater. Endepunktene til en kant er et hjørne i polyederet. Der møtes tre eller flere sideflater. I terningen møtes tre kvadratiske sideflater i hver av de åtte hjørnene.
Alle sideflatene som møtes i et hjørne er mangekanter og har kantvinkel i dette hjørnet. I et hjørne på terningen møtes tre kvadratiske sideflater. Kantvinkelen til hver av disse i dette hjørnet er 90º. Summen av de tre kantvinklene i hjørnet er 270º. I et hjørne på et polyeder kan vi tilsvarende summere kantvinklene til mangekantene som møtes der. En sideflate er et plant område, så hver sideflate er del av et plan. Hjørnet i polyederet ligger enten helt på den ene siden av dette planet, eller så skjærer dette planet hjørnet i to. Hjørnet er konvekst dersom ingen av planene til sideflatene skjærer hjørnet i to, det vil si at hele hjørnet ligger på den ene siden av planet til hver sideflate. Når sidekantene folder seg (som i et trekkspill) er hjørnet ikke konvekst.
Dette er mulig dersom det er mer enn tre sideflater inn i hjørnet, og jo flere sideflater jo lettere er det å lage hjørner som ikke er konvekse. Dersom en lager et stjerneformet polyeder vil en ha hjørner som ikke er konvekse. I terninger, pyramider og prismer er derimot alle hjørnene konvekse. Et konvekst polyeder er et polyeder der alle hjørnene er konvekse. Vi skal stort sett behandle konvekse polyedre, og da vil følgende setning stå helt sentralt:
I et konvekst hjørne er summen av alle kantvinklene mindre enn 360º.
Det er ikke så vanskelig å se at denne setningen er riktig. Prøv å finne en god grunn for at dette er rett!
Et platonsk legeme er et et regulært polyeder. Det vil si at tilsvarende som for de regulære mangekantene, er alle sideflatene like, alle kantene like og alle hjørnene like. Dette betyr for eksempel at alle sideflatene er regulære mangekanter av samme slag og at polyederet er konvekst. Vi skal nå se på hvilke muligheter det er for slike platonske legemer. Dette skal vi gjøre ved å se bare på hjørnene. Husk at i et hjørne møtes minst tre sideflater og at summen av kantvinklene i et hjørne er mindre enn 360º. Hvis summen er 360º blir hjørnet flatt, og hvis summen er mer enn 360º blir det et foldet hjørne som ikke er konvekst.
Først undersøker vi om det fins platonske legemer som er slik at alle sideflatene er trekanter. Siden kantvinkelen i en trekant er 60º, kan tre, fire eller fem trekanter danne sideflater som møtes i et hjørne. Med seks trekanter er summen av kantvinklene 360º, så det går ikke.
Tre, fire, fem og seks trekanter inn i et hjørne.
Med tre trekanter i et hjørne, vil de tre kantene på disse sideflatene som ikke møtes i hjørnet danne en ny trekant. Tilsammen vil disse fire trekantene danne en trekantet pyramide, med fire sideflater, seks kanter og fire hjørner. Alle sideflatene er like, alle kantene er like og alle hjørnene er like, så pyramiden danner et platonsk legeme. Det kalles et tetraeder, siden det har fire sideflater og tetra betyr fire.
Tetraeder
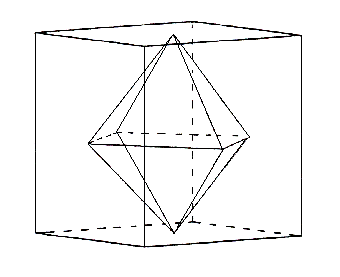
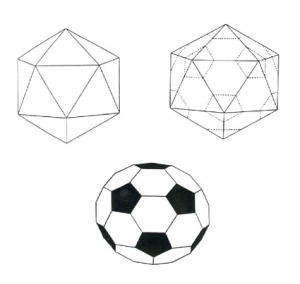
Det fins platonske legemer med fire og fem trekanter inn i hvert hjørne også. De kalles oktaeder og ikosaeder, siden de har åtte respektivt tyve sideflater hver, og okta betyr åtte mens ikosa betyr tyve. Disse er litt vanskeligere å se for seg. Oktaederet er en firkantet dobbelpyramide, mens ikosaederet er mer komplisert. Men med plastbrikker, eller pappbrikker er det ikke så vanskelig å bygge dem når en bare passer på at det skal være fire og fem trekanter i hvert hjørne.
| Oktaeder | Ikosaeder |
Dersom alle sideflatene er regulære firkanter, altså kvadrater, er det bare mulig å ha tre sideflater inn i hvert hjørne. Med fire kvadrater inn i et hjørne ville nemlig summen av kantvinklene bli 360º, så hjørnet ville bli flatt. Et polyeder med tre kvadrater som sideflater inn i hvert hjørne har vi allerede sett, nemlig terningen. Denne kalles også kube eller heksaeder siden den har seks sideflater og heksa betyr seks. Alle sideflatene, kantene og hjørnene er like så dette er et platonsk legeme.
Heksaeder, kube eller terning.
Dersom alle sideflatene er regulære femkanter, er det bare mulig å ha tre sideflater inn i hvert hjørne. Det fins et platonsk legeme som bare har slike hjørner. Det har 12 sideflater tilsammen, og kalles dodekaeder siden dodeka betyr tolv. Som oktaederet og ikosaederet er dette litt vanskeligere å forstille seg enn de andre, men ikke så vanskelig å bygge med plastbrikker eller pappbiter som har form som regulære femkanter.
Dodekaeder.
Dersom alle sideflatene er regulære sekskanter, ville summen av kantvinklene i hvert hjørne være minst 360º, siden kantvinkelen i en regulær sekskant er 120º. Derfor ville vi ikke få noe hjørne. Tilsvarende ville regulære mangekanter med mer enn seks kanter heller ikke kunne være sideflater i et regulært polyeder. Dermed er det bare de fem mulige hjørnekonfigurasjonene som vi har funnet. Faktisk er det også bare de fem platonske legemene som vi har beskrevet over.
Hvis vi teller opp antall sideflater, kanter og hjørner i hver av de platonske legemene får vi følgende tabell:
| tetraeder | oktaeder | heksaeder | dodekaeder | ikosaeder | |
| hjørner | 4 | 6 | 8 | 20 | 12 |
| kanter | 6 | 12 | 12 | 30 | 30 |
| sideflater | 4 | 8 | 6 | 12 | 20 |
Det er en fin øvelse å finne disse tallene når en har bygget de forskjellige legemene, og mange måter å komme fram på. Her skal jeg bare beskrive én måte. Når en kjenner
antall sideflater (noe må en telle) på et legeme, finner en antall kanter med å multiplisere
først med antall kanter på hver sideflate og deretter dele på antall sideflater som har en kant felles (altså to). Tilsvarende får en antall hjørner ved å multiplisere antall sideflater med antall hjørner på hver sideflate og deretter dele på antall sideflater inn i hvert hjørne.
Når en ser på tallene i tabellen for de platonske legemene er det mange av dem som er like. Tallene til oktaederet er de samme som for heksaederet eller terningen, bare i motsatt rekkefølge. Tilsvarende er det for dodekaederet og ikosaederet. Dette er selvsagt ikke helt tilfeldig. Midtpunktene på hver sideflate i en terning danner tilsammen hjørnepunktene i et oktaeder. Tilsvarende danner midtpunktene på hver sideflate i et oktaeder en terning.
Oktaederet og heksaederet er duale.
For hvert hjørne i terningen er det derfor en sideflate i oktaederet og omvendt. Med dodekaederet og ikosaederet er det på samme måte. Vi sier at heksaederet og oktaederet er duale polyedre, eller vi kunne si "søsken". Tilsvarende er heksaederet og oktaederet "søsken".
I tetraederet vil midtpunktet til sideflatene danne et nytt tetraeder, men dette står da opp ned i forhold til det opprinnelige. Tetraederet er derfor selvdualt, dual til seg selv eller "enebarn".
Descartes' formel
Summen av kantvinklene i hvert hjørne er mindre enn 360º. Forskjellen mellom 360º og denne summen kaller vi vinkelavviket. For et tetraeder er vinkelavviket i hvert hjørne 180º, mens i terningen er vinkelavviket 90º. Hvis vi summerer vinkelavviket i alle hjørnene i et tetraeder får vi 720º. Det samme får vi for terningen. Dersom vi regner etter, får vi det samme for alle de platonske legemene. Faktisk gjelder dette som en generell formel, oppdaget av Descartes:
I et konvekst polyeder er summen av vinkelavvikene i hvert hjørne lik 720º.
Dersom vi vet at alle hjørnene i et polyeder er like, kan vi ved å regne ut vinkelavviket i et hjørne bruke Descartes' formel til å finne antall hjørner totalt i polyederet. I et oktaeder er det fire trekanter inn i hvert hjørne. Derfor er vinkelavviket 120º i hvert hjørne. Siden hvert hjørne i oktaederet har vinkelavvik på 120º og summen av vinkleavvikene er 720º er det seks hjørner i oktaederet. I dodekaederet er summen av kantvinklene i et hjørne 324º siden kantvinkelen i en regulær femkant er 108º. Derfor er vinkelavviket i et hjørne 360º-324º=36º. I følge Descartes' formel må dermed dodekaederet ha 720º:36º=20 hjørner.
Eulers formel
Dersom en summerer antall hjørner og antall sideflater og trekker fra antall kanter i et
platonsk legeme får en alltid to. Dette gjelder også mer generelt for alle konvekse polyedere. Dette er et spesialtilfelle av Eulers formel som gjelder for alle polyedere. Den generelle formelen sier at
hjørner – kanter + sideflater =
der g betyr antall "hull" i polyedereret. En badering eller en smultring har ett hull. I et
polyeder som danner en badering ville Eulers formel gjelde med g=1, altså at antall hjørner pluss antall sideflater er lik antall kanter. For et polyeder som ser ut som en åttekantet badering gjelder formelen med g=2. Alle polyedre som kunne kle en ball, eller som kunne danne mønsteret på en ball, er konvekse. Da er det ingen "hull" og formelen gjelder med g=0. Et slikt mønster er selvsagt det som en finner på fotballer og håndballer. Det ligner på dodekaederet men er ikke helt det samme. Det er et såkalt avkortet ikosaeder, og vi skal se nærmere på dette og beslektede arkimediske legemer i neste avsnitt. For alle disse vil Eulers formel gjelde med g=0.
Arkimediske legemer
Der finnes selvsagt "uendelig" mange forskjellige polyedere. De platonske legemene er de mest perfekte, mens de arkimediske er på en måte de nest mest perfekte. Blant disse finnes fotballmønsteret. De arkimediske polyedrene er konvekse, og alle hjørnene er like, alle kantene er like og alle sideflatene er regulære mangekanter. Men de regulære mangekantene som danner sideflatene er ikke nødvendigvis like.
Hvis vi kutter eller korter av hjørnene i et ikosaeder, får vi en femkant i stedet for hvert hjørne siden det er fem sideflater inn i hvert hjørne i ikosaederet. Hver sideflate har fått avkortet sine tre hjørner, så de er blitt sekskanter. Hvis vi korter av riktig bit av hvert hjørne blir alle de nye femkantene og sekskantene regulære. Det polyederet vi da har fått kalles et avkortet ikosaeder og danner mønsteret på fotballen. Siden ikosaederet har 12 hjørner får vi 12 femkanter, og siden ikosaederet har 20 sideflater får vi 20 sekskanter. På mange fotballer er femkantene svarte, mens sekskantene er hvite.
Fotballmønsteret: et avkortet ikosaeder.
Det avkortete ikosaederet er et arkimedisk legeme. Ved å korte eller kutte av hjørnene på de andre platonske legemene får vi andre arkimediske legemer. Men det finnes også andre. Alle hjørnene skal være like, og alle skal være konvekse. For å undersøke hva som er mulig kan en se hvilke kombinasjoner av regulære mangekanter en kan sette sammen i et hjørne. Dette er en morsom oppgave med plastbrikker, prøv! Vi skal bare avsløre at i dette tilfelle er det ikke nok bare å se på kravet om at summen av kantvinklene i et hjørne skal være mindre enn 360º. For å si det på en annen måte er det ikke nok å se bare på hvordan hjørnene kan se ut hver for seg. For eksempel skal jo også Descartes' formel gjelde. Hvis vi for eksempel tenker oss et hjørne med to trekanter og en firkant, da er summen av kantvinklene 210º, så dette skulle være fullt ut mulig. Men vinkelavviket er 150º, som ikke går opp i 720º. Så for at Descartes' formel skal holde kan ikke et polyeder med to trekanter og en firkant i hvert hjørne ha et helt antall hjørner. Dette er selvsagt absurd, så det fins ikke noe slikt polyeder.
Del på Facebook