Bevis innen analytisk geometri

Fra boka "Solving Mathematical Problems", oversatt av Nils Voje Johansen

Mange geometriske oppgaver blir enklere å løse hvis man benytter andre deler av matematikken, slik som algebra og induksjon, for å løse dem. Denne oppgaven er et eksempel på nettopp det.

La oss starte med å gi uttrykket ”summen av kvadratene til elementene i L” et kortere navn, for eksempel X. Oppgaven vår er altså å regne ut X. Dette ser ut til å være en overkommelig oppgave; det er ikke en ”vis at”-oppgave eller en ”er det slik at”-oppgave, men en ren utregningsoppgave hvor vi for eksempel kan tenke på å benytte trigonometri og Pytagoras' setning. La oss se på et eksempel.

Når n = 4 har vi et kvadrat innskrevet i en enhetssirkel. De mulige lengdene som kan oppnås ved å forbinde to hjørner er kvadratets sidelengde lik $\sqrt{2}$ og diagonalens lengde lik 2. Fra dette finner vi ${X=\left(\sqrt{2}\right)}^2+2^2=2+4=6$. Tilsvarende får vi når n = 3 at den eneste lengden som opptrer er trekantens sidelengde, som er $\sqrt{3}$. Dermed blir $X={\left(\sqrt{3}\right)}^2=3$. Setter vi n = 5 blir situasjonen litt mer komplisert og vi trenger bøttevis av cosinus- og sinusregning for å finne svaret – så la oss vente litt med det. La oss i stedet se på n = 6. Sidelengdene i sekskanten blir lik sirkelens radius, altså 1. De korte diagonalene blir lik $\sqrt{3}$, mens de lange diagonalene (diameteren) blir lik 2. Fra dette finner vi $X=1^2+{\left(\sqrt{3}\right)}^2+2^2=8$. Til slutt ser vi på et underlig spesialtilfelle, nemlig n = 2. Da er ”polygonet” lik diameteren, og vi finner $X=2^2=4$. Vi samler resultatene fra disse eksemplene:

 

n	X
2?	4?
3	3
4	6
6	8

Vi har satt spørsmålstegn ved n = 2 siden det er litt spesielt å snakke om et polygon med kun to sider.

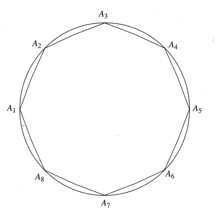
Denne lille tabellen gir oss imidlertid ikke mange tips om hvordan den generelle løsningen blir. Vi bør derfor se på et litt mer generelt tilfelle, og starter med å tegne en figur. Det er antagelig fornuftig å navnsette hjørnene, og da på en slik måte at det representerer en måte om kan brukes generelt. Vi starter med et hjørne og kaller det A₁ og fortsetter med solen med A₂, A₃, A₄, A₅ og opp til det siste hjørnet A_n, se figur 2.

 

Figur 2: Navnsetting av hjørnene.

Nå kan vi gjøre noen innledende observasjoner:

a) Det kan være av betydning om n er like eller odde. Hvis n er like vil den lengste diagonalen være lik diameteren. Vi legger også merke til at når n er like vil vi ha $\frac{n}{2}$ forskjellige varianter av linjestykker, mens når n er odde vil det være $\frac{(n-1)}{2}$ forskjellige.

b) Muligens vil X alltid være et heltall. I alle fall har det vært tilfelle med de eksemplene vi så på. Vi må imidlertid huske at spesialtilfellene vi behandlet, kvadratet, den likesidede trekanten og heksagonet, er spesielle og har ”kvadratrotaktige” lengdemål. Men tross alt gir det oss et håp om at svaret ikke vil være altfor stygt.

c) Oppgaven vår er å addere kvadrater av lengder, ikke lengdene selv. Det betyr at vi ikke lenger er innenfor ren geometri, men derimot har vi beveget oss over i analytisk geometri. Det impliserer at vi antagelig bør ta i bruk vektorer, koordinatgeometri eller kanskje komplekse tall? (I bunn og grunn vil imidlertid alle disse metodene være like.) Koordinatgeometri vil antagelig involvere mye grisete trigonometri, men vil forhåpentligvis sakte men sikkert føre oss mot målet. Vektorgeometri eller komplekse tall ser derfor noe mer lovende ut (med vektorregning kan vi benytte skalarprodukt, mens komplekse tall gir oss mulighet til å benytte komplekse eksponenter).

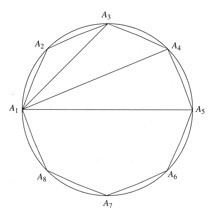
d) Det virker umulig å starte direkte på oppgaven siden vi ikke skal summere alle diagonaler, men bare dem med ulik lengde. Vi vil derfor først forsøke å omformulere spørsmålet slik at det lettere kan uttrykkes som en likning. (Likninger er trygg matematikk, ikke nødvendigvis så kreative og fulle av inspirasjon, men de er lette å manipulere. Generelt kan oppgaver uttrykkes ved hjelp av en eller annen likning – muligens med noen unntak innen kombinatorikk og grafteori.) Hvis vi begrenser oss til å se på diagonalene som løper ut fra ett enkelt hjørne av polygonet (fig. 3) vil vi finne alle de diagonalene vi trenger.

 

Figur 3: Diagonaler ut fra et enkelt hjørne.

Figur 3 viser et eksempel hvor n er like. Hvis vi begrenser oss til å se på øvre halvsirkel ser vi at alle ulike diagonaler vil forekomme én og bare én gang. Lengdene |A₁A₂|, |A₁A₃|, |A₁A₄| og |A₁A₅| vil utgjøre de lengdene vi er interessert i. Vi kan med andre ord uttrykke den ettersøkte størrelsen som:

X = |A₁A₂|² + |A₁A₃|² + |A₁A₄|² + |A₁A₅|²

Mer generelt kan vi si at vi er interessert i å beregne

X = |A₁A₂|² + ... + |A₁A_m|²

hvor $m=\frac{n}{2}+1$ (hvis n er like) og $m=\frac{n+1}{2}$ (hvis n er odde). Vi kan nå skrive opp problemet på en mer eksplisitt form:

La et regulært polygon med n hjørner være innskrevet i en enhetssirkel. La $m=\frac{n}{2}+1$ hvis n er like og $m=\frac{n+1}{2}$ hvis n er odde.
Beregn størrelsen X = |A₁A₂|² + ... + |A₁A_m|².

Det er litt uleilig at summen |A₁A₂|² + ... + |A₁A_m|² stopper ved A_m og ikke ved A_n som hadde vært mer naturlig. Vi kan rette på dette ved å se på den doble summen og deretter dele på 2. Vi benytter dessuten at symmetri gir at |A₁A_i|=|A₁A_n+2–i| og derfor:

X = $\frac{1}{2}$ (|A₁A₂|² + |A₁A₃|² + … + |A₁A_m|² + |A₁A_n|² + |A₁A_n–1|² + … + |A₁A_n+2–m|² ).

Her må vi huske på at når n er like har vi talt diagonalen |A₁A_{n/2 + 1}|² = 4 to ganger. Vi kan imidlertid rydde opp i dette ved å skille mellom like og odde tilfeller. For å få et penere og mer symmetrisk uttrykk kan vi dessuten fritt innføre leddet |A₁A₁|² siden det jo er lik 0. Gjør vi det finner vi:

X = $\frac{1}{2}$ (|A₁A₁|² + |A₁A₂|² + … + |A₁A_n|²)        (1)

når n er odde, og

X = $\frac{1}{2}$(|A₁A₁|² + |A₁A₂|² + … + |A₁A_n|²) + 2        (2)

når n er like (det ekstra 2-tallet kommer fra at i denne parentesen telles leddet med diagonalen, |A₁A_{n/2 + 1}|² = 4, bare en gang, og vi må derfor legge til $\frac{1}{2}\cdot 4=2$ for å ta vare på at den opprinnelig skulle vært talt med 2 ganger). Vi kan nå innføre størrelsen

Y = |A₁A₁|² + |A₁A₂|² + … + |A₁A_n|²        (3)

og regne ut Y i stedet for X. Fordelen med dette er

• så snart vi vet Y vil likning (1) og (2) gi oss X.
• Y er et penere uttrykk enn X, og derfor muligens lettere å beregne.
• for å regne ut Y trenger vi ikke å skille på like og odde verdier for n.

 

Hvis vi nå går tilbake til den lille tabellen vi laget for tilfellene n = 3, 4 og 6 kan vi nå i tillegg beregne Y (for eksempel ved likning (1) og (2)):

 

n	X	Y
2?	4?	4?
3	3	6
4	6	8
6	8	12

Fra verdiene på n og Y kan vi nå formulere en formodning om at Y = 2n. Fra likning (1) og (2) vil vi da se at X = n når n er odde og at X = n + 2 når n er like. Dette ser jo lovende ut, men vi må nå bevise at vår formodning er rett!

Vi tar i bruk vektorgeometri, siden det gir oss et kraftfullt verktøy til å manipulere uttrykk av den typen vi har i uttrykk (3). Siden kvadratet av lengden av en vektor v rett og slett er skalarproduktet av vektoren prikket med seg selv, v · v, kan vi skrive Y som

Y = (A₁ – A₁)·(A₁ – A₁) + (A₁ – A₂)·(A₁ – A₂) + … + (A₁ – A_n)·(A₁ – A_n).

Her betyr nå A₁, … , A_n vektorer og ikke punkter. Vi kan fritt velge origo i koordinatsystemet, men det naturligste er å la det være i sirkelsenteret. (Det nest mest naturlige er muligens å velge A₁ som origo.) En umiddelbar fordel ved å la origo ligge i sirkelsenteret er at alle vektorene A₁, … , A_n da vil ha lengde lik 1. Det betyr videre at A₁·A₁ = A₂·A₂ =… = A_n·A_n = 1. Hvis vi nå benytter dette til å regne ut skalarproduktene ovenfor ser vi generelt at

(A₁ – A_i)·(A₁ – A_i) = A₁·A₁ – 2A₁·A_i + A_i·A_i = 2 – 2A₁·A_i

Dette gir oss mulighet til forenkle uttrykket Y

Y = (2 – 2A₁·A₁) + (2 – 2A₁·A₂) + … + (2 – 2A₁·A_n)

Hvis vi samler like ledd og faktoriserer får vi

Y = 2n – 2 A₁·(A₁ + A₂ + … + A_n).

Vår formodning gikk ut på at Y = 2n. For å oppnå dette må vi vise at vektorsummen A₁ + A₂ + … + A_n er lik null. Dette gir seg selv ut fra symmetri (vektorene ligger symmetrisk og ”drar” like mye i alle retning, så nettokraften må bli null. Det lønner seg alltid å se etter muligheter for å utnytte symmetriegenskaper). Dermed har vi vist at Y = 2n, og dermed blir X = n når n er odde og X = n + 2 når n er like.