Bevis innen euklidsk geometri

Fra boka "Solving Mathematical Problems", oversatt av Nils Voje Johansen

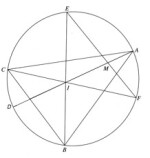
Figur 1: Sirkel med alle punktene i oppgaven markert.

Vi begynner selvsagt med å tegne en figur og markere alle punktene, se figur 1.

Jeg har i tillegg tatt meg den frihet å merke innsenterpunktet med I (halveringslinjene skjærer hverandre i innsenteret (sentrum i trekantens innskrevne sirkel), og punktet kan derfor være viktig). Jeg har også avmerket skjæringspunktet M mellom linjene AD og EF (som jo er stedet hvor vi ønsker å vise at linjene står vinkelrett på hverandre). Dermed kan vi skrive ned vårt studieobjekt som en likning, vi vil vise at $\angle AMF=90º$. (Vi kunne selvsagt formulert kravet ved hjelp av en av de andre vinklene der linjene skjærer hverandre, for eksempel $\angle IMF=90º$.)

Dette ser ut til å være en overkommelig oppgave: figuren er lett å tegne, og påstanden virker rimelig ut fra figuren. Stilt ovenfor et problem av denne typen vil ofte en direkte angrepsmåte fungere greit.

Vi skal beregne en vinkel i M. Ved første øyekast synes det ikke å være noe spesielt ved punktet M. Etter å ha satt inn alle de data vi har ser vi at vi kjenner mange vinkler, hovedsakelig på grunn av vinkelhalveringene, trekantene og den omskrevne sirkelen. Kanskje det vil kunne la seg gjøre å bestemme ∠AMF bare ved å finne nok andre vinkler? Tross alt er det jo mange læresetninger (teoremer) som bare venter på å bli brukt: summen av vinklene i en trekant er 180°, periferivinkler som spenner over samme sirkelbue er like store, vinkelhalveringslinjene i en trekant er konkurrente (skjærer hverandre i ett punkt).

Vi starter derfor med å navngi noen vinkler. Siden trekant ABC er utgangspunktet vårt og siden vi har halvert vinklene i trekanten, virker det fornuftig å starte med å navngi vinklene i trekanten:

$\alpha =\angle BAC$, $\beta =\angle ABC$ og $\gamma =\angle BCA$

(det er vanlig å betegne vinkler med greske bokstaver). Nå har vi selvsagt at $\alpha +\beta +\gamma =180º$. Vi kan lett finne en mengde andre vinkler fra dette, for eksempel er $\angle CAD=\frac{\alpha }{2}$. (Det beste er om du lager en tegning og setter på tilsvarende vinkler selv.) Vi kan nå benytte at vinkelsummen i en trekant er 180° og finne noen av de indre vinklene. For eksempel, siden I er innsenteret (skjæringspunktet mellom AD, BE og CF) i ABC, så kan vi lett finne at $\angle AIC=180º-\frac{\alpha }{2}-\frac{\gamma }{2}$ ved å se på trekanten AIC. Sannheten er at vi kan finne så godt som alle relevante vinkler – bortsett fra de ved M, som jo var de vi egentlig ønsket å finne. Vi må derfor forsøke å representere vinkelen ved M ved hjelp av andre vinkler som ikke er relatert til M. Heldigvis er dette ikke så vanskelig, vi kan for eksempel sette $\angle IMF$, som vi jo ønsker å vise at er 90°, lik
$\angle IMF=180º-\angle MIF-\angle IFM=180º-\angle AIF-\angle CFE$.
Dette bringer oss et langt steg fremover siden de to vinklene $\angle AIF$ og $\angle CFE$ er mye letter å bestemme. Vi finner

$\angle AIF=180º-\angle AIC=\frac{\alpha }{2}+\frac{\gamma }{2}$,
og fordi periferivinkler som spenner over samme sirkelbue er like store finner vi

$\angle CFE=\angle CBE=\frac{\beta }{2}$

Av dette får vi at

$\angle IMF=180º-\angle AIF-\angle CFE=180º-\frac{\alpha }{2}-\frac{\beta }{2}-\frac{\gamma }{2}=180º-\frac{180º}{2}=90º$,

akkurat det vi var på jakt etter.

Dette er en vakker måte å løse geometriske problemer på – rett og slett å arbeide seg frem til den ettersøkte vinkelen. Vinkler er vanligvis enklere å finne enn sidekanter (hvor du ofte må pløye deg gjennom stygge uttrykk med sinus og cosinus), og reglene er også lettere å huske.