Eksakte verdier

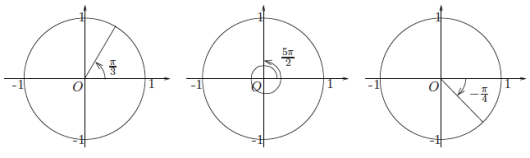
En enhetssirkel er rett og slett en sirkel av radius $1$ med sentrum i origo. Vi legger en vinkel $u$ inn i enhetssirkelen ved å plassere toppunktet i origo slik at det ene vinkelbeinet ligger langs $x -$ aksen, og slik at positive vinkler går mot klokka. På figuren under ser du vinklene

$u = \frac{π}{3} (60^{\circ}), u = \frac{5 π}{2} (450^{\circ}) og u = - \frac{π}{4} (- 45^{\circ})$

lagt inn i hver sin enhetssirkel.

Na kan vi definere de trigonometriske funksjonene for alle mulige vinkler:

definisjon. trigonometriske funksjoner

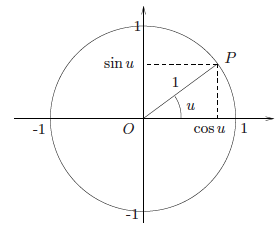
La $u$ være en vinkel målt i radianer, lagt inn i en enhetssirkel. La $P$ være skjæringspunktet mellom enhetssirkelen og det venstre vinkelbeinet til $u$ . Vi definerer funksjonene $\cos u$ , $\sin u$ og $\tan u$ ved at

$\cos u$ = førstekoordinaten til punktet $P$ ,

$\sin u$ = andrekoordinaten til punktet $P$ ,

$\tan u = \frac{\sin u}{\cos u}$ .

Funksjonene $\cos u$ og $\sin u$ er definert for alle $u \in ℝ$ . Funksjonen $\tan u$ er definert for alle $u \in ℝ$ bortsett fra de verdiene som gjør at $\cos u = 0$ , nemlig

$u = \frac{π}{2} + k \cdot π$ , $k \in ℤ$

For de aller fleste vinkler $u$ , må vi bruke kalkulator for å finne $\sin u$ , $\cos u$ og $\tan u$ (Tidligere brukte man svære tabeller!) Noen få vinkler kan vi imidlertid finne eksakte verdier for. De viktigste er sammenfattet i denne tabellen:

Current Time 0:00

Duration Time 0:00

Loaded: 0%

Progress: 0%

Stream TypeLIVE

Remaining Time -0:00

MatRIC: Eksakte verdier

Rettighetshaver: MatRIC ved Universitetet i Agder / MatRIC

Del på Facebook

Del på Facebook

Eksakte verdier

Lynkurs 11.-13.trinn

Trigonometri

Består av: