Addisjon av vektorer

For å forstå vektoraddisjon, kan det være greit å tenke vektorer som forflytning mellom punkter. Spiller det noen rolle hvilken vektor kommer først i summen?

Current Time 0:00

Duration Time 0:00

Loaded: 0%

Progress: 0%

Stream TypeLIVE

Remaining Time -0:00

MatRIC: Vektorregning

Rettighetshaver: Rettighetshaver: MatRIC ved Universitetet i Agder / MatRIC /

Addisjon av vektorene

$\vec{A B}$ og

$\vec{B C}$ betyr først å forflytte seg fra

$A$ til

$B$ , og så fra

$B$ til

$C$ . Summen blir den totale forflytningen fra

$A$ til

$C$ , altså vektoren

$\vec{A C}$ .

ADDISJON AV VEKTORER

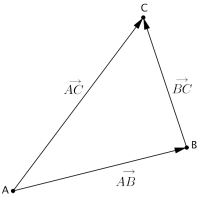
Addisjon av vektorene $\vec{A B}$ og $\vec{B C}$ :

$\vec{A B} + \vec{B C} = \vec{A C}$

ADDISJON AV VEKTORER PÅ KOORDINATFORM

La $\vec{u} = [x_{1}, y_{1}]$ og $\vec{v} = [x_{2}, y_{2}]$ være to vektorer. Vi adderer vektorer koordinatvis, det vil si

$\vec{u} + \vec{v} = [x_{1}, y_{1}] + [x_{2}, y_{2}] = [x_{1} + x_{2}, y_{1} + y_{2}] .$

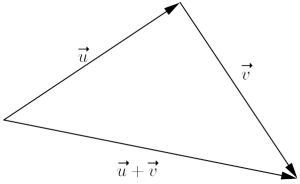
Vi har altså addert $x$ -verdiene og $y$ -verdiene hver for seg, og fått en ny vektor. Geometrisk tilsvarer dette å flytte $\vec{v}$ slik at den starter der $\vec{u}$ slutter, med samme retning og lengde som før vi flyttet den. Summen er nå pilen som starter der $\vec{u}$ starter og ender der $\vec{v}$ ender.

Vektoraddisjon kan tolkes som å først bevege seg langs den ene vektoren, så langs den andre vektoren.

Eksempel 1

Vi skal addere vektorene $\vec{u} = [1, 5] og \vec{v} = [11, 3]$ . Vi kan tenke at vi først beveger oss langs $\vec{u}$ , det vil si ett steg i $x$ -retningen og fem steg i $y$ -retningen. Så beveger vi oss langs $\vec{v}$ , elleve steg i $x$ -retningen og tre steg i $y$ -retningen. Den totale forflytningen blir dermed tolv steg i $x$ -retning og åtte steg i $y$ -retning, vektoren $[12, 8]$ . Vi kan kalle den nye vektoren for $\vec{w}$ og skriver

$\vec{w} = \vec{u} + \vec{v} = [1, 5] + [11, 3] = [12, 8]$

Eksempel 2

$[- 4, 2] + [1, 9] = [- 4 + 1, 2 + 9] = [- 3, 11]$

Vektoraddisjon er kommutativ

Leddenes rekkefølge spiller ingen rolle.

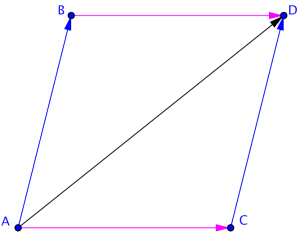
Det spiller ingen rolle hvilken vektor som kommer først i summen. Dette ser vi tydelig på figuren til høyre:

$\vec{A B} = \vec{C D} og \vec{A C} = \vec{B D}$ , likheter på grunn av lik lengde og retning.
Det er det samme om vi først forflytter oss langs $\vec{A C}$ og så langs $\vec{C D}$ , eller om vi først forflytter oss langs $\vec{A B}$ og så langs $\vec{B D}$ , summen av vektoren $\vec{A D}$ i begge tilfellene.

$\vec{A C} + \vec{B D} = \vec{B D} + \vec{A C} = \vec{A D}$

Addisjon av vektorer

Eksempel 1

Eksempel 2

Lynkurs 11.-13.trinn

Vektorer

Består av: