Kvadratsetningene
De tre kvadratsetningene er små huskeregler som gjør en matematikers hverdag litt enklere, og de er spesielt viktige når vi skal arbeide med andregradsuttrykk.
|
Teorem. Kvadratsetningene.
|
Bevis. Her er det ikke noe hokus-pokus. Det er bare å gange ut venstresidene, så får du høyresidene. For eksempel:
Noen lurer kanskje på hvorfor det er noe vits i å terpe så mye på disse tre «setningene» – det er jo likevel bare å regne ut hvis man skulle glemme dem. Det er selvfølgelig riktig, men de er såpass nyttige at det er lurt å huske dem utenat. Den beste måten å lære seg kvadratsetningene på er å regne en del eksempler. På denne og neste side skal vi se på noen.
Eksempel 1
Vi har
ved 1. kvadratsetning. Dette kan også skrives som
| . |
Vi har altså at
Når et uttrykk
Faktorisering av uttrykk
Med å faktorisere et uttrykk i x mener vi å skrive det som et produkt av lineære faktorer.
Eksempel:
Kvadratsetningene kan være til stor hjelp for å faktorisere kompliserte uttrykk. Generelt er det ingen metoder som forteller hvordan man kan faktorisere et vilkårlig uttrykk. Man er altså avhengig av ulike «triks», alt etter hva slags uttrykk det er snakk om. Ett slikt triks er å bruke kvadratsetningene motsatt vei– fra høyre mot venstre. Dette eksempelet viser oss hvor effektivt det kan være å gjøre dette.
Eksempel 2
Faktorisér uttrykket
Løsning. Kan man ikke kvadratsetningene, er det lett å stå fast her. Men etter å ha stirret en stund på uttrykket, kjenner vi igjen høyresiden i 1. kvadratsetning, med og . Og det betyr at vi kan skrive opp faktoriseringen direkte:
Del på Facebook
Begrep
-
Første kvadratsetning
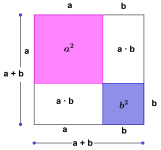
Første kvadratsetning sier at
.
-
Andre kvadratsetning
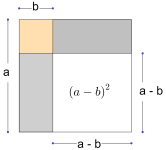
Andre kvadratsetning sier at
.
-
Konjugatsetningen
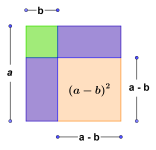
Konjugatsetningen kalles også tredje kvadratsetning:
.




