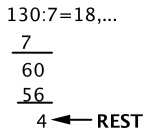Julekalender 2007, 5.-7. trinn
Lærerens instruksjoner
ALT DU FINNER PÅ DISSE NETTSIDENE KAN DU LASTE NED I ET UTSKRIFTSVENNLIG FORMAT (pdf), se vedlegget i høyrespalten.
Årets julekalender for 5.-7. trinn består av 12 enkeltstående oppgaver som kan løses uavhengig av hverandre.
Klasser som ønsker å delta i konkurransen om å vinne premier må sende inn løsningene i en e-post til 5-7trinn-jul2007@matematikk.org innen 11. januar.
Innholdet i e-posten må være:
Svar på oppgavene 1 til 12
Klasse(r):
Antall elever som har deltatt:
Kontaktpersons e-postadresse:
Skole:
Skolens postadresse:
Innsendingsfrist for konkurransen er 11. januar 2008.
Vinnerne offentliggjøres via startsiden, www.matematikk.org tirsdag 15. januar kl. 12.00.
Spørsmål kan sendes til post@matematikk.org.
Lykke til med oppgavene, og god jul!
Kommentarer/tips til noen av oppgavene:
Oppgave 1
Det er selvsagt flere måter å angripe dette problemet på, men en av dem kan være å starte med to farger og se om det er mulig å fargelegge de landene som har flest naboland. Hvordan går det med 3 farger? Hvordan går det med 4 farger?
Et annet tips er å bruke blyant og viskelær under utprøvingen, og markere fargene med bokstaver eller tall.
Oppgave 2
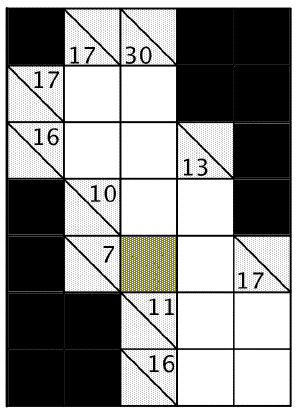
Kakurobrettet i oppgaveteksten kan byttes ut med følgende brett dersom noen av elevene trenger litt ekstra utfordring. Den markerte ruta i begge spillbrett gir samme tall.
Oppgave 3
Oppgaven bør brytes ned, og dere kan se på enklere versjoner først. Elevene trenger erfaringsmessig en del guiding for å få til denne oppgaven.
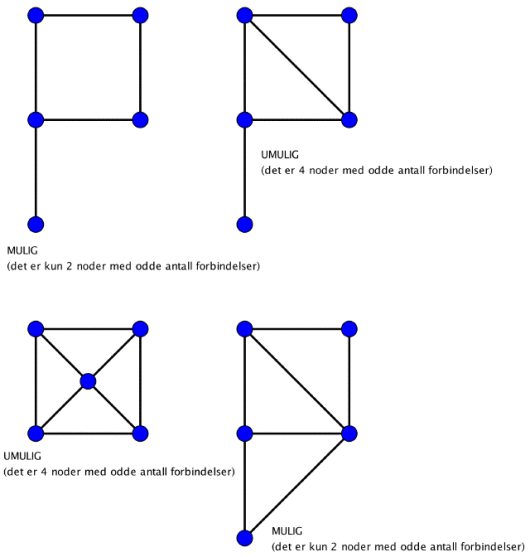
Vi kaller punktene for noder og strekene forbindelser mellom nodene (dere må gjerne finne deres egne ord dersom det passer bedre);
Hvilke er mulige og hvilke er umulige?
Start med å la elevene få prøve å finne ut hvilke som er mulige, og hvilke som er umulige.
Snakk om
- hva er likeheten mellom de to som er mulige
- hva er likheten mellom de to som er umulige
- tell forbindelser som går ut fra hver node, sjekk sammenheng
- oppsummer antall noder med odde forbindeleser og antall noder med partallsforbindelser
- hvor mange forbindelser det må være på en node dersom du skal kunne komme og gå derfra? (Det må være 2, 4, 6, ... et partalls antall forbindelser.)
- hvor mange forbindelser trenger vi på en node dersom vi skal begynne eller avslutte der? (Det må være 1, 3, 5, ... et oddetalls antall forbindelser.)
Euler viste at hvis det finnes flere enn to noder som har et odde antall forbindelser, så finnes det ingen løsning.
I tilfellet Königsbergs broer har alle fire nodene et odde antall forbindelser og derfor er det ikke mulig.
Oppgave 7
Det hele dreier seg om 4-gangen. Dersom du passer på å etterlate deg et antall som er delelig med 4 (altså 4, 8, 12) kan du alltid vinne. Når vi starter med 15 fyrstikker må første trekk være å ta vekk 3, slik at du kommer ned til 12, så gjør vi følgende
- hvis motspilleren tar bort 1 fyrstikk, tar du bort 3
- hvis motspilleren tar bort 2, tar du bort 2
- hvis motspilleren tar bort 3, tar du bort 1
Vanligvis vet vi ikke hvor mange fyrstikker som ligger i bunken til å begynne med, så da er det om å gjøre å telle når det nærmer seg slutten - etterlat deg alltid et antall som hører med til 4-gangen og du er garantert seier!
Oppgave 8
Vi synes figuren ser ut som en lama, men det er ikke poenget med oppgaven og vi kommer til å godta alt fra katt til giraff.
Oppgave 10
Vi har ikke gjort som Cæsar! Vi har valgt å flytte et annet antall plasser enn 3. Vi har gjort slik at Z blir til A.
Oppgave 11
I denne oppgaven har vi valgt å bruke ordene diagonalt, vertikalt og horisontalt, og dersom en velger å la disse stå bør en være sikker på at elevene kan/skjønner betydningen.
Oppgaven kan også løses ved at elevene selv er spillbrikker. Da er det lurt å la eleven som plasseres i øverste høyre hjørne få på seg f.eks en refleksvest e.l. slik at det blir lettere å holde oversikten. Rutenettet kan f.eks krittes opp i skolegården, eller det kan lages med tape i gymsal eller klasserom.
En utvidelse av oppgaven kan være å spørre om det er mulig å forutsi hvor få trekk som trengs i et 6x6 rutenett. Tips til fremgangsmåte er å starte med 2x2, utvide til 3x3 og se på 4x4 kan vi finne et mønster i utvidelsene? Må/bør vi undersøke 5x5, eller ser vi et mønster som vi kan bruke?
Minste antall trekk for 6x6 er 32 - det utvides med 7 trekk for hver gang.
NB!
Start skal alltid ligge i øverste høyre hjørne.
Mål er alltid i nederste venstre hjørne.
Den ledige ruta skal alltid være nederst til høyre.
Oppgave 12
Her er det viktig med en introduksjon hva betyr det å se noe fra sør, øst, vest eller nord?
Det må også være klart hvordan nord, sør, øst og vest ligger i forhold til hverandre.
I denne oppgaven er det ikke ett tall som er svaret, men et intervall. Hva er minste mulige antall klosser og hva er største mulige antall klosser?
I gjennomføring av denne oppgaven kommer det litt an på hvor god tid dere har til rådighet. Med god tid er det fint å la elevene selv få oppdage at det kan være ulikt antall klosser, ellers kan det opplyses med en gang at det er et minimumsantall (som er 6) og et maksimumsantall (som er 20).
Jobb gjerne i grupper.
Elevens oppgaveark
KART OG FARGEPROBLEMER
Matematikere lurer på mye rart, og en av disse litt underlige tingene de har lurt på er hvor få farger de egentlig trenger for å fargelegge et kart dersom de landene som ligger rett ved siden av hverandre (naboland) ikke skal ha lik farge. Naboland er de landene som har felles grense.
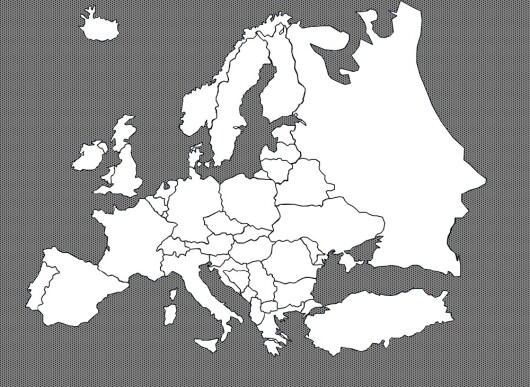
Oppgave 1:
Hvor få farger trenger dere for å fargelegge Europas land slik at ingen naboland har lik farge?
NB! Kartet er ikke helt korrekt, det er utelatt en rekke små land som blant annet Liechtenstein,Vatikanet og Kypros. I tillegg er ikke hele det skraverte området sjø/hav.
KAKURO
Våren 2005 kom det japanske spillet Sudoku til Norge og bredte seg som en farsot, hakk i hæl kom Kakuro.
Kakuro er faktisk ikke opprinnelig fra Japan. Spillet oppsto i USA og het "Cross Sums". Cross Sums sto på trykk første gang i et amerikansk kryssordhefte en gang på 1960-tallet.
Den japanske forretningsmannen, McKee Kaji kom i 1980 over tallpuslespillene under en reise til USA. Han oppdaget hvilke muligheter spillet hadde, tok det med hjem til Japan og omformet det.
Kaji kaldte spillet for Kasan Kurosu, som er en kombinasjon av det japanske ordet for "å legge sammen" og uttalen av det engelske ordet "cross". Kakuro er en sammentrekning av Kasan Kurosu.
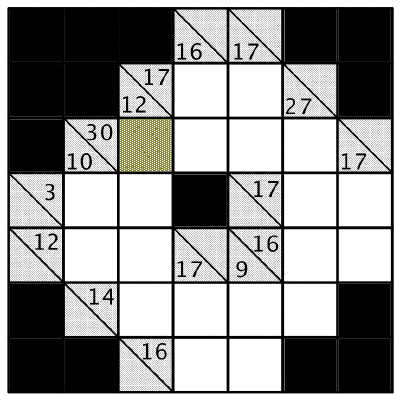
Oppgave 2: Hvilket tall må stå i den markerte ruta?
Kakuro er altså et matematisk kryssord hvor det gjelder å kunne legge sammen tall. Reglene for spillet er slik:
- Plassér to eller flere av sifrene 1, 2, 3, 4, 5, 6, 7, 8, eller 9 slik at de sammenlagt gir summen (tallet) som står oppgitt over eller til venstre for en tallrekke.
- Et siffer kan ikke brukes mer enn én gang i hver sum.
Oppgave 2
Hvilket tall må stå i den markerte ruta?
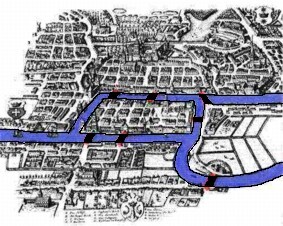
Broene i Königsberg
Oversiktskart over Königsberg med elva og de 7 broene.
Byen Königsberg ble grunnlagt på 1200-tallet av Den tyske orden og ligger ved Østersjøen mellom dagens Litauen og Polen. Königsberg ble russisk i 1945 og heter i dag Kaliningrad etter Sovjetunionens statsoverhode under Den andre verdenskrig.
Elven Pregel (dagens Pregolja) rant gjennom Königsberg og forgrenet seg slik at den lagde ei øy i byen. Syv broer gikk over elven som vist på dette bildet:
Innbyggerne i Königsberg gikk mange turer over broene, og det berømte problemet var om det var mulig å gå en tur gjennom byen der man krysset hver av de syv broene nøyaktig en gang. Det var matematikeren Leonhard Euler (1707-1783) som løste dette i 1736
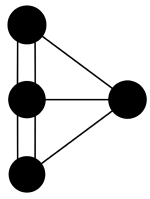
Oppgave 3:
Forenklet kart over broene i byen Königsberg.
Hva fant Euler ut er det mulig, eller er det umulig?
Vi har forenklet kartet over broene i Königsberg i figuren under, og nå lurer vi på er det mulig å føre en blyant fra punkt til punkt i figuren uten å tegne på noen av strekene mer enn én gang?
Svar JA, eller NEI på oppgaven.
Finn feilene!
Anne og Per fikk igjen matematikkbøkene sine fra læreren.
Anne: Æsj, jeg fikk feil på oppgave 3.
Per: Hæ, det gjorde jeg også!
De blar opp i bøkene og finner ut at de ikke har gjort den samme feilen.
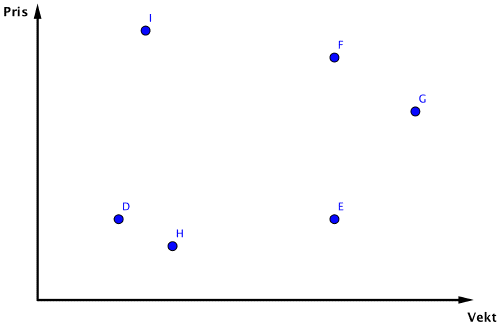
Her er oppgaven Anne og Per har svart på:
Hvert punkt i diagrammet står for en pose godteri.
a) Hvilke poser har samme vekt?
b) Hvilke poser koster like mye?
c) Hvilken av posene H eller E er det mest lønnsomt å kjøpe?
Anne har svart:
a) H og I har samme vekt.
b) D og E koster like mye.
c) E er mest lønnsom.
Per har svart:
a) E og F har samme vekt.
b) E og F har samme pris.
c) H er mest lønnsom.
Oppgave 4:
Hvem av dem har rett på deloppgave a), b) og c)?
Vet du hvilken fødselsdag du har?
Du vet så klart hvilken fødselsdato du har, men vet du hvilken ukedag du ble født på? Det finnes matematiske oppskrifter for å finne fødselsdagen og andre dager også. En en av disse oppskriftene er laget av matematikeren Carl Friedrich Gauss (1777-1855).
En ting dere må vite for å kunne bruke oppskriften, er om dere er født i et skuddår eller ikke (gjelder bare for dem som er født i januar eller februar). I denne oppgaven er oppskriften tilpasset årene fra 1900 til 1999.
Vi viser oppskriften til Gauss gjennom et eksempel: Hvilken ukedag var 10. mai 1995?
Oppskrift:
| Ta de to siste sifrene i årstallet (merk at 2007 blir 107) | 1995 | 95 |
| + legg til av de to siste sifrene uten å ta med desimaler | 95:4=23,75 | 23 |
| + legg til fødselsdatoen | 10. mai | 10 |
| + legg til |
1 for januar (0 i skuddår) |
2 |
| = legg sammen alle tallene | 130 |
Del summen på 7 og resten i divisjonen vil gi deg ukedagen.
Med 4 som rest finner vi ut fra tabellen under at 10. mai 1995 var en onsdag.
| Rest fra divisjon | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Ukedag | lørdag | søndag | mandag | tirsdag | onsdag | torsdag | fredag |
Oppgave 5:
Kong Harald er født 21. februar 1937 - hvilken ukedag var dette?
PROBLEMLØSING
Når vi for eksempel skal utføre et delestykke, følger vi en oppskrift som sier oss hvordan vi skal gå frem for å komme fram til svaret. Oppskriften består i et bestemt antall mellomregninger som skal gjøres før vi kommer til svaret. Denne oppskriften kalles i matematikken for en algoritme. Når vi ikke kjenner til, eller har lært, algoritmen blir oppgaven et problem, og da må vi til med problemløsing.
I problemløsing er det om å gjøre å finne en (din egen) måte å løse oppgaven på, og det kan være mange forskjellige måter som fører fram til samme løsning. Noen kan løse et problem ved å regne, andre ved å tegne.
Uansett om du bruker algoritmer eller holder på med problemløsing i matematikk er det viktig at du går tilbake og kontrollerer om svaret ditt er sannsynlig i forhold til oppgaven. Du bør også huske på at det noen ganger tar lang tid å komme fram til et svar!
Oppgaven i dag kan løses på flere måter, lykke til.
Oppgave 6:
Per Olsen hadde en bondegård, og på den gården hadde han både kalkuner og griser.
På dyrskuen i Seljord i høst hadde Olsen med seg alle dyrene sine. På dyrskuen fikk han solgt 10 griser og 40 kalkuner. De dyrene Olsen reiste hjem igjen til gården sin med hadde til sammen 100 bein og 30 hoder.
Hvor mange kalkuner hadde Olsen med seg til Seljord?
SPILL OG VINNERSTRATEGI
De fleste av oss synes det er gøy å vinne i spill. I noen spill er det mulig å lage en plan eller strategi for hvordan man må gå fram for å vinne finne en vinnerstrategi. De av dere som har spillt Tre på rad vet kanskje hvordan vinnerstrategien er? Dersom én av spillerne kjenner vinnerstrategien, vil denne spilleren alltid vinne. Dersom begge kjenner strategien blir det mye verre...
NIM er et fyrstikkspill hvor det er mulig å finne en vinnerstrategi.
Spillet foregår på denne måten;
- to spillere veksler på å ta 1, 2 eller 3 fyrstikker fra en bunke som ligger på bordet
- den som tar den siste fyrstikken har vunnet
Det spiller egentlig ingen rolle hvor mange fyrstikker som ligger i bunken på bordet, men la oss si det ligger nøyaktig 15 fyrstikker der - hvordan er vinnerstrategien?
Oppgave 7:
Beskriv vinnerstrategien i NIM med de reglene vi har gitt i teksten over.
KOORDINATSYSTEM
René Descartes (1596-1650) var en fransk filosof og matematiker. Han er kjent for å ha uttalt "Cogito, ergo sum" (som er latin og betyr "Jeg tenker, derfor er jeg."), og å finne opp koordinatsystemet vi bruker den dag i dag. I skolen sier vi bare koordinatsystem, men vi kunne også sagt det kartesiske koordinatsystem, for aksene i et vanlig koordinatsystem er oppkalt etter Descartes.
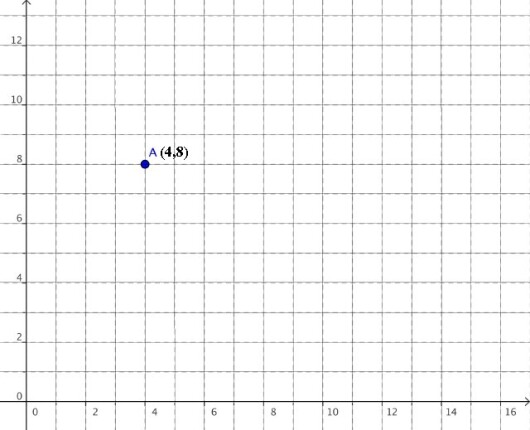
Descartes hadde bruk for å angi punkters posisjon når han tegnet geometriske figurer. Akkurat som du kan slå opp i kartbøker å finne ut at Stasjonsveien ligger i rute G5, ville Descartes si f.eks hvor hjørnet A i firkanten er i forhold til de andre hjørnene. Han fant ut at han måtte ha noe å referere til når han skulle angi posisjon, og til dette brukte han en x-akse (eller førsteakse) og en y-akse (eller andreakse) som han satte vinkelrett på hverandre. Så bestemte han at et sett koordinater (x,y) skulle leses på følgende måte: gå først langs x-aksen, så langs y-aksen for å finne punktet.
Punktet A i figuren har koordinater (4,8). Dette betyr at vi først har gått 4 langs x-aksen og så 8 langs (parallelt med) y-aksen.
Oppgave 8:
Tegn et kartesisk koordinatsystem med med lik skalering på begge koordinataksene og trekk en rett linje fra
(4,8) til (3,9)
(3,9) til (2,8)
(6,3) til (10,3)
(10,3) til (12,1)
(12,1) til (12,9)
(10,6) til (10,10)
(10,10) til (13,10)
(13,10) til (14,9)
(12,9) til (14,9)
(4,8) til (4,6)
(4,6) til (10,6)
(6,3) til (4,1)
(4,6) til (4,1)
Hva slags figur blir dette?
"Det er jo logisk!"
Har dere hørt noen si dette? Hva mener de egentlig, hva er logikk?
Om du slår opp i en ordbok på ordet logikk finner du
logikk (fra gresk, av logos 'ord, tanke, fornuft')
1 læren om lover, prinsipper for følgeriktig tenkning; tenkelære studere
l- / filosofisk, matematisk l- / formal l- del av logikken som gjør bruk av spesielle symbolspråk
2 (evne til) klar, følgeriktig tankegang; regelbundet sammenheng
det er en brist i l-en / hvor er l-en? / naturens indre l-
Å kunne tenke logisk hjelper deg i matematikken, det å kunne gjenkjenne riktige argumentasjoner er viktig både når du skal lese matematikk og formulere argumenter på egenhånd.
I dagens oppgave kreves det at du klarer å holde hodet kaldt, at du sorterer og rydder opp i problemet at du tenker logisk.
Oppgave 9:
Jørgen, Hans, Stine og Marte er fire venner som bor i samme gate. De har
hvert sitt forskjellige kjæledyr, og om du spør dem om hvilket fag de
liker best på skolen får du fire forskjellige svar.
De fire vennene er noen luringer og spør du hvem av dem som eier apen får
du disse opplysningene:
- han som liker naturfag har ikke katt som kjæledyr
- Stine har ikke hund og liker ikke norsk
- Jørgen liker heller ikke norsk
- Marte synes gym er det beste faget, men tåler ikke katter
- han som ikke liker naturfag har en katt som kæledyr
- hamsteren bor hos den som liker naturfag
- det er ei av jentene som er glad i matematikk
Hvem eier apen?
KRYPTOGRAFI
Har du noen hemmeligheter? Kanskje er det noen du vil dele dem med? Kanskje noen som er langt borte, så du må sende den som brev eller tekstmelding? Hva om noen andre åpner brevet, eller leser tekstmeldinga? Hvis dette er noe du gjerne vil unngå, bør du lære deg litt om kryptografi, eller hemmelig skrift. Kryptografi kan gjøre deg istand til å skrive ned meldinger på en slik måte at bare de du ønsker kan lese dem.
I dag skal vi se på en kodeteknikk som selveste Julius Cæsar har gitt navnet til - Cæsarkoder. Da Cæsar ønsket å sende viktige meldinger til sine offiserer ute i felten krypterte han dem (altså kodet dem) ved å flytte alle bokstavene i alfabetet tre plasser til høyre. På denne måten ville meldingen "Angrip ved daggry" bli "Dqjuls yhg gdjjuøf", idet en "A" blir til en "D", en "B" blir til en "E", , en Æ blir til en A, en Ø bli til en B osv. Når offiserene - som kjente til Cæsars system - fikk den krypterte meldingen, dekrypterte de den ved å flytte bokstavene tre plasser til venstre.
Oppgave 10:
Vi har gjort som Cæsar og laget en kryptert melding. Men, vi har flyttet et annet antall plasser enn 3!
OER HY PIWI HIXXI ?
Hva er den hemmelige meldingen?
How low can you go?
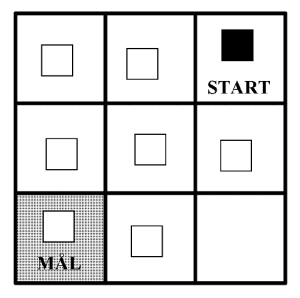
Tegn opp et 3x3 rutenett og legg ut 8 spillbrikker som i figuren. Her kan du bruke hva som helst, men det er lurt at én av brikkene er lett gjenkjennelig.
Det er om å gjøre å få den brikken som ligger i øverste høyre hjørne, på START, ned til MÅL på færrest mulig trekk.
REGLER
- en brikke kan bare flyttes til en ledig rute
- en brikke kan bare flyttes én rute om gangen
- en brikke kan aldri flyttes diagonalt, bare horisontalt og vertikalt
Oppgave 11:
Hva er minste antall trekk fra start til mål?
Norske byggeklosser
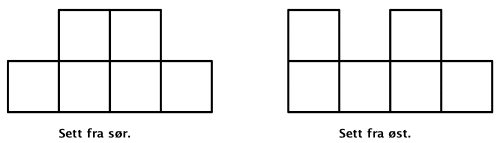
Tenk dere at vi bygger med kuber (centikuber, terninger e.l.). Etter en liten stund har vi satt opp de kubene vi kan se i figurene under.
Oppgave 12:
Hvor mange kuber har vi brukt?