Øvingsoppgaver med fasit

Silje har sparepenger på en konto. Funksjonen $K\left(t\right)=8500\cdot {1,019}^t$ beskriver hvor mye penger det er på denne kontoen etter t år.

a) Hvor mye penger satte Silje inn?

b) Hvor stor er renten?

Funksjonen f gitt ved

$f\left(x\right)=125x^2-1550x+25000$
der x skal være mellom 0 og 10.

a) Finn $f^{\prime }\left(5\right)$.
b) Hvilken x - verdi gir minst f(x)?

c) Hva er definisjons- og verdimengden i denne problemstillingen?

På 1990 - tallet var det 38 100 innbyggere i en by. Antallet innbyggere økte med 1 % hvert år etter 1990. Hvor mange innbyggere var det i byen i 1990? Hvor mange innbyggere er det i byen etter t år?

Eli har en årslønn på 360000 kr. Vi antar at hun de x neste årene har en gjennomsnittlig lønnsvekst på 3,5 % per år.

a) Sett opp en funksjon for lønna til Eli om x år.

b) Hva er årslønna hennes om 5 år?

c) Når passerer hun 500000 kr i årslønn?

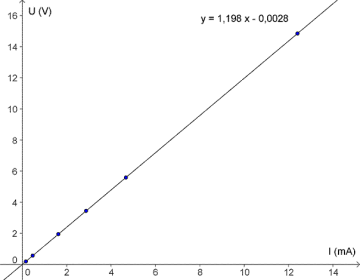
I et fysikk-forsøk skal sammenhengen mellom strømmen $I$ gjennom og spenningen $U$ over en motstand $R$ bestemmes. Måleresultatene er gitt i tabellen under.

a) Tegn inn punktene i et koordinatsystem med $I$ langs førsteaksen og $U$ langs andreaksen. Tilpass ei rett linje til punktene ved lineær regresjon på lommeregneren. Hva er likningen til linja?

b) Argumenter for at sammenhengen mellom strømmen gjennom og spenningen over motstanden er gitt ved Ohms lov:

    $U=R\cdot I$

Hva var verdien av $R$ i dette forsøket (gi svaret i $k\mathrm{\Omega }=\frac{V}{mA}$)?

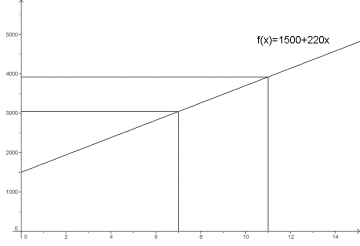
Anders selger abonnementer på et tidsskrift. Han har 1500 kr i grunnlønn per uke. I tillegg kommer 220 kr per solgte årsabonnement.

a) Sett opp en funksjon $f\left(x\right)$ som viser Anders' ukelønn når han selger $x$ abonnementer på en uke.

b) Tegn grafen til $f\left(x\right)$ for $x$ mellom $\mathrm{}$0 og 15.

c) Vis grafisk og ved regning hva Anders tjener hvis han selger 7 abonnementer på 1 uke.

d) Vis grafisk og ved regning hvor mange abonnementer han har solgt hvis han tjener 3920 kr på en uke.

BMI-verdien b til en person er gitt ved formelen:

$b=\frac{v}{h^2}$

der v er vekten i kilogram og h høyden i meter.

a) Finn en formel for vekten v uttrykt ved høyden h og BMI-verdi b.

b) Bruk formelen til å finne vekten til en person som er 183 cm høy når BMI-verdien er 25.

Aslaug satte inn 1000 kr på en høyrentekonto. Renten er 10% per år Hvor mye penger har Aslaug etter 3 måneder?

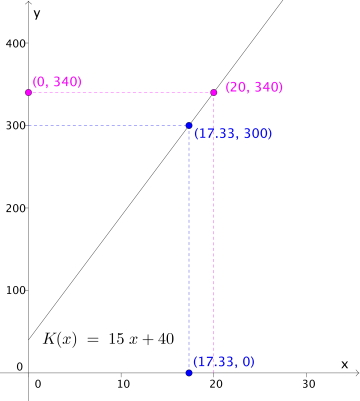
Karl Magnus setter seg i en taxi og taksameteret viser 40 kroner. Under turen ser han at det med jevne mellomrom automatisk legges til et beløp på taksameteret. Han spør sjåføren hva dette er og får vite at det er kilometerprisen og at den ligger på 15 kr. Karl Magnus mener at drosjeutgiftene K etter x km kan skrives som $K=15x+40$. Stemmer dette? Tegn grafen til K når x er mellom 0 og 30. Løs grafisk hva en drosjetur på 20 km koster og finn ut hvor langt Karl Magnus kan kjøre drosje for 300 kr.

Tabellen viser høyden (i meter) til et tre er etter t år:

0 - 2,00

1- 2,40

2 - 2,88

3 - 3,46

4 - 4,15

5 - 4,98

6 - 5,97

Plott dette som punkter i et koordinatsystem. Finn et funksjonsuttrykk som viser hvor høyt treet er etter t år. Endrer funksjonsuttrykket seg hvis treet er 1,0 meter høyt ved år 0?