Øvingsoppgaver med fasit
Lenke til dette oppgavesettet (kan bokmerkes)Oppgaver
1
Regn ut den gjennomsnittlige veksthastigheten for funksjonen når x er fra 2 til 2,01 og fra 2 til .
2
Sarah deriverer funksjonen på følgende måte:
Rett opp feilene i Sarahs derivasjon.
3
Deriver funksjonen:
4
Finn når funksjonen f er gitt ved
5
Deriver . Deriver den deriverte.
6
Hvor mange ganger kan du derivere en polynomfunksjon? Begrunn svaret.
7
Hva betyr uttrykket "derivere hvert ledd for seg"?
8
9
En elev skal finne den deriverte til i og gjør følgende:
Hvilken feil ble gjort? Hva er det riktige svaret?
10
Fasit
1
12,03 og
2
3
4
5
Den derivertes deriverte
6
7
8
9
6
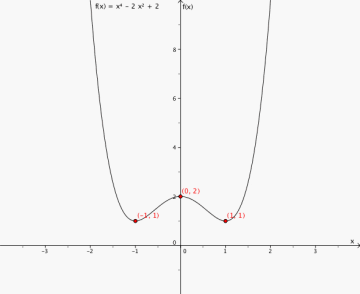
10
toppunkt (0,2)
bunnpunkter (-1,1) og (1,1)
Grafen synker når x<-1 og når 0