Øvingsoppgaver med fasit
Lenke til dette oppgavesettet (kan bokmerkes)Oppgaver
1
Det er alltid to skjæringspunkter mellom en rett linje og en andregradsfunksjon. Er denne påstanden riktig? Begrunn svaret.
2
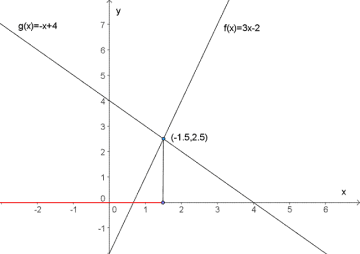
Bruk et digitalt hjelpemiddel til å tegne grafene til og . Finn skjæringspunkt.
3
Vi har gitt funksjonene og .
a) Løs ulikheten grafisk på lommeregneren.
b) Løs ulikheten ved regning.
4
Bestem a og b slik at funksjonene
har uendelig mange skjæringspunkter.
5
Tegn grafen til funksjonen nedenfor på lommeregneren i det oppgitte området. Bestem x-verdiene til alle skjæringspunkter i med x-aksen.
6
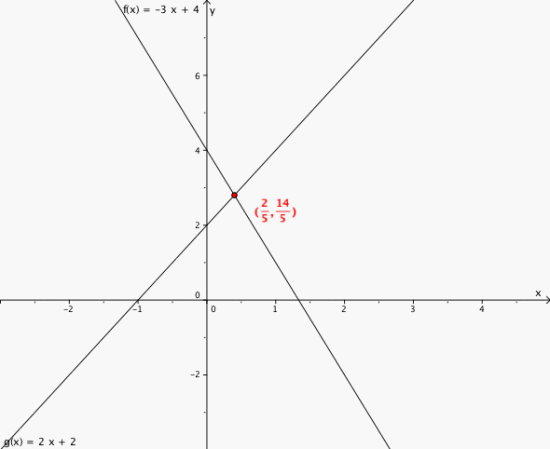
Finn skjæringspunkt mellom
ved regning og ved å tegne linjene i samme koordinatsystem.
7
Tegn grafene til f og g i samme koordinatsystem. Vi har gitt at og . Løs ligningen både grafisk og algebraisk.
8
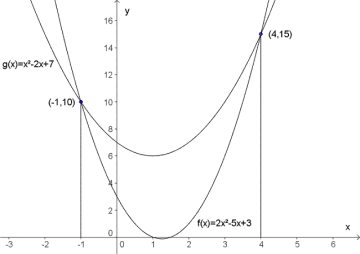
Vi har gitt funksjonene og .
a) Tegn grafene i samme koordinatsystem.
b) Løs grafisk og ved regning hvor grafene skjærer hverandre.
9
Finn skjæringspunktet til
10
Å finne løsningene for et likningssystem er det samme som å uttrykke likningene som funksjonene og finne skjæringspunktene mellom grafene. Er denne påstanden riktig? Begrunn svaret.
Fasit
1
Nei, et moteksempel er
2
3
a) og b)
4
5
x = -1, x = 1
6
(5, -2)
7
8
a) og b)
b)
9
10
Ja.