Øvingsoppgaver med fasit
Lenke til dette oppgavesettet (kan bokmerkes)Oppgaver
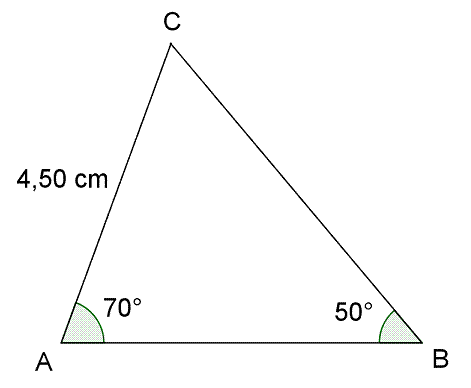
1
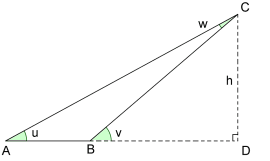
a) Finn høyden fra C ned på AB.
b) Finn BC og AB.
c) Finn arealet av trekanten.
2
a) En dag er solhøyden 32o. Et tårn kaster en 48 m lang skygge. Hvor høyt er tårnet?
b) Utenfor tårnet står en 8 m høy flaggstang. Hvor lang skygge kaster flaggstanga?
c) En annen dag kaster tårnet en skygge på 35 m og 75 cm. Hvor lang skygge kaster flaggstanga nå?
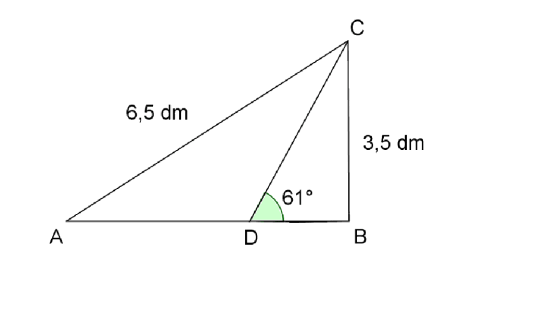
3
. Finn lengden av , og .
4
a) På en flyplass står to instrumenter i hver sin ende av en rullebane. Rullebanens lengde er kjent. Instrumentene måler vinkelen siktelinja mot et fly danner med bakken. Forklar hvordan denne informasjonen kan brukes til å bestemme flyets høyde.
b) To personer står rett overfor hverandre, men de er på hver sin side av et tårn. De ser begge mot spiret på toppen. Siktelinja til den ene personen danner en vinkel på med bakken, mens siktelinja til den andre personen danner en vinkel på med bakken. Personene står m fra hverandre. Hvor høyt er tårnet?
5
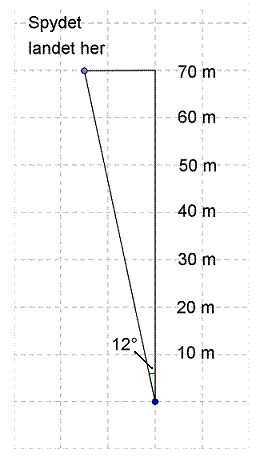
En spydkaster kaster et spyd slik at det danner en vinkel på 12o med aksen til tilløpet. Spydet når akkurat 70 meters-merket på denne aksen, se figuren. Hvor langt er spydkastet?
6
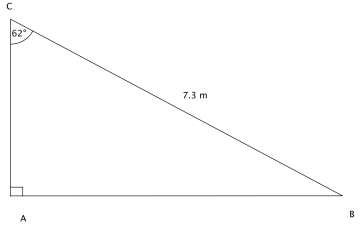
7
er rettvinklet med .
a) Hvor lange er sidene og hvis og m?
b) Hvor lange er sidene og hvis og dm?
8
9
Reis opp tommelen mens du holder armen strak ut foran deg. Se på tommelen først med det ene øyet, så med det andre. Legg merke til at tommelens plassering skiftes i forhold til bakgrunnen.
En tilsvarende effekt kan brukes for å måle avstanden til våre nærmeste stjerner. Avstanden mellom punkter i jordens bane rundt sola på forskjellige tider av året, svarer da til avstanden mellom øynene i eksemplet over. En nær stjerne fotograferes flere ganger gjennom et år, og det kartlegges hvordan stjernen tilsynelatende beveger seg i forhold til de fjernere bakgrunnsstjernene.
Vinkelen på figuren kalles parallaksen til den nære stjernen, og denne kan måles av astronomene. For vår nabostjerne Proxima Centauri er . Middelavstanden mellom jorda og sola er m og lysår m.
a) Hva blir avstanden til Proxima Centauri i lysår?
b) Undersøk på lommeregneren hvor stor forskjellen er mellom og . Hva er grunnen til at det blir slik?
10
Finn hypotenusen når motstående katet er 12 cm og vinkelen er 45o
Fasit
1
a) h = 4,23 cm
b) BC = 5,52 cm og AB = 5,09 cm
c) 10,8 cm2
2
a) 30,0 m
b) 12,8 m
c) 9,53 m
3
dm, dm og dm
4
a) På figuren befinner instrumentene seg i punktene og . Flyet er i punkt . Siktelinjene danner vinklene og med bakken. Vi ser at vinkelen . Videre gir sinussetningen . Til slutt får vi, siden er rettvinklet, at .
b) m.
5
71,56 m
6
7
a) m og m
b) dm og dm
8
9
a) lysår
b) For svært små vinkler er hypotenus og lengste katet nesten like lange. Forholdet mellom korteste katet og hypotenus (sinus) blir da omtrent likt forholdet mellom korteste katet og lengste katet (tangens). Evt. ser man at siden når .
10
17.0 cm