Øvingsoppgaver med fasit
Lenke til dette oppgavesettet (kan bokmerkes)Oppgaver
1
La være funksjonen gitt ved .
a) Vis at avstanden fra origo til grafen til er gitt ved .
b) Finn den minste avstanden grafisk på lommeregneren.
2
Under et forsøk der man undersøkte avkastingen av korn som funksjon av mengden av hvete, kom forskere frem til funksjonen der g(h) er avkastingen av korn i tusener og h er mengden av hveten i kg. Hvor stor er den største avkastingen?
3
Bestem ved hjelp av digitalt verktøy, toppunktet på grafen f :
4
Hva forteller toppunktet til en funksjon deg?
5
Hva forteller et bunnpunkt til en funksjon deg?
6
Tegn grafen på lommeregneren og finn koordinatene til eventuelle topp- og bunnpunkter for disse funksjonene:
7
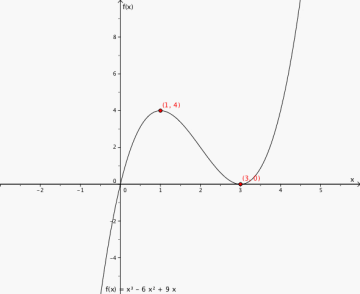
a) Finn toppunktene og bunnpunktene til f.
b) Finn monotoniegenskapene til f.
c) Tegn grafen til f.
8
Arealet av et rektangulært området er gitt som . Hva er det største arealet området kan ha?
9
Funksjonen f er gitt ved
a) Finn
b) Løs ligningen og tolk svaret
10
Fasit
1
a) Hint: Pytagoras' setning
b)
2
4,8 millioner kilogram
3
( - 2, - 2 )
4
5
6
Toppunkt: (-0,33, 1,19)
Bunnpunkt: (1, 0)
7
a) Toppunkt (1,4). Bunnpunkt (3,0)
b) Grafen vokser når x<1 og når x>3. Grafen minker når 1
8
1250
9
a)
b)