Øvingsoppgaver med fasit

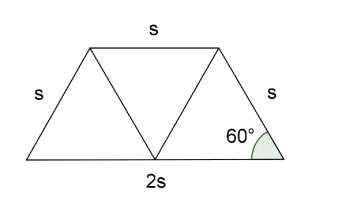
Tre likesidete trekanter med sidelengde $s$ settes sammen til å danne et trapes.

a) Tegn trapeset og vis at omkretsen blir $5s$.

b) Bruk én av trekantene til å vise at $\sin \left({60}^o\right)=\frac{\sqrt{s^2-\frac{s^2}{4}}}{s}=\frac{\sqrt{3}}{2}$.

c) Vis at arealet av trapeset er $A=\frac{3\sqrt{3}}{4}{s}^2$.

Løs eksponentiallikningene ved regning:

a) $4^x=9$

b) $8^{x-2}=15$

c) ${1,4}^{2x}=139$

I 1900 bodde det 5,14 millioner i Sverige. I år 2000 var det 8,86 millioner. Hvor mange bodde i Sverige i 1718 hvis vi sier at økningen har vært eksponentiell?

Løs likningen $2\cdot 3^x=17$.

Koboltisotopen ${}^{60}Co$ har en halveringstid på 5,3 år, mens cesiumisotopen ${}^{137}Cs$ har en halveringstid på 30 år. Anta at du ved tiden $t=0$ har $M\left(0\right)=12$ gram ${}^{60}Co$ og $m\left(0\right)=5$ gram ${}^{137}Cs$.

a) Forklar hvorfor mengden ${}^{60}Co$ etter $t$ år er gitt ved $M\left(t\right)=M\left(0\right)\cdot {\left(\frac{1}{2}\right)}^{t/5,3}$, mens mengden ${}^{137}Cs$ er gitt ved $m\left(t\right)=m\left(0\right)\cdot {\left(\frac{1}{2}\right)}^{t/30}$.

b) Etter hvor lang tid har du igjen 5 gram ${}^{60}Co$ ? Hvor mye ${}^{137}Cs$ har du igjen da?

c) Når er det igjen like store mengder av de to isotopene? Vis at eksakt svar blir $t=\frac{1}{(\frac{1}{5,3}-\frac{1}{30})}\cdot \left(\frac{\lg \left(\frac{5}{12}\right)}{\lg \left(\frac{1}{2}\right)}\right)$.

Eli har en årslønn på 360000 kr. Vi antar at hun de x neste årene har en gjennomsnittlig lønnsvekst på 3,5 % per år.

a) Sett opp en funksjon for lønna til Eli om x år.

b) Hva er årslønna hennes om 5 år?

c) Når passerer hun 500000 kr i årslønn?

Daniel setter 10 000 kr i banken og får 5% rente per år. Etter x år er beløpet gitt ved formelen

$y=10000\cdot {1.05}^x$

 Christian setter samtidig inn 12 000 kr i en annen bank, men han får bare 2% rente per år. Etter x år er beløpet hans gitt ved formelen:

$y=12000\cdot {1.02}^x$

Når har de like mye penger i banken? Hvor mye penger har de da?

Du setter 25000 kr på konto med 2% rente.

a) Hvor mye har du i banken etter 10 år hvis renta er stabil, og du ikke rører pengene?

b) Finn ved regning når du har 28000 kr på konto.

Løs ligningen:

$1000\cdot {1.07}^x=1200$

Løs likningen $2\cdot {1,025}^x=3\cdot {1,015}^x$. Vis utregning.