Øvingsoppgaver med fasit

Vi trekker et kort fra en vanlig kortstokk med 52 kort. Regn ut sannsynligheten for følgende begivenheter:

a) Kortet er en kløver 2
b) Kortet er en ruter
c) Kortet er et ess
d) Kortet er ikke et billedkort

27 elever fra en skole skal på tur til Nederland. Av dem har 12 elever tysk og 15 elever har fransk. Fem av elevene har både tysk og fransk. En elev trekkes ut tilfeldig for å være reiseleder. Hva er sannsynligheten for at reiselederen

a) har tysk
b) har tysk eller fransk eller begge deler
c) verken har tysk eller fransk

En skole har 3 klasser. I klasse 1 er det 21 elever hvorav 9 er jenter, i klasse 2 er det 17 elever hvorav 4 er jenter og i klasse 3 er det 28 elever hvorav 16 er jenter. Rektoren ved skolen skal tilfeldig plukke ut en elev.

Vi ser på hendelsene

• "elev er jente" = J
• "elev går i klasse 1" = EN 

a) Tegn opp et venndiagram for utfallet som er delt i 3 (en del for hver klasse). Så deler du hver av disse 3 delene i 2 og angir antall jenter og antall gutter for hver av klassen.

b) Hva er sannsynligheten for P(J) ?

c) Hva er sannsynligheten for P(EN)?

d) Hva er sannsynligheten for P(J|EN)?

e) Hva er sannsynligheten for P(EN|J)?

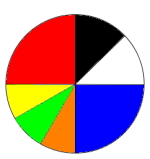
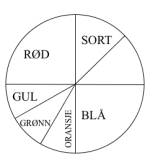
Dette er samme lykkehjulet, men de uten fargeskriver kan bruke tegningen til høyre der fargene er erstattet med fargens navn.

Figuren viser et lykkehjul. Du snurrer lykkehjulet rundet én gang og ser hvilken farge det stopper på. Skriv opp en sannsynlighetsmodell for for forsøket. Hva er sannsynligheten for at lykkehjulet stopper på gul, rød eller oransje?

Til eksamen fikk 3 av 5 elever beste karakter.
Hva er sannsynligheten for at en tilfeldig valgt elev ikke fikk beste karakter?

I en bøtte ligger det 8 baller. En ball trekkes tilfeldig ut av bøtta. Utfallsrommet er U = {rød ball, blå ball, grønn ball, svart ball} og

   P(rød ball) = $\frac{1}{4}$ , P(blå ball) =  $\frac{3}{8}$, P(svart ball) = $\frac{1}{8}$

 a) Bestem P(grønn ball)

 b) Hvor mange røde baller, grønne baller, blå baller og svarte baller må legges hvis vi ønsker en uniform sannsynlighetsmodell?

I en gruppe på 70 personer er det 42 med blondt hår, 34 som ikke har blå øyne og 23 som har blondt hår men ikke blå øyne. 
Hvis en person med blå øyne trekkes tilfeldig ut fra gruppa, hva er sannsynligheten for at denne personen har blondt hår?

I en skuff ligger det 6 blå, 2 grå og 8 svarte sokker. Du tar to sokker i mørket, først en og så en til. Hva er sannsynligheten for at du får

 a) to blå sokker

 b) to grå sokker

 c) to svarte sokker

 d) to sokker med samme farge

En mattelærer ga klassen sin to tester. 25% av elevene i klassen besto begge testene og 42% av elevene besto bare den 1. testen. 
Hvor mange av de som besto den 1. testen besto også den 2. testen? 

I en spørreundersøkelse ble 348 personer spurt om de feirer Santhans. 152 av de spurte svarte ja. Hvor stor sannsynlighet for ja-svar kan vi sette opp etter dette?