Øvingsoppgaver med fasit

I denne oppgaven skal vi regne ut de ukjente vinklene i trekanten. Avgjør på forhånd om vi får to sett løsninger. Det kan være lurt å tegne hjelpefigur.
$a=12.1cm,b=7.7cm,\angle B={31.4}^o$

a = 12,1 cm, b = 7,7 cm, $\angle$B = 31,4°

Finn den minste vinkelen i en trekant med sidelengder 35,6 cm, 58,43 cm og 52,23 cm.

To sider i en trekant er 4.7 cm og 5.2 cm. Den mellomliggende vinkelen er 42.3^o. Hvor lang er den tredje siden?

En mann skal svømme over ei elv, men elva er hele $4,8$ km bred, og han er ikke sikker på om han klarer å svømme hele strekket i ett. Omtrent midt i elva, $2,1$ km fra der mannen skal hoppe uti (og det er bare ett sted langs bredden det egner seg å hoppe uti), er det ei øy. Men dersom han skal svømme til øya, må han svømme ${24}^o$ til høyre for den korteste veien over elva.  Hvor mye lengre må han svømme hvis han skal få lagt inn ei hvilepause på øya?

I trekanten ABC er AB = 3.4 cm, BC = 5.2 cm og AC = 7.3 cm. Regn ut vinklene i denne trekanten.

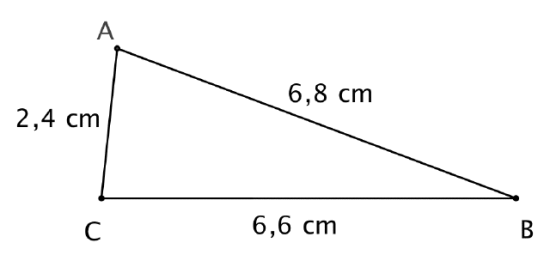
Finn $\angle$C, rund av til nærmeste hele gradtall.

I trekant ABC er a = 12, c = 15 og vinkel B = 75^o. Finn lengden av b.

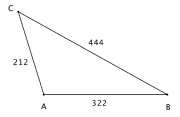
Bruk trekanten til høyre og bestem vinkel C.

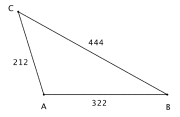
Bruk trekanten til høyre og bestem $\angle$A.

En landmåler står i et punkt $P$ og måler $\angle RPQ={39,7}^o$. I tillegg måles avstandene $PQ=312$ m og $PR=170$ m. Hva er avstanden mellom punktene $Q$ og $R$ ?