Augustin-Louis Cauchy

Augustin-Louis Cauchy
Cauchy var en meget betydningsfull matematiker på begynnelsen av 1800-tallet. Cauchy kritiserte infinitesimalregningen som ble innført av Newton og Leibniz. Han kom frem til den moderne definisjonen av kontinuitet, basert på grensebegrepet.
Augustin-Louis Cauchy ble født i 1789, året for den store franske revolusjonen. Selv om han var av borgerlig herkomst, følte han seg hele livet knyttet til den aristokratiske samfunnsordenen som gikk under med revolusjonen. Faren var en innflytelsesrik administrator som til tross for sitt rojalistiske grunnsyn fortsatte å stige i gradene under de omskiftelige regimene.
Cauchy var utdannet ved den nye École Polytechnique og fikk der den beste ingeniørutdanningen som ble gitt i Frankrike. Mens han arbeidet som ingeniør ved et stort havneprosjekt i Cherbourg, begynte han å sende matematiske artikler til vitenskapsakademiet i Paris. Han ble fort lagt merke til, og i 1815 fikk han en stilling ved École Polytechnique. En av hans oppgaver var å forelese integral- og differensialregning for ingeniørstudentene, og siden han var misfornøyd med de vanlige lærebøkene, utarbeidet han sine egne fremstillinger som ble publisert i 1821 og 1823. Cauchy forkastet de tradisjonelle infinitesimalene, som ble innført av Newton og Leibniz, og baserte isteden fremstillingen på grensebegrepet. Han kom frem til den moderne definisjonen av kontinuitet, og han var den første som beviste middelverdisetningen og forstod dens betydning.
Cauchys fremstilling var et revolusjonerende fremskritt som viste hvordan man ved hjelp av grensebegrepet kunne unngå de logiske problemene som infinitesimalene ledet til. Pedagogisk var den imidlertid ingen suksess studentene klaget, og skolens administrasjon påla Cauchy å vende tilbake til den tradisjonelle undervisningsmetoden. Men for matematikere rundt om i verden kom Cauchys fremstilling til å danne skole.
Politisk og religiøst var Cauchy like reaksjonær som han var revolusjonær i matematikken. Etter Napoleons fall gikk makten i Frankrike tilbake til Bourbonfamilien, og i årene som fulgte ble det gjort utallige forsøk på å vende tilbake til tiden før revolusjonen. Ludvig XVIII (1815-1824) hadde virkelighetssans nok til å bremse utviklingen, men under hans bror, Karl X (1824-1830), fikk de konservative kreftene fritt spillerom. Cauchy støttet denne utviklingen helhjertet, og da Karl X ble styrtet under juli-revolusjonen i 1830, nektet Cauchy å avlegge troskapsed til den nye kongen og forlot Frankrike. Han skulle ikke vende tilbake før i 1838.
De første årene i eksil levde Cauchy i Torino, men i 1833 flyttet han til Praha for å være privatlærer for hertugen av Bordeaux. Den 14 år gamle hertugen var ikke bare barnebarn av Karl X, men også Bourbonfamiliens nye tronpretendent. Valget av lærer var katastrofalt Cauchy hadde aldri ry på seg for å være noen stor pedagog, og hans forsøk på å holde disiplin ble effektivt kneblet av hans overdrevne respekt for elevens kongelige status.
Da hertugen av Bordeaux avsluttet sin utdannelse i 1838, hadde han fått varig avsmak for matematikk, og Cauchy hadde kastet bort noen av sine beste år på en oppgave han ikke hadde forutsetninger for å løse. Under sitt opphold i Praha hadde Cauchy forøvrig et kort møte med matematikeren Bolzano, men dette møtet ser ut til å ha blitt like resultatløst som Cauchys lærergjerning.
Da Cauchy vendte tilbake til Paris i 1838, hadde han mistet sitt professorat ved École Polytechnique, men var fortsatt medlem av vitenskapsakademiet. I årene som fulgte prøvde han på forskjellig vis å skaffe seg en ny stilling, men det var først etter februar-revolusjonen i 1848 at han igjen fikk en ledende posisjon ved et universitet. Han fortsatte å arbeide aktivt med matematikk helt til sin død i 1857.
Cauchy var en sammensatt person, full av motsetninger. Som matematiker er han en av tidenes største og mest produktive arbeidet med analysens grunnlag utgjør bare en liten del av hans innsats. Hans arbeider innenfor teorien om komplekse funksjoner og for sine fundamentale bidrag til kontinuumsmekanikken er godt kjent. Like idérik og fantasifull som han var som matematiker, like trangsynt og dogmatisk var han i andre spørsmål.
Han oppfattet utvilsomt seg selv som en mann med høye idealer og strenge prinsipper, men i sin omgang med andre var han ofte smålig og skjødesløs, og mange vitenskapelige oppdagelser gikk tapt eller ble forsinket fordi Cauchy rotet bort manuskriptene eller utnyttet dem til egen fordel.
Del på Facebook
Begrep
-
Analyse
Den matematiske analyse studerer ulike fenomeners forandringsprosesser eller dynamikk, og gjør blant annet bruk av grenseverdi og kontinuitet. Eksempler på deler av analysen er funksjoner av en eller flere reelle variabler, funksjoner av komplekse variabler og trigonometriske rekker.
-
Funksjon
En funksjon er en sammenheng mellom to eller flere størrelser. En funksjon tilordner til hvert element i en mengde (definisjonsmengden) ett element i en annen mengde (verdimengden).
Eksempel: For funksjonen , vil alltid gi
-
Grenseverdi
En uendelig tallfølge a1, a2, a3, ...har grenseverdi A dersom vi kan få an så nær A vi vil ved å velge n stor nok.
-
Infinitesimal
En "uendelig" liten størrelse. Et viktig begrep i matematisk analyse. Brukes for eksempel til definisjon av og regning med differensialer og integraler.
-
Integralregning
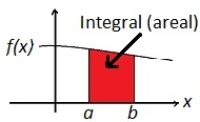
Integralregning er forbundet med arealbegrepet. Et areal kan uttrykkes ved et bestemt integral, og det kan beregnes ved integrasjon. Integralet fra a til b av funksjonen f kan tolkes som arealet av det området som begrenses av funksjonens graf, x-aksen og de vertikale linjene x=a og x=b.
-
Kontinuitet
Brukes om en funksjon dersom grafen er sammenhengende. Gis i matematisk analyse en mer presis definisjon.
-
Kontinuum
Den ordnede mengden av de reelle tallene.
-
Middelverdisetningen
En setning om reelle funksjoner som sier at for enhver korde til grafen til en kontinuerlig og deriverbar funksjon fins det en tangent i et punkt mellom endepunktene som er parallell med korden.








