Topp- og bunnpunkter
Ofte er vi interessert i når en funksjon har sin maksimale verdi eller sin minimale verdi. Dette skjer i topp- og bunnpunktene til funksjonen.
La funksjonen være prisen til en vare som varierer med tiden . Vi ønsker å kjøpe varen når den er billigst, altså når prisen er lavest. Dette er bunnpunktet til . For å tjene mest på varen, ønsker vi å selge denne når prisen er høyest eller når toppunktet nås.
Et toppunkt for en funksjon er et punkt i definisjonsmengden der funksjonsverdien er større enn i alle nabopunkter, altså alle punkter i et intervall rundt .
Et bunnpunkt for en funksjon er et punkt der funksjonsverdien er mindre enn i alle nabopunktene, altså alle punktene i et intervall rundt . Ekstremalpunkter er en fellesbetegnelse på topp- og bunnpunkter til en funksjon.
Vi skiller mellom lokale og globale ekstremalpunkter. Et globalt toppunkt er et punkt der funksjonsverdien er høyere enn alle andre funksjonsverdier av på hele definisjonsområdet. Et lokalt toppunkt er, som navnet indikerer, en topp lokalt på grafen. Det betyr at hvis du ser på bare en del (som inneholder punktet), så har punktet høyere funksjonsverdi enn alle andre funksjonsverdier i den delen.
Tilsvarende gjelder lokale og globale bunnpunkter.
Definisjon. Lokale og globale ekstremalpunkter
- har et lokalt maksimum i dersom for alle verdier av i nærheten av .
- har et globalt maksimum i dersom for alle verdier av i hele definisjonsområdet.
- har et lokalt minimum i dersom for alle verdier av i nærheten av .
- har et globalt minimum i dersom for alle verdier av i hele definisjonsområdet.
En samlebetegnelse på maksimums- og minimumspunkter er ekstremalpunkter.
Dersom er et ekstremalpunkt kaller vi verdien for den korresponderende ekstremalverdien.
Begrepene toppunkt og bunnpunkt brukes også ofte: Hvis har et (lokalt) maksimum i , har grafen et (lokalt) toppunkt i , og tilsvarende med bunnpunkt.
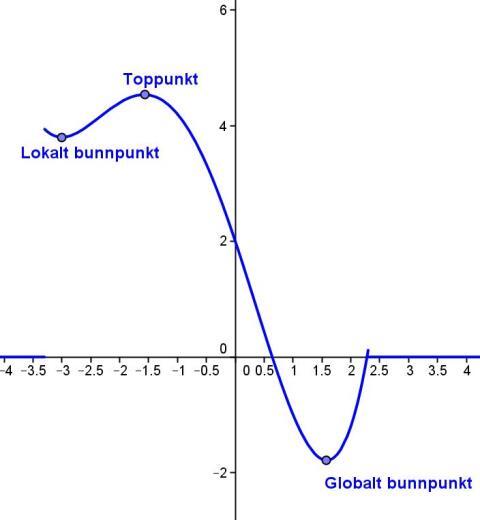
Figur 1 under illustrerer forskjellen mellom lokale og globale ekstremalpunkter. Legg merke til at alle globale ekstremalpunkter også er lokale.
I praksis bruker vi sjelden definisjonen over når vi skal regne ut ekstremalpunktene til en funksjon. I stedet drar vi nytte av det vi gjorde i forrige seksjon. Der så vi nemlig at grafen til var voksende i intervaller der , og avtagende i intervaller der . Dette betyr at i punkter der skifter fortegn, flater grafen ut og gir enten et topp- eller bunnpunkt. Mer presist:
Teorem
Anta at er kontinuerlig og deriverbar i , og at .
- Dersom skifter fortegn fra + til − i , har et lokalt maksimumspunkt i .
- Dersom skifter fortegn fra − til + i , har et lokalt minimumspunkt i .
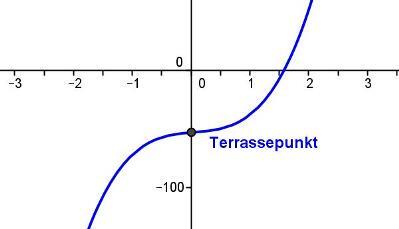
Dersom og ikke skifter fortegn i , har vi det vi kaller et terrassepunkt. Topp-, bunn- og terrassepunkter er altså de eneste punktene på en graf der tangenten kan være horisontal (se figuren under).
Eksempel
Oppgave. Bestem de lokale maksimums- og minimumspunktene til funksjonen og undersøk om noen av dem er globale.
Løsning.
Vi finner først den deriverte:
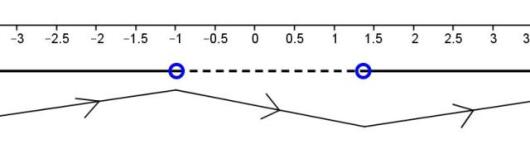
Fortegnslinjen ser slik ut:
Den forteller at er positiv fram til , og negativ etter. Punktet er derfor et lokalt maksimumspunkt. Tilsvarende har vi et lokalt minimumspunkt når . Ingen av disse er imidlertid globale, fordi går mot uendelig når , og mot minus uendelig når .
Del på Facebook