Øvingsoppgaver med fasit
Lenke til dette oppgavesettet (kan bokmerkes)Oppgaver
1
Løs likningssettet
.
2
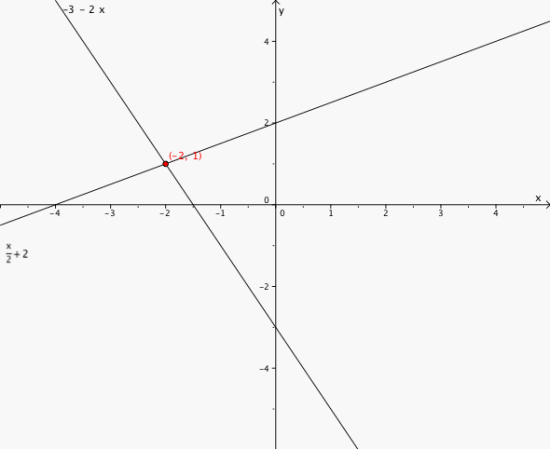
Løs ligningssettet grafisk:
3
To lineære funksjoner med samme stigningstall vil alltid ha et skjæringspunkt. Er denne påstanden riktig? Begrunn svaret.
4
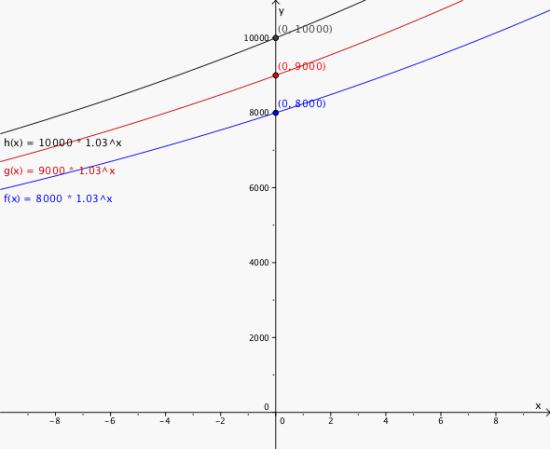
Eksponentialfunksjonene f, g og h er gitt ved:
a) Tegn grafene til f, g og h i samme koordinatysstem.
b) Finn skjæringspunktet med andreaksen for hver av grafene ovenfor. Hva oppdager du? Forklar.
5
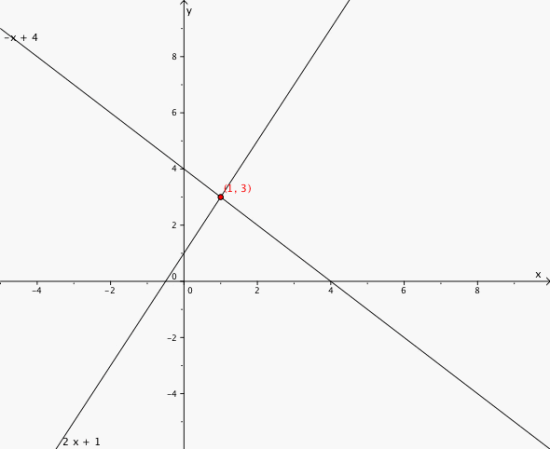
Løs ligningssystemet grafisk:
6
Løs likningssettet
7
Løs likningssettet grafisk
.
8
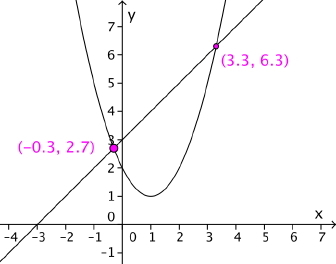
En funksjon er gitt ved .
a) Vis at punktene og ligger på grafen til .
b) Hva er stigningstallet til sekanten gjennom og ?
c) Sekanten gjennom og skjærer grafen til også i et tredje punkt. Finn koordinatene til dette grafisk på lommeregneren.
d) Vis at .
e) Finn nullpunktene til .
9
Løs ligningssettet grafisk og ved hjelp av lommeregneren:
10
Bestem a og b slik at funksjonene
har uendelig mange skjæringspunkter.
Fasit
1
Skjæringspunktet er .
2
x = -2 og y = 1
3
Nei, at to lineære funksjoner har samme stigningstall betyr at de er parallelle, og så lenge det er to ulike funksjoner, er konstantleddet forskjellig og dermed har funksjonene ingen skjæringspunkt.
4
a)
b)
5
To løsninger:
6
Skjæringspunktet er .
7
Linjene er parallelle og derfor skjærer ikke hverandre.
8
b)
c)
e)
9
x = 1 og y = 3
10