Øvingsoppgaver med fasit
Lenke til dette oppgavesettet (kan bokmerkes)Oppgaver
1
Bestem ved regning for hvilke verdier av ulikheten
ikke har noen løsning. Tolk deretter svaret grafisk.
2
Undersøk om funksjonen har topp- eller bunnpunkt. Oppgi koordinatene til punktet.
3
Funksjonen er gitt ved .
a) Finn
b) Når er funksjonen h(x) størst?
4
5
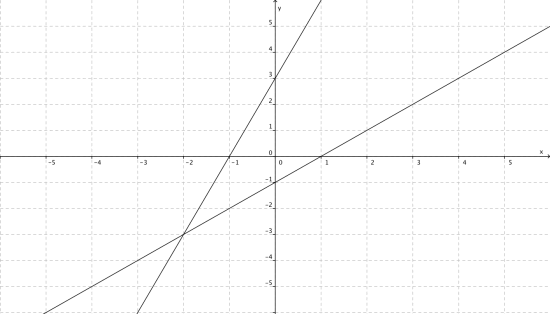
Bruk grafene til å finne løsningen til likningssettet
6
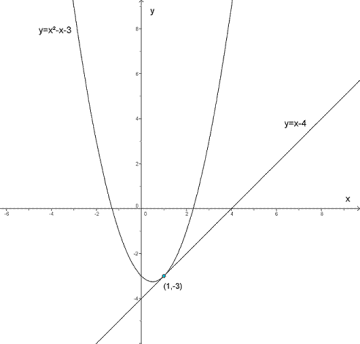
Finn skjæringspunkt for
7
Undersøk om funksjonen har topp- eller bunnpunkt. Oppgi koordinatene til punktet.
8
f(x)
9
Bestem a og b slik at funksjonene
har uendelig mange skjæringspunkter.
10
En sylinder har overflaten m2, og radius i grunnflaten.
a) Vis at høyden i meter er gitt ved .
b) Vis at volumet til sylinderen er gitt ved .
c) Finn det maksimale volumet sylinderen kan ha.
Fasit
1
2
Dette er en rett linje uten topp- eller bunnpunkt.
3
a)
b)
4
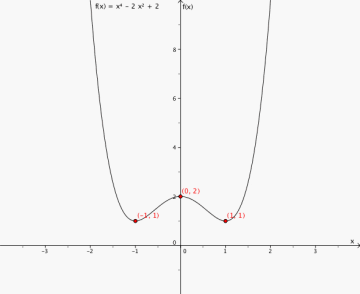
toppunkt (0,2)
bunnpunkter (-1,1) og (1,1)
Grafen synker når x<-1 og når 0
5
Skjæringspunktet er .
6
Skjæringspunktet er (3,4).
7
Funksjonen har et toppunkt i (0, -1).
8
9
10
c) m3