Øvingsoppgaver med fasit

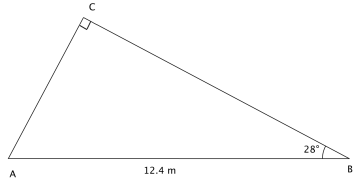
Regn ut

a) Lengden av kateten BC.
b) Lengden av kateten AC.
c) Arealet av trekanten.

I $\mathrm{\Delta }ABC$ er $AB=12 \mathrm{cm}, AC=13 \mathrm{cm} \mathrm{og}$ $\angle B={90}^o$. Vi feller ned en normal fra $B$ til hypotenusen $AC$. Hvor langt er det fra $A$ til fotpunktet $D$ for normalen?

En regulær sekskant har sider som er 4 cm lange.

a) Regn ut vinkelen ved hvert hjørne.

b) Fra hvert hjørne går det tre diagonaler. Regn ut lengdene av disse.

En regulær sekskant har sidekanter på 1 cm. Hvor stort er arealet av sekskanten?

I en rettvinklet trekant er katetene 8 cm og 15 cm. Regn ut arealet av trekanten, og finn høyden på hypotenusen.

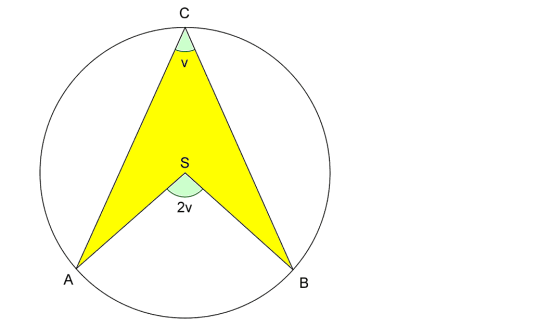
Periferivinkelen ( $$$v$ ) er alltid halvparten så stor som sentrumsvinkelen ($2v$ ).  Vi lar $AC=BC$.

a) Vis at dersom $v={90}^o$, er arealet av det fargede området $T=r^2$, der $r$ er radius i sirkelen.

b) Vis at arealet av sirkelen utenom det fargede området for en generell vinkel $v$ er gitt ved $A=\pi r^2-T=(\pi -\sin v)r^2$. Du kan få bruk for at $\sin ({180}^o-v)=\sin v$ (husk at for to supplementvinkler $u$ og $v$, er $\sin u=\sin v$ ).

I $\mathrm{\Delta }$ABC er AB = 44,3 cm, AC = 28,6 cm og $\angle$B = 23,3°. $\angle$C kan ha to forskjellige verdier. Finn arealet av trekanten for hver verdi av $\angle$ C.

I $\mathrm{\Delta }$ABC er $\angle$A = 90°, AC = 6 cm, BC = 10 cm. Punktet D er midtpunktet på hypotenusen, og normalen fra D på AB treffer AB i fotpunktet E. Finn arealet av firkant AEDC.

a) I trekant PQR er PQ= 65, QR = 33 og PR =56. Undersøk om trekanten er rettvinklet.

b) Regn ut vinkel P.

c) Regn ut høyden fra hjørnet R på siden PQ

Anta at vi har en trekant med vinkler på ${30}^o$, ${60}^o$ og ${90}^o$. Den største kateten er $a$, den minste kateten er $b$ og hypotenusen kalles $c$.

a) Bruk trekanten til å vise at $\cos \left({30}^o\right)=\sin \left({60}^o\right)$ og at $\sin \left({30}^o\right)=\cos \left({60}^o\right)$.

b) I en ${30}^o,{60}^o,{90}^o$-trekant er den korteste kateten halvparten så lang som hypotenusen, altså er $b=\frac{1}{2}c$. Hvor stor blir $a$ uttrykt ved $c$ ?

c) Vis at $\sin \left({30}^o\right)=\frac{1}{2}$ og at $\sin \left({60}^o\right)=\frac{\sqrt{3}}{2}$.