Øvingsoppgaver med fasit
Lenke til dette oppgavesettet (kan bokmerkes)Oppgaver
1
Tegn grafen til funksjonen nedenfor på lommeregneren i det oppgitte området. Bestem x-verdiene til alle skjæringspunkter i med x-aksen.
2
a) Skriv
som en differanse mellom to kvadrater ved å danne et fullstendig kvadrat av .
b) Faktoriser uttrykket du fant i a) ved hjelp av konjugatsetningen. Vis at du får .
c) Sett utenfor en parentes og bygg ut et fullstendig kvadrat av slik at
blir skrevet som et produkt av og en differanse mellom to kvadrater.
d) Vis at et generelt andregradsuttrykk kan faktoriseres ved
,
der og er nullpunktene til polynomet.
3
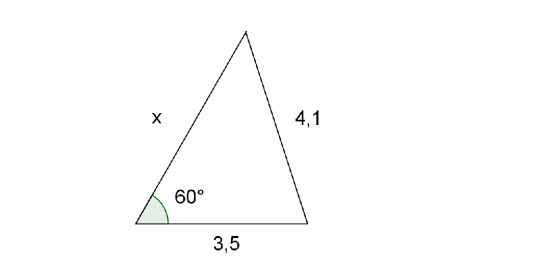
Vis ved hjelp av cosinussetningen at lengden på figuren oppfyller andregradslikningen
.
Finn ved hjelp av løsningsformelen for andregradslikninger.
4
Løs andregradsligningen og sett prøve på svaret.
5
Siv har 400 kroner til å bruke på telefonregning. Hun betaler 339 kroner i fast månedspris og 0,39 kr per sms, mens all ringing er gratis. Sett opp en funksjon som viser hvor mye penger det er igjen etter x meldinger. Hvor mange dager tar det før Siv har brukt opp 400 kroner hvis hun sender 15 meldinger hver dag?
6
Løs følgende ligninger ved regning. Det er ikke sikkert at alle ligningene har løsning.
a)
b)
c)
7
Løs likningen ved regning:
(3x + 1)2 = 36
8
a) Løs ligningen grafisk på kalkulatoren og ved regning når .
b) Ligningen i a) har 2 løsninger når . Bestem slik at ligningen bare får èn løsning.
9
Løs likningen ved hjelp av løsningsformelen for andregradslikninger:
5x2 - x = 0
10
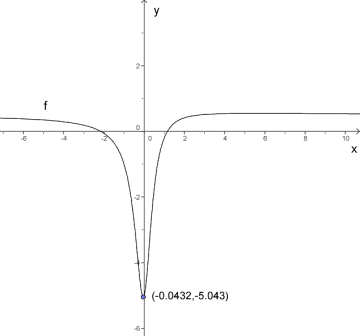
Vi skal undersøke funksjonen .
a) Tegn grafen til funksjonen på lommeregneren.
b) Bestem nullpunktene til funksjonen ved regning.
c) Bestem bunnpunktet til funksjonen grafisk på lommeregneren.
d) Hva vil gå mot hvis blir svært stor?
Fasit
1
x = -1, x = 1
2
a)
c)
3
4
x=2 eller x = -3
5
Etter 3 dager.
6
a) og
b) og
c) ingen reelle løsninger
7
x = eller x =
8
a)
b) ligningen har alltid to løsninger
9
10
a) Figuren viser grafen til .
b)
c)
d)