Øvingsoppgaver med fasit
Lenke til dette oppgavesettet (kan bokmerkes)Oppgaver
1
Funksjonen f er gitt ved:
a) Finn bruddpunktet.
b) Bruk lommeregneren til å finne ut hva som skjer med funksjonsverdiene for store tallverdier av x.
2
Vis uten regning at likningen ikke har noen reelle løsninger.
3
En mann har 40 meter med ståltråd som han skal bruke til å avgrense et rektangulært område til blomsterbedd. Ståltråden skal brukes på tre av sidene, mens den fjerde siden vil huset være. Hva er det største arealet som blomsterbeddet kan ha? Løs oppgaven grafisk.
4
Tegn grafen til andregradsfunksjonen og finn nullpunktene ved hjelp av grafen.
5
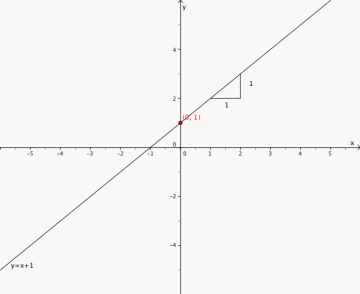
Bruk stigningstallet og konstantleddet til å tegne linjen.
6
Tegn linjen på lommeregneren når x er et tall mellom -5 og 5
7
Tegn linjen på lommeregneren når x er et tall mellom -5 og 5
8
Funksjonen f er gitt ved
a) Tegn grafen til f.
b) Finn bunnpunktet til f.
9
La være funksjonen .
a) Hva er for og ?
b) Tegn grafen for .
c) Hva er skjæringspunktene mellom og linja ? Løs grafisk og ved regning.
10
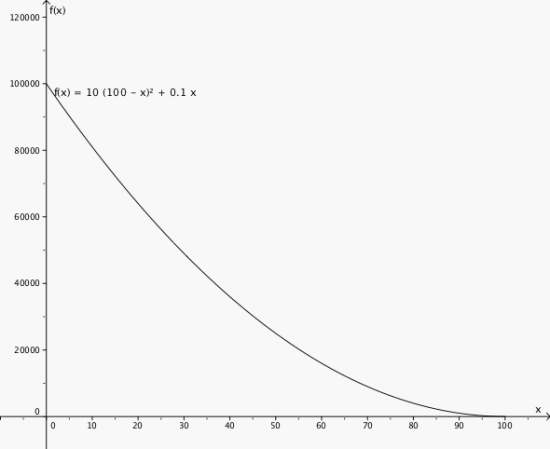
Funksjonen er gitt ved
a) Tegn grafen til A.
b) Finn den momentane veksthastigheten når x = 0.5.
Fasit
1
a) bruddpunkt x=2
2
Tegn grafen og da ser du at grafen ikke skjærer y - aksen.
3
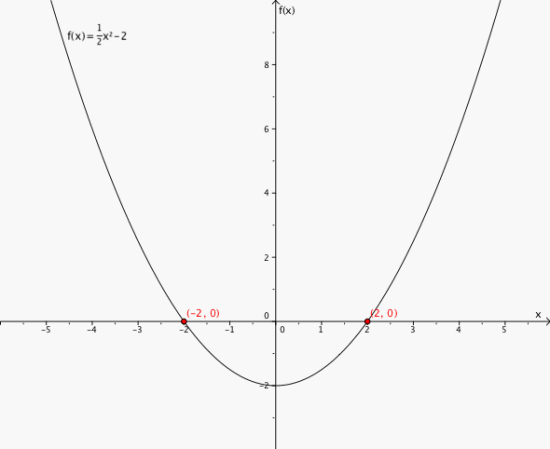
4
x = 2 og x = -2
5
Stigningtall: 1
Konstantledd: 1
6
7
8
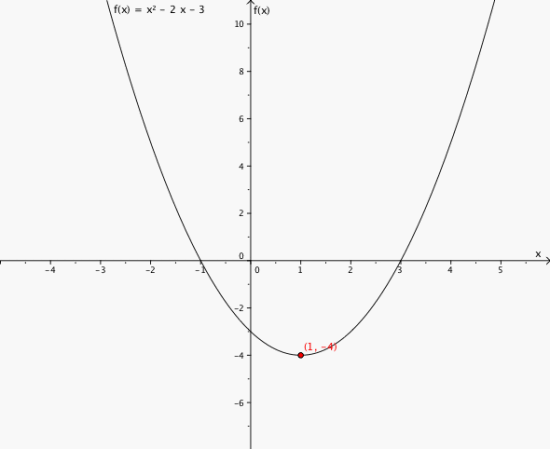
a)
Grafen til f(x) og bunnpunktet (1,-4)
b) Bunnpunkt (1,4)
9
a) og
b)
c)
10
a)
b) -1990

![Figuren viser grafen til f(x) for x i intervallet [-5,5]. Den grafiske løsningen av likningen f(x)=3 er også angitt.](/aim/matematikk/files/9/c/a/a86060e8e4a09402a2b0cec2f7c0a518d238b981c4/9caa86060e8e4a09402a2b0cec2f7c0a518d238b981c4.gif/Scale?geometry=360x600>)