Øvingsoppgaver med fasit

Finn nullpunktene til funksjonen

$y=5x^2-9x+4$

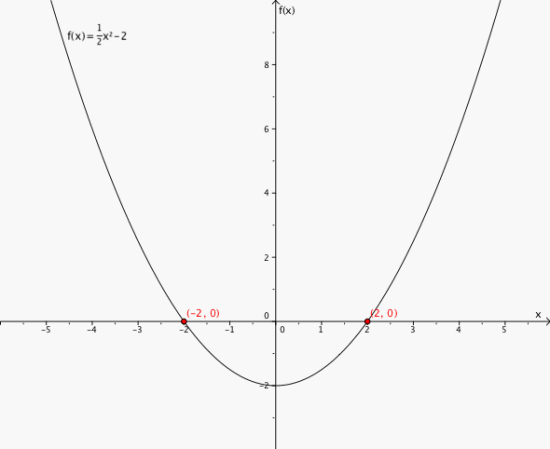
Tegn grafen til andregradsfunksjonen og finn nullpunktene ved hjelp av grafen.

$h\left(x\right)=\frac{1}{2}{x}^2-2$

Siv har 400 kroner til å bruke på telefonregning. Hun betaler 339 kroner i fast månedspris og 0,39 kr per sms, mens all ringing er gratis. Sett opp en funksjon som viser hvor mye penger det er igjen etter x meldinger. Hvor mange dager tar det før Siv har brukt opp 400 kroner hvis hun sender 15 meldinger hver dag?

Hvor mange nullpunkter har funksjonen $x^2-2x+4$? Begrunn svaret.

Funksjonen $f$ er gitt ved $f\left(x\right)=-{(x-3)}^2+5$.

a) Finn toppunktet ved regning.

b) Finn nullpunktene og skjæringspunktet med $y$-aksen.

c) Finn skjæringspunktene til $f$ med funksjonen $g\left(x\right)=2x^2-4$ ved regning.

d) Hva er symmetriaksene til $f$ og $g$ ?

Velg ulike tredjegradsfunksjoner slik at grafen får tre nullpunkter, to nullpunkter og ett nullpunkt

Bruk et digitalt hjelpemiddel til å tegne grafen til

$f\left(x\right)=x^2$. Les av koordinatene til nullpunktet til f(x).

La $f$ være funksjonen $f\left(x\right)=2x^4-3x^2-5$.

a) Finn nullpunktene til $f$ ved regning.

b) Finn funksjonens topp- og bunnpunkter ved regning.

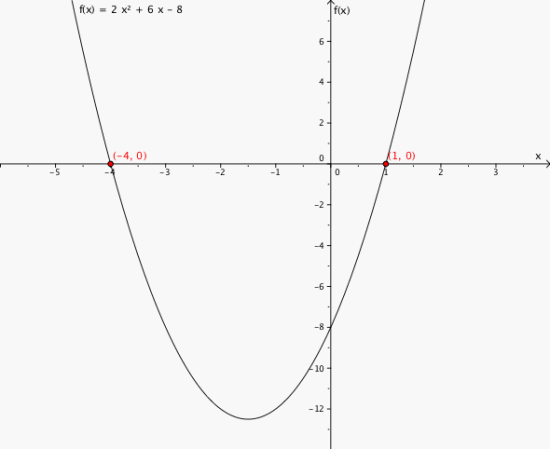
Tegn grafen til andregradsfunksjonen og finn nullpunktene ved hjelp av grafen.

$g\left(x\right)=2x^2+6x-8$

Undersøk ved å tegne grafen om funksjonen f gitt ved $f\left(x\right)=2x^2+4x+3$ har nullpunkter.

b) Finn en verdi for c som gjør at funksjonen f gitt ved $f\left(x\right)=2x^2+4x+c$ har
1) To nullpunkter 2) Ett nullpunkt.

Det er lov å prøve seg fram på digitalt verktøy.