Øvingsoppgaver med fasit

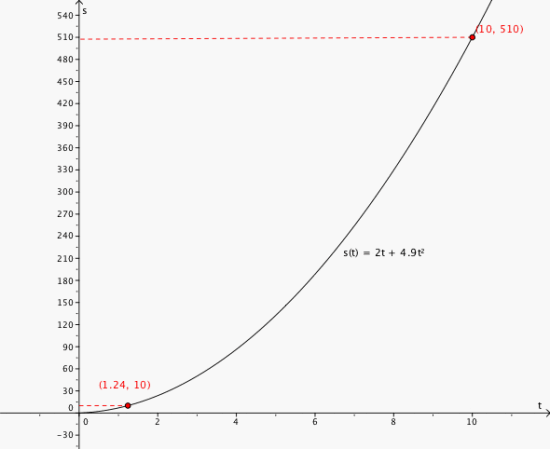
Fallstrekningen s meter etter t sekunder for en stein som blir kastet loddrett nedover,  er gitt ved $s\left(t\right)=2t+4.9t^2$. Finn grafisk og ved regning hvor langt ned steinen har falt etter 10 sekunder og hvor lang tid det tar før steinen har falt 10 meter. Finn den momentane veksthastigheten når t = 5. Hva betyr dette?

Finn den deriverte for x = 2.

$f\left(x\right)={2x}^3+x^2-4x+5$

La $y=3x^2+2x$ beskrive en kurve. Bestem den gjennomsnittlige hastigheten til funksjonen mellom $x_1=-1\text{ og }{x}_2=1$.

Linjen $y=kx+m$ er sekant til $f\left(x\right)=2^{0,5x}$. Skjæringspunktene har y-koordinatene 1 og 10. Finn likningen til sekanten og vis at f(x) ikke kan ha to sekanter som står vinkelrett på hverandre.

Funksjonen $g\left(x\right)={-x}^2-10$ har sekant som går gjennom punktene $(1,-11)\text{ og }(3,-19)$. Finn likningen til sekanten.

Funksjonene f og g er gitt ved

$\begin{array}{c}f\left(x\right)=15\cdot {0.91}^x\\ g\left(x\right)=15\cdot {0.98}^x\end{array}$

Finn den momentane veksthastigheten for grafen til begge funksjonene for x = 3

Funksjonen f er gitt ved $f\left(x\right)=2x^2+x-4$. Finn den momentane veksthastigheten både ved regning og ved hjelp av digitalt verktøy når:

a) $x=2$
b) $x=-2$ 
c) $x=3$

Klaras mormor har satt in 10 000 kr i en fond som har vokst med 6 % hvert år i 5 år. Bestem den gjennomsnittlige veksten uttrykt i kroner per år.

Hvordan finner du den gjennomsnittlige veksthastigheten til en funksjon?

Funksjonen f gitt ved $f\left(x\right)=-0.017x^2+1.6x+4.9$ beskriver antall tusen fluer i Norge i årene 1970 - 2000.

Bestem den gjennomsnittlige veksthastigheten per år fra 1980 til 1990.