Øvingsoppgaver med fasit
Lenke til dette oppgavesettet (kan bokmerkes)Oppgaver
1
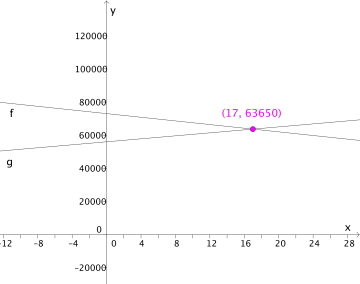
Antall innbyggere i byen A var 73 000 i 2000. Fra 2000 sank innbyggertallet med omtrent 550 per år. Antall innbyggere i byen B var 56 000 i 2000. I denne byen økte antall innbyggere med omtrent 450 per år. Sett opp matematiske modeller for folketallet i de to byene og finn ut når det er like mange innbyggere i disse to byene.
2
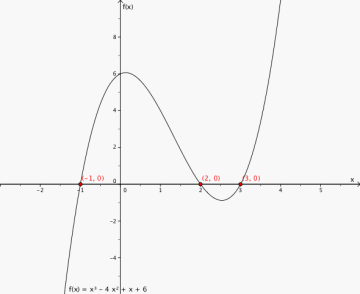
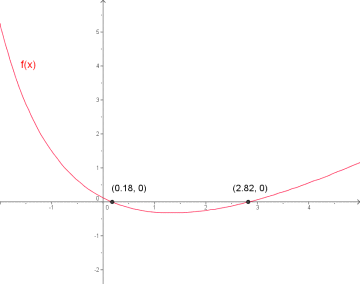
Løs tredjegradsligningen grafisk:
3
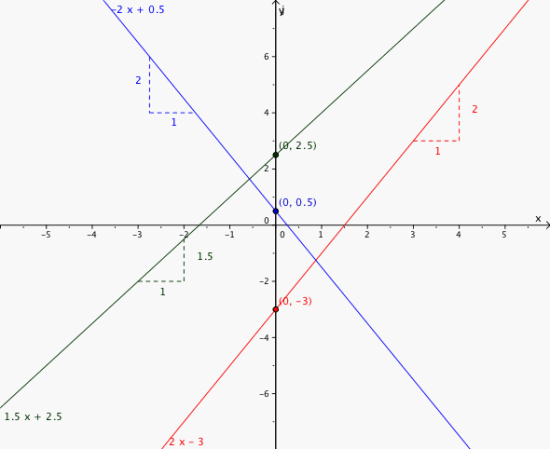
Benytt det du har lært om konstantleddet og stigningstallet til å tegne de rette linjene gitt ved:
4
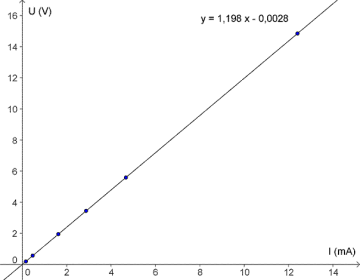
I et fysikk-forsøk skal sammenhengen mellom strømmen gjennom og spenningen over en motstand bestemmes. Måleresultatene er gitt i tabellen under.
a) Tegn inn punktene i et koordinatsystem med langs førsteaksen og langs andreaksen. Tilpass ei rett linje til punktene ved lineær regresjon på lommeregneren. Hva er likningen til linja?
b) Argumenter for at sammenhengen mellom strømmen gjennom og spenningen over motstanden er gitt ved Ohms lov:
Hva var verdien av i dette forsøket (gi svaret i )?
5
Gitt funksjonen .
a) Tegn grafen i intervallet på lommeregneren.
b) Hva er den naturlige definisjonsmengden til funksjonen?
c) Bestem nullpunktene grafisk på lommeregneren og ved regning.
6
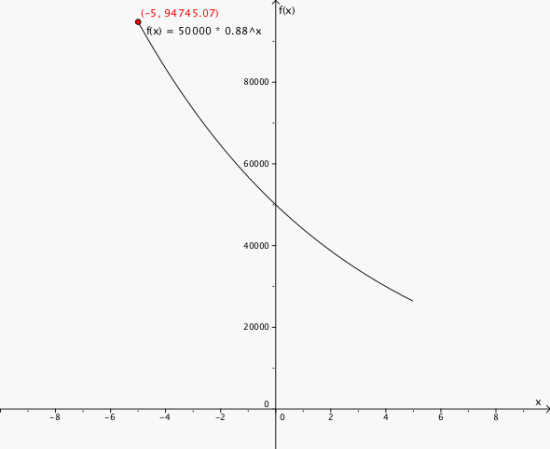
En fem år gammel moped er i år verdt 50 000 kroner. Siden mopeden var ny, har verdien sunket med omtrent 12% per år. Vi regner med at verdien av mopeden i de neste 10 år kommer til å fortsatte og synke med 12 % per år.
a) Forklar hvorfor funksjonen f gitt ved er en matematisk modell for verdien av bilen om x år.
b) Vis at bilen kostet omtrent 95 000 kroner da den var ny.
c) Tegn en graf som viser prisutviklingen til bilen fra den var ny og til den blir 10 år gammel.
7
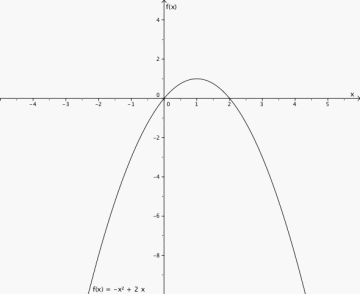
Tegn grafen til funksjonen
a) Finn stigningstallet for tangentene i punktene (0,0), (1,1), (2,0).
b) Finn ligningene til de tre tangentene.
8
9
Løs likningen ved hjelp av digitale verktøy og ved regning.
10
Tegn grafen ved hjelp av et digitalt verktøy og finn koordinatene til eventuelle topp- og bunnpunkter for følgende funksjon:
Fasit
1
Etter 17 år, dvs. i 2017 vil innbyggertallet være likt i de to byene.
2
3
4
a) (på lommeregneren TI-83)
b)
5
a)
b)
c)
6
7
a) 2, 0 og -2
b) y = 2x, y = 1 og y= -2x+4
8
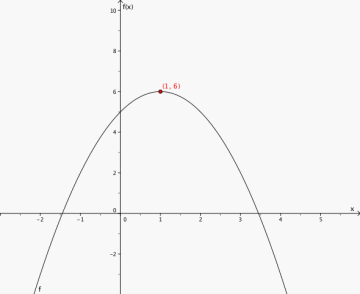
Toppunkt (1,6)
Grafen stiger når x<1
Grafen synker når x>1
9
10
toppunkt:
bunnpunkt: