Øvingsoppgaver med fasit

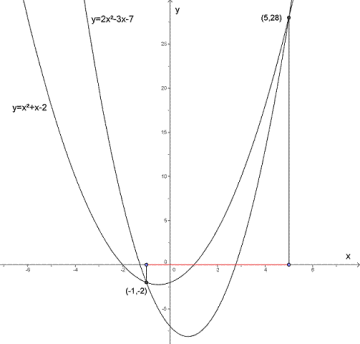
Finn skjæringspunktene til de to parablene gitt ved

$\begin{array}{c}f\left(x\right)=\frac{1}{2}{x}^2-2\\ g\left(x\right)=2x^2+x-1\end{array}$

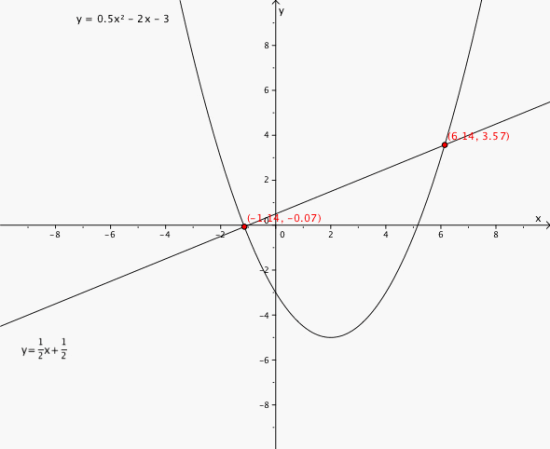
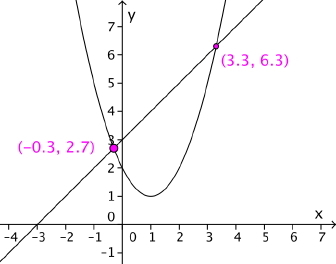
Hvordan finner du skjæringspunkt mellom en lineær funksjon og en andregradsfunksjon?

Bestem a og b slik at funksjonene

$$\begin{gathered} f\left(x\right)=ax+b \\ g\left(x\right)=3x-5 \end{gathered}$$

har uendelig mange skjæringspunkter.

Finn to funksjoner som har skjæringspunktene $(-5,0),(1,0)$.

Familien Leierud skulle leie bil. På et sted var leieprisen 300 kr døgnet og i tillegg 1 kr pr kjørte km. Et annet sted tilbød en leiepris på 150 kr døgnet og i tillegg 2,50 kr pr kjørte km. Familien regnet med å ha bilen i 10 døgn.

Sett opp funksjonsuttrykk for de to alternativene. Framstill resultatene i et felles koordinatsystem.

Når lønner de forskjellige alternativene seg?

Løs også som likning og ulikhet.

Undersøk grafisk om ligningssystemet har løsning.

$\begin{array}{c}-0.5x^2+2x+y=-3\\ y-\frac{1}{2}x=\frac{1}{2}\end{array}$

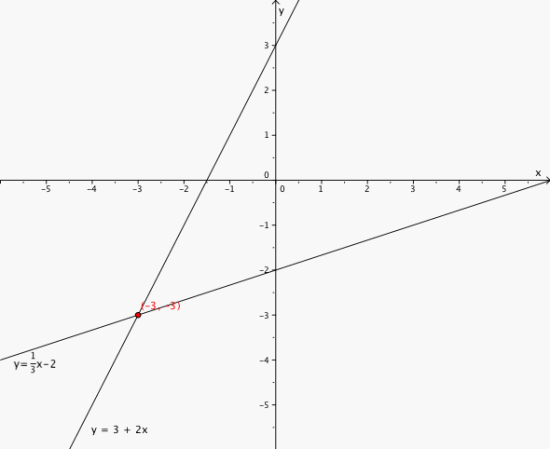
Løs ligningssystemet grafisk:

$\begin{array}{c}y=x^2-2x+2\\ -x+y=3\end{array}$

Løs ligningssettet grafisk:

$\left[\begin{array}{c}-2x+y=3\\ \frac{1}{3}x-y=2\end{array}\right]$

To andregradsfunksjoner har alltid to skjæringspunkter. Er påstanden riktig? Begrunn svaret.

Løs ulikheten ved regning. Kontroller deretter grafisk på kalkulatoren.

    $2x^2-3x-7<x^2+x-2$