Korrelasjon og årsakssammenheng

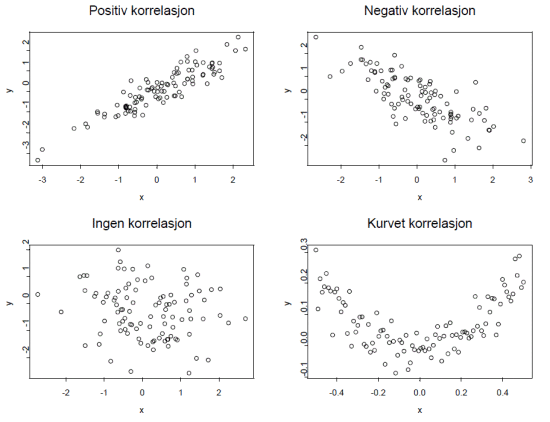
Et mye brukt mål innen statistikk er korrelasjon, et matematisk mål på sammenhengen mellom to variable størrelser. Korrelasjonen angis som et tall mellom –1 og 1 (evt. –100% og 100%). Det er et standardisert mål og derfor uavhengig av benevning (i motsetning til kovarians). Positiv korrelasjon indikerer at de to variable størrelsene varierer i takt, mens negativ korrelasjon indikerer at de to variable størrelsene varierer i utakt. Figur 1 viser eksempler på to variable x og y som er positivt korrelert, negativt korrelert, ukorrelert og korrelert på en mer komplisert måte.

En vanlig felle å gå i, er å ta korrelasjon som bevis på at det foreligger en årsakssammenheng. Denne misforståelsen gir ofte opphav til underlige presseoppslag. For å gjøre det helt klart;

korrelasjon og årsakssammenheng er ikke det samme!

Korrelasjon er kun et numerisk mål på om to datasett varierer i takt. At noe varierer i takt betyr ikke at det er en årsakssammenheng. Det finnes mange eksempler fra media der dette er misforstått, og vi viser et par eksempler under.

Figur 1: Ulik korrelasjon mellom to variable størrelser. x og y.

Figur 1: Ulik korrelasjon mellom to variable størrelser, x og y.

Eksempel 1: Tannlegebesøk og hull

Figur 2: Tannlegebesøk og hull. Fra Aftenposten 2. oktober 1998.

Figur 2 viser en artikkel der det står at de som går oftere til tannlegen, har flere hull. Oppslaget er basert på en undersøkelse, der antall hull og tannlegebesøk er sammenlignet med hverandre og en sammenheng mellom de to størrelsene er avdekket. I ingressen til artikkelen står det at:

"De som har holdt seg unna tannleger i minst fem år, har færre hull og reparasjoner i tennene enn de som besøker tannlegen opptil hvert halvår."
 
En kan tenke seg at resultatene fra undersøkelsen kan vises som på øverste figur til venstre i figur 1, der x er antall hull og y er antall tannlegebesøk. Mange hull og mange tannlegebesøk henger sammen, på samme måte som få hull og få tannlegebesøk gjør det samme. Noen har deretter trukket en (litt for rask) slutning om at man får flere hull av å gå til tannlegen. Dette er åpenbart feil. Hvorfor er det slik at mange hull og hyppige tannlegebesøk henger sammen? Fordi oftere tannlegebesøk gir flere hull? Nei, man går nok oftere til tannlegen fordi man har mange hull. 

Eksempel 2: Bilfarge og ulykkesfrekvens

Figur 3 viser en artikkel som hevder at sølvfargede biler er tryggest i trafikken, en konklusjon fra en undersøkelse der bilulykker og biltyper er sammenlignet med hverandre. I undersøkelsen kom det også fram at brune biler kom verst ut i ulykkesstatistikken. Er det virkelig slik at sølvfargen på bilen din garderer deg mot alvorlige ulykker? Er sjansen større for å komme utfor en ulykke i en brun bil? Eller kan det tenkes at nye biler, som er sikrere, ofte er sølvfarget, mens eldre biler ofte er brune?  

Eksempel 3: Trafikkdrepte og rentenivå

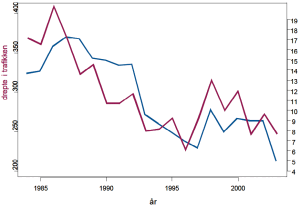
Figur 4 viser antall drepte i trafikken og rentenivået de siste 20 åra.  

Figur 4: Trafikkdrepte og rentenivå (Kilde: SSB)

Sammenhengen mellom de to størrelsene er påfallende, de varierer fint i takt og det er en sterk positiv korrelasjon. Er det opplagt at det skal være en sammenheng her? Eller er den tilfeldig? Og betyr denne sammenhengen at det er en årsakssammenheng mellom rentenivå og trafikkdrepte? Er det virkelig slik at sentralbanksjefen kan knipse med fingrene og på den måten regulere antall drepte i trafikken?

Eksempel 4: Matematikkprestasjoner og skonummer

Anta at vi finner en høy korrelasjon mellom skonummer og matematikkprestasjoner i en matematikktest for barn. Det er lite trolig at noen skårer høyt fordi de har store sko, ei heller at de har store sko fordi de er gode i matematikk. Å kjøpe større sko til en svak elev vil neppe være til særlig hjelp i matematikk! Trolig er det slik at alder er en viktig tredje variabel som påvirker begge, altså at både skonummer og kunnskaper i matematikk øker med alderen.

Hvordan påvise en årsakssammenheng?

For å finne ut om noe (årsak) fører til noe annet (effekt), må det foreligge en statistisk sammenheng (korrelasjon) mellom årsaksvariabelen og effektvariabelen. Det må være en bestemt tidsrekkefølge mellom variablene; årsak må komme før effekt. Videre må man påvise at den statistiske sammenhengen ikke er falsk. Den må ikke være tilfeldig og det må ikke være en bakenforliggende faktor som påvirker både årsak og effekt samtidig. Dette er det vanskelige punktet!

Små sannsynligheter, sjeldne begivenheter

Mange fenomener karakteriseres som sjeldne, for eksempel å vinne i lotto eller å få en spesiell sykdom. Sannsynligheten for at disse fenomenene inntreffer er liten, og det er vanskelig å jobbe vitenskapelig med dem fordi datagrunnlaget er lite (det har skjedd sjelden). Slutninger og estimater blir derfor beheftet med stor usikkerhet.

Når et sjeldent fenomen inntreffer, blir det ofte store oppslag i media. Et eksempel på dette er Sømnasaken. Det ble observert tre tilfeller av hjernesvulst i Sømna kommune i 1992, noe som var uvanlig mange i en så liten kommune. Saken vakte stor oppsikt i media og blant politikere, og saken ble sett i sammenheng med Tsjernobyl-ulykken, se figur 5.

Figur 5: Sømnasaken (Dagbladet 10. og 11. januar 1993)

Etter Kreftregisterets statistikk vil man for en kommune av Sømnas størrelse og befolkningssammensetning i gjennomsnitt observere et tilfelle av hjernesvulst hvert sjette år hvis kreftrisikoen er som i resten av landet. Sannsynligheten for å observere tre eller flere tilfeller i løpet av et år er bare 0,6 promille (6 av 10000). Det ble satt i gang undersøkelser for å finne eventuelle årsaker til krefttilfellene i Sømna.

Som et regneeksempel tenker vi oss at vi har 100 kommuner med samme størrelse og befolkningsstruktur som Sømna, og at vi observerer antall krefttilfeller i disse kommunene i en tiårsperiode. Da er det 45% sannsynlig at vi i minst én av kommunene vil oppleve minst tre krefttilfeller i løpet av et år ved en ren tilfeldighet.