Jacob (Jacques) Bernoulli

Jacob (Jacques) Bernoulli
Jacob Bernoulli ga betydningsfulle bidrag i mange grener av matematikken. Han fant en lov om store tall i sannsynlighetsteori. I geometri så han på brennkurver, og spesielt de forbundet med kurver til parabolen, den logaritmiske spiralen og episykloiden.
Faren til Jacob Bernoulli, Nicolaus Bernoulli, var en betydningsfull borger av Basel som var medlem av byrådet og forhørsdommer. Moren til Jacob Bernoulli kom fra en betydningsfull familie i Basel bestående av bankfolk og lokale byrådsmedlemmer. Jacob Bernoulli var broren til Johann Bernoulli og onkelen til Daniel Bernoulli.
Han ble oppmuntret til å studere filosofi og teologi av foreldrene sine, som han ikke hadde noe til overs for. Han ble uteksaminert fra Universitetet i Basel i 1671 med en MA i filosofi, og senere med en licentiat (autorisert utøver) i teologi i 1676. Mens han studerte mot graden sin leste også Jacob Bernoulli matematikk og astronomi, mot sine foreldres ønsker. Dette er typisk for mange i Bernoullifamilien, som valgte å gå imot familiens ønsker ved å studere matematikk fremfor å få en karriere innen et annet område.
I 1676, etter å ha fullført teologigraden sin, flyttet Bernoulli til Geneve hvor han jobbet som lærer. Han reiste så til Frankrike hvor han studerte sammen med tilhengerne av Descartes, som på den tiden ble ledet av Malebranche.
I 1681 reiste Bernoulli til Nederland hvor han møtte mange matematikere, inkludert Hudde. Han fortsatte å studere med de ledende matematikerne og vitenskapsmennene i Europa. På denne tiden interesserte han seg for astronomi, og lagde et arbeid som gav en feilaktig teori om kometer.
Reisene hans medførte at han innledet korrespondanser med mange matematikere, som han fortsatte med i mange år. Jacob Bernoulli vendte tilbake til Sveits, og underviste mekanikk på Universitetet i Basel fra 1683.
I 1684 giftet Jacob Bernoulli seg med Judith Stupanus. De fikk to barn, en sønn som ble gitt bestefarens navn Nicolaus og en datter. Disse barna, i motsetning til de fleste i Bernoullifamilien, ble ikke matematikere eller fysikere.
En av de mest betydningsfulle hendelser i Jacob Bernoullis matematiske studier inntraff da hans yngre bror Johann Bernoulli begynte å jobbe med matematiske emner. Selv om både Jacob og Johann Bernoulli jobbet med lignende problemer forandret raskt forholdet dem imellom seg fra et samarbeid til en rivalisering som førte til et fullstendig brudd i forholdet i 1697. Krangelen mellom de to brødrene over hvem som kunne få størst anerkjennelse var selvfølgelig tåpelig, siden begge kom med bidrag til matematikken av største betydning.
Jacob Bernoulli gav betydningsfulle bidrag i mange grener av matematikken. Innen 1689 utgav han arbeider om uendelige rekker og sin lov om store tall i sannsynlighetsteori. Tolkningen av sannsynlighet som relativ frekvens sier at hvis et eksperiment gjentas mange ganger er den relative frekvensen til hendelse lik sannsynligheten for den hendelsen. Loven for store tall er en matematisk tolkning av dette resultatet.
I geometri så han på brennkurver, og spesielt de forbundet med kurver til parabolen, den logaritmiske spiralen og episykloiden. Lemniskaten til Bernoulli ble først påtenkt av Jacob Bernoulli i 1694.
I 1695 så han på vindebru-problemet, som går ut på å finne en kurve som er slik at vekten som glir langs kabelen alltid holder vindebrua i balanse. I 1696 løste han differensialligningen som nå kalles Bernoulliligningen'':
Jacob Bernoullis mest originale arbeid var "Ars Conjectandi" gitt ut i Basel i 1713, åtte år etter hans død. Arbeidet var uferdig da han døde, men det er fremdeles et arbeid av stor betydning innen sannsynlighetsteorien.
Del på Facebook
Begrep
-
Episykloide
Den plane kurven et fast punkt på en sirkel beskriver når sirkelen ruller langs ytterkanten av en fast sirkel.
-
Geometri
Ordet kommer fra gresk og betyr jordmåling. Geometri er den delen av matematikken som handler om egenskaper, form og størrelser til 2D- og 3D-figurer. Geometrien ser på sammenhenger mellom vinkler, sider, sideflater og kanter, som gjør at vi kan utføre ulike beregninger med de ulike figurene.
-
Lemniskate
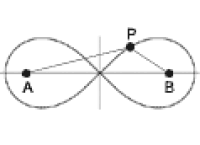
Lemniskaten er en lukket kurve som ser ut som et liggende 8-tall. Den kan i polarkoordinater angis
som r = p√(cos2θ).
Lemniskaten kan beskrives på liknende måte som ellipsen. Gitt to brennpunkter A og B med avstand 2a. Lemiskaten er da de punkter P som tilfredstiller at PA·PB = a2. -
Logaritmisk spiral
En spiral er en kurve som snor seg om et fast punkt P. Beliggenheten til et punkt S på spiralen kan beskrives ved å angi retningen fra P til S angitt som vinkelen θ fra førsteaksen og avstanden fra P til S angitt som r. For en logaritmisk spiral tilfredstiller punktene på spiralen lnr = aθ, der a er et reelt tall.
-
Sannsynlighetsteori
Undersøkelser av mulige utfall av gitte begivenheter sammen med deres relative sannsyligheter og forekomster. Det er faktisk betydelig uenighet omkring nøyaktig hva sannsynlighet betyr i praksis. Noen matematikere anser det bare som en komponent i en abstrakt teori, mens andre gir det en tolkning basert på frekvensen av visse utfall.
-
Uendelige rekker
En rekke er en sum av elementene i en tallfølge. Rekken kalles uendelig hvis den består av uendelig antall elementer.
Eksempel :
( ∞ er tegnet for uendelighet )
Omtalt person







