Trigonometriske likninger
I denne seksjonen skal vi se på trigonometriske likninger, altså likninger som involverer
Trigonometriske funksjoner
Funksjonene sinus, cosinus, tangens og cotangens. Defineres enklest for en spiss vinkel i en rettvinklet trekant som forholdet mellom to av sidene i trekanten.
Radianer
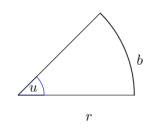
Det absolutte vinkelmålet til vinkelen er tallet der er buelengden og er radien. Legg merke til at siden både og er lengder, vil lengdebenevningene forkortes mot hverandre i brøken , slik at det absolutte vinkelmålet blir et ubenevnt tall. Likevel sier vi ofte at er målt i radianer.
I en sirkel med radius er omkretsen lik . Det er derfor naturlig å si at en runde i sirkelen tilsvarer radier eller radianer.
Eksempel 1
Vi løser likingen . Om vi trekker fra og dividerer med , får vi . Taster vi inn på kalkulatoren, får vi . Speiler vi denne vinkelen om -aksen, får vi . I tillegg vil alle omløp av disse vinklene være løsninger, så den generelle løsningen er for alle heltall . Det er vanlig å skrive løsningen slik at de første tallene er i intervallet (første omløp):
Eksempel 2
Vi løser likningen . Da er , og taster vi inn på kalkulatoren , får vi løsningen . Speilingen om -aksen har samme cosinusverdi, så er også en løsning. I tillegg kommer alle omløp av disse til å være løsninger, så den generelle løsningen er for alle heltall .
Eksempel 3
Vi løser likningen Da er , så vi får løsningen . Husk at Om vi roterer vinkelen , altså radianer, vil forholdet mellom første og andre-koordinatet på enhetssirkelen forbli det samme. Dermed er for alle heltall og den generelle løsningen er for alle heltall .
Eksempel 4
Vi løser likningen Setter vi , får andregradslikningen Denne har løsninger og slik at Vi vet at cosinus kun gir verdier i det lukkede intervallet , så vi kan ignorere den andre løsningen. Da står vi igjen med . Bruker vi på kalkulatoren, får vi Speiling om -aksen gir løsningen . I tillegg vil alle omløp av disse være løsninger. Da får vi den generelle løsningen
Eksempel 5
Et bioteknologisk selskap skal gå til innkjøp av nytt utstyr. Fordi prisen på utstyret varierer svært mye med tiden, setter de opp en modell med at prisen på utstyret etter år kommer til å være hvor er pris i millioner. Selskapet vil kjøpe utstyret så billig og så fort som mulig. Når skal de gå til utstyrsinnkjøp?
Vi vet at den minste verdien til er . Dermed er den minste verdien til lik . Den laveste prisen til produktet er derfor en million ( ikke kan bli mindre enn ). For å finne ut når denne prisen inntreffer, må vi løse likningen for tiden .
Vi skriver dette om til , som gir løsningen for alle heltall . Den minste positive verdien for får vi ved å se på , altså når .
Svaret er at ifølge deres modell tar det litt over 3 år før selskapet bør gå til innkjøp av utstyret.
Del på Facebook
Lynkurs 11.-13.trinn
Trigonometri
Består av:
- Trekanter
- Sinus, cosinus og tangens
- Eksakte verdier
- Klara finner eksakte verdier
- Trigonometriske formler
- Grafene til sin x, cos x og tan x
- Arealsetningen
- Sinussetningen
- Cosinussetningen
- Trigonometriske likninger
- Mer kompliserte likninger
- Periodiske funksjoner
- Derivasjon av trigonometriske funksjoner
- Omskriving til standardform




