Derivasjon av vektorfunksjoner 2 - vektorfunksjoner

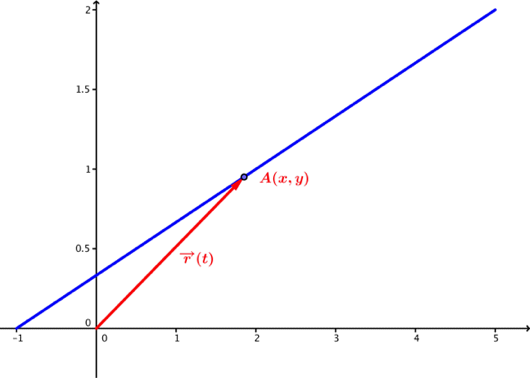
Anta at vi har en parameterframstilling av en linje i planet, for eksempel:

$K: \begin{array}{c}x\left(t\right)=2+3t\\ y\left(t\right)=1+t \end{array}, t\in \left[-1,1\right]$

For hver $t$ har vi da et punkt $A\left(x,y\right)$ på linja og vi kan definere en vektor fra origo $O$ til punktet:

            $\overrightarrow{OA}=\left[x,y\right]=\left[2+3t,1+t\right]$

Denne vektoren kalles posisjonsvektoren. Vi kan nå definere

            $\overrightarrow{r}\left(t\right)=\left[2+3t,1+t\right], t\in \left[-1,1\right]$

$\overrightarrow{r}\left(t\right)$ er da vektorfunksjonen som for hver $t$, gir en vektor fra origo til linjestykket.

For hver $t$ i $\left[-1,1\right]$ gir $\overrightarrow{r}\left(t\right)$ en vektor fra origo til et punkt på linja, så hvis vi varierer $t$, varierer endepunktet på vektoren. Vi sier at linja er grafen til vektorfunksjonen, og de to funksjonene

$\begin{array}{c}x\left(t\right)=2+3t\\ y\left(t\right)=1+t \end{array}$

er koordinatfunksjonene til $\overrightarrow{r}\left(t\right)$.

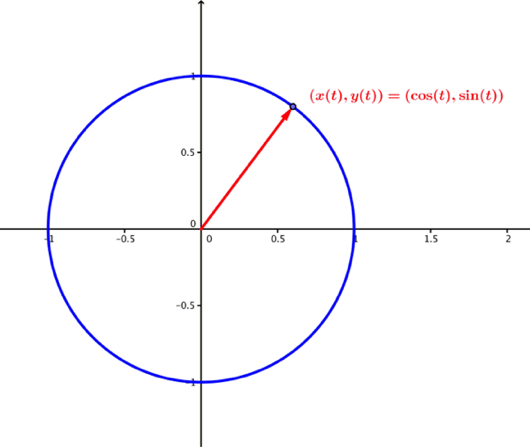
Eksempel

Vektorfunksjonen

$\overrightarrow{r\left(t\right)}=\left(\cos \left(t\right),\sin \left(t\right)\right), t\in \left[0,2\pi \right]$

gir følgende vektorer:

 Den blå sirkelen er kurven som vektorene "peker på".