Deriverbarhet
Definisjon
Vi sier at en funksjon er deriverbar i et punkt , hvis grensen under finnes:
Men når er det denne grensen ikke finnes? I denne seksjonen skal vi se på når den deriverte finnes, og vise noen eksempler.
Definisjon. Grenser ovenfra og nedenfra
Vi skriver
for grensen til når går mot ovenfra, og
for grensen til når går mot nedenfra.
Teorem. Deriverbarhet
En funksjon er deriverbar i et punkt hvis
- Funksjonen er i ,kontinuerlig
Kontinuerlig funksjon
En kontinuerlig funksjon er en sammenhengende graf, det vil si at grafen danner en sammenhengende kurve.
- .
Eksempel 1 – en funksjon som er deriverbar på hele tallinja.
La oss se på i et punkt tilfeldig punkt :
Vi ser at grensen finnes, og dermed er funksjonen deriverbar i . Siden kan være hvilket tall som helst, er deriverbar for alle .
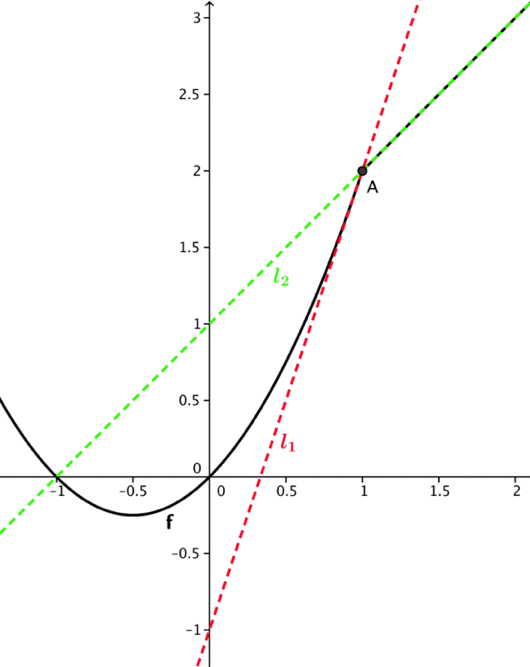
Eksempel 2 – en funksjon med et ikke-deriverbart punkt:
I eksempelet under ser vi en funksjon med en «knekk». Hva skjer med den deriverte i dette punktet? Vi husker at den deriverte er lik stigningstallet på tangenten til kurven. I dette tilfellet ser vi at vi får vanskeligheter med å avgjøre hva tangenten er i punktet , vi får rett og slett forskjellige tangenter avhengig av hvilken side vi kommer fra.
La oss se hva som skjer med funksjonen:
Hvis vi deriverer hver av sidene, ser vi at vi får at den deriverte er for mindre enn 1, og når er større enn 1, men hva skjer i 1?
Vi ser på definisjonen av den deriverte og ser hva som skjer hvis vi tar grensen ovenfra og nedenfra, altså at vi lar h gå mot null henholdsvis fra minussiden og plussiden. Husk definisjonen av den deriverte i et punkt :
Fra plussiden:
Vi ser at det her er som kommer i spill fordi er større enn 1.
Fra minussiden:
Vi ser at her kommer i spill fordi er mindre enn 1 ( er negativ.)
Som vi så på illustrasjonen får vi to forskjellige deriverte avhengig av hvilken side vi ser på. Da sier vi at grensen
ikke eksisterer, og funksjonen er ikke deriverbar.
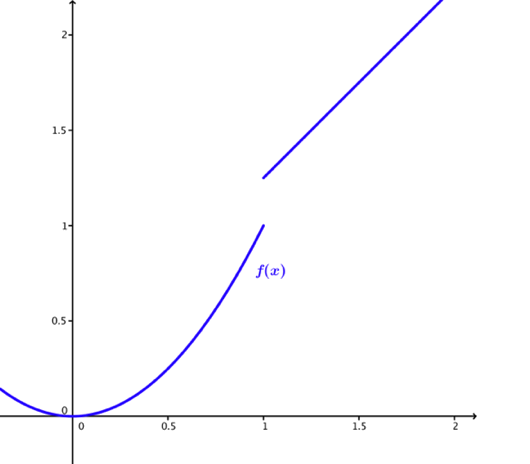
Eksempel 3 – en funksjon med et ikke-deriverbart punkt:
Under ser vi et eksempel på en funksjon som har et diskontinuerlig punkt; et punkt der den ikke henger sammen. Vi ser at i gjør den et hopp. Å finne stigningen i , gir ikke mening, og vi vet at ikke er deriverbar i 1.
Del på Facebook
Lynkurs 11.-13.trinn
Derivasjon
Består av:
- Introduksjon til derivasjon – gjennomsnittlig og momentan vekstfart
- Definisjon av den deriverte
- Deriverbarhet
- Derivasjonsregler
- Kjerneregelen
- Kjerneregelen - tre eksempler
- Derivasjon av sammensatte uttrykk
- Å finne tangenten - introduksjon
- Ettpunktsformelen og likning for tangentlinjen
- Høyere ordens deriverte
- Derivasjon av vektorfunksjoner 1 - Parameterframstilling
- Derivasjon av vektorfunksjoner 2 - vektorfunksjoner
- Derivasjon av vektorfunksjoner 3
Begrep
-
Kontinuerlig funksjon
En kontinuerlig funksjon er en sammenhengende graf, det vil si at grafen danner en sammenhengende kurve.