Øvingsoppgaver med fasit

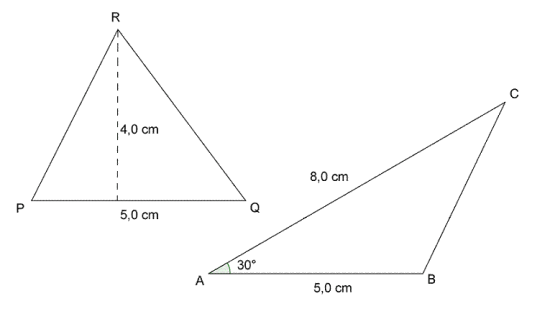
Hvilken av trekantene har størst areal?

I $\mathrm{\Delta }ABC$ er$\angle$A = 42,3°, AB = 12,3 cm og AC = 10,1 cm. Regn ut arealet av trekanten.

Finn arealet av $\mathrm{\Delta }$ABC når $\angle$A = 68°, $\angle$C = 22° og AB = 33,3

$\boxed{\text{?}}ABCD$ er et parallellogram der AB og DC er parallelle sider. $\angle A={60}^o$, AB = 8 dm og AD = 6 dm.

Finn arealet av parallellogrammet.

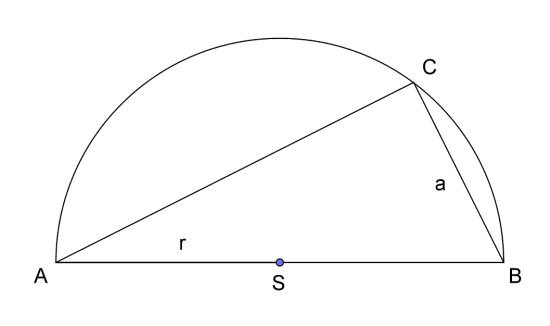
I en sirkel er periferivinkelen  ($\angle BCA$ ) alltid lik halve sentrumsvinkelen ( $\angle ASB$ ).

a) Forklar hvorfor $\mathrm{\Delta }ABC$ må være rettvinklet.

b) Anta at $BC=a$ og at $AC$ er dobbelt så lang som $BC$. Vis at arealet av halvsirkelen unntatt $\mathrm{\Delta }ABC$ er gitt ved $A=(\frac{5\pi }{8}-1)a^2$.

Finn arealet til $\mathrm{\Delta }$ABC når AB = 224 cm, AC = 132 cm og $\angle$A = 28,7°.

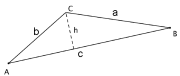
Bruk figuren til høyre og vis at $A_{\mathrm{\Delta }ABC}=\frac{bc\cdot \sin A}{2}$ 

I trekant ABC er AB = 3,2 cm, BC = 4,5 cm og vinkel B = 120^o.

Finn arealet av trekanten.

a) Konstruer en likesidet trekant ABC med sider 5 cm.

b) Roter trekanten 60 grader mot urviseren om B.

c) Hva heter den figuren du nå har fått?

d) Kall det siste hjørnet i den nye figuren for E og speil trekanten AEB om EB.

e) Hva heter den figuren du nå har fått?

f) Kall det siste hjørnet i den nye figuren for F og regn ut areal og omkrets av AEFC.

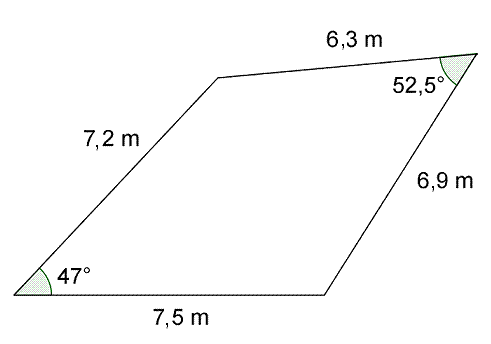
Hva er arealet av firkanten?