Øvingsoppgaver med fasit
Lenke til dette oppgavesettet (kan bokmerkes)Oppgaver
1
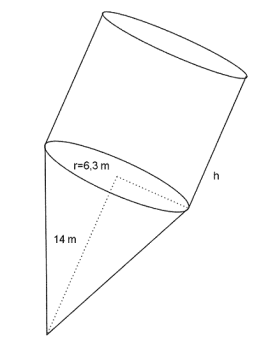
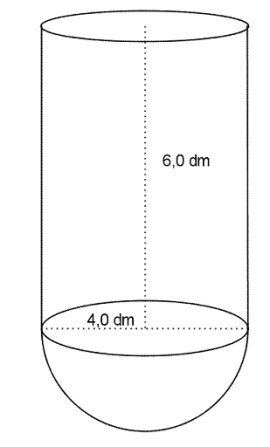
Volumet av figuren nedenfor er 2027 . Hva er høyden h til sylinderen?
2
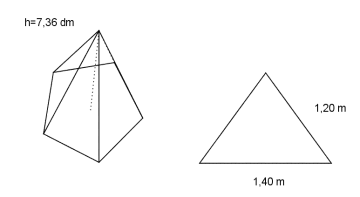
Nedenfor ser du en pyramide med en regulær femkant som grunnflate. Til høyre i figuren ser du et forstørret bilde av en av de fem likebeinte trekantene som til sammen utgjør femkanten.
Hva er volumet til pyramiden?
3
Anta du har en sylinder med radius r og høyde h og en kule med samme radius. Vi vil at de to objektene skal ha samme volum. Hva må da sammenhengen mellom r og h være? Finn en formel der du uttrykker r ved hjelp av h.
Hvis høyden er på 1,33 centimeter, hva er da radien?
4
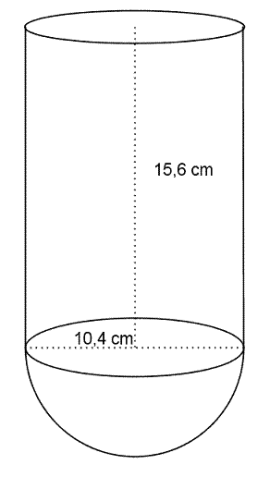
En kiste består av et rett, firkantet prisme og en halvsylinder. Halvsylinder ligger oppå prismet, og diameteren til sylinderen er lik bredden i prismet, mens høyden til sylinderen er lik lengden i prismet.
Anta at lengden til prismet er dobbelt så lang som bredden, og at høyden er lik bredden. Finn en formel for volumet V til kista, uttrykt ved høyden h til prismet (og ).
Hva blir volumet når høyden er 1 meter?
5
Finn volumet av figuren
6
Finn volumet av figuren
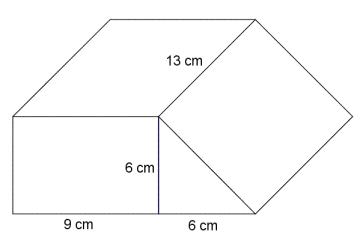
7
Finn volumet av figuren
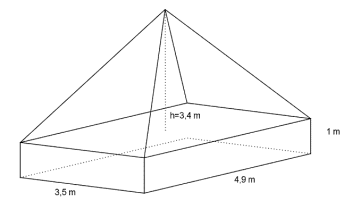
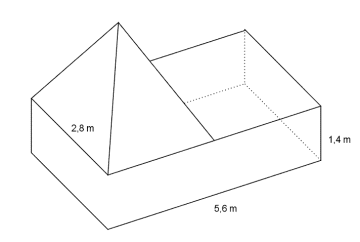
8
Finn volumet av figuren når du får oppgitt at høyden til pyramiden er 2,5 m.
9
Finn volumet av figuren
10
Hvor mye må radien i en kjegle endres for at volumet skal bli tre ganger så stort? (høyden holdes fast)
Gi et nøyaktig svar.
Fasit
1
h=11,6 m
2
Volumet er (ca.) 0,836
3
r=0,75h. Hvis høyden er som oppgitt vil radien være 1 cm.
4
Hvis høyden er 1 meter, blir volumet (ca.) 2,8 .
5
1618,9
6
36,6
7
936
8
28,5
9
92,1
10
Radien må økes med en faktor på