Prosent av hva da?
Husk at det alltid er prosent av noe. Her skal vi se hvor viktig det er å vite hva vi skal finne prosent (andelen) av.
Les disse to avisutklippene og legg godt merke til at prosenten ikke står alene.
|
|
|
|
Avinor skriver at utenlandstrafikken økte i juli med 14 prosent sammenlignet med samme måned i fjor. I utklippet under står det 61 prosent av brukerne. Hadde vi forstått hva Avinor mener hvis deres overskrift var "14 prosent i utlandstrafikken"? Nei, vi ville nok stilt spørsmålet om hva 14 prosent er av. Dette er eksempler som viser hvor viktig det alltid er å tenke på hva prosenten (andelen) er beregnet av.
La oss nå se på to typiske eksempler der mange gjør feil, fordi de ikke tenker på hva prosenten er beregnet av.
Eksempel 1. Minus , pluss
minus 50%, pluss 50%
av er .
Tar vi vekk av , får vi .
Men vi kommer IKKE tilbake til ved å legge til (av ) på !
av er , og vi får .
Vær nøye med hva som er opprinnelig verdi!
Eksempel 2. Prisen før salg
Mads var innom sportsforretningen og kjøpte en bordtennisracket til 68 kr. Alle prisene i butikken var allerede satt ned med 15%. Hvor mye kostet racketen før prisen ble satt ned?
Mads regnet på følgende måte:
68 kr + 15% av 68 kr .
Hvorfor er ikke dette riktig? Mads finner ut hva 15% av salgsprisen er og legger dette til den samme salgsprisen. Butikken har trukket fra 15% av den opprinnelige prisen og fått slagsprisen.Mads regnet ut feil verdi, fordi han ikke passet på hva han regnet prosent av. Nå skal vi vise hvordan vi finner den opprinnelige prisen på to måter.
Løsning 1. Opprinnelig verdi - Endring = Ny verdi
Ny verdi, salgsprisen: 68 kr,
Endring, avslag i pris: av "opprinnelig verdi"
Opprinnelig pris er ukjent.
Opprinnelig verdi:
Vi vet at den opprinnelige prisen minus av den opprinnelige prisen er lik salgsprisen. Dette setter vi opp som en likning:
.
Løser vi denne, får vi at .
Den opprinnelige prisen er 80 kr.
Løsning 2.
avslag betyr at slagsprisen er lik av den opprinnelige prisen. Da får vi
.
Del på Facebook
Begrep
-
Brøk
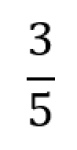
Brøk er et rasjonalt tall der teller og nevner er hele tall. Det er en måte å representere et tall på ved hjelp av divisjon. Nevneren må være forskjellig fra null.
Brøk kan sees som et tall på tallinja eller som del av en mengde.
-
Fellesnevner
Brøker med ulik nevner kan utvides slik at begge brøkene får samme nevner. Denne nevneren kalles fellesnevneren til brøkene.
Eksempel: , 42 er fellesnevner for disse to brøkene.
-
Ligning
En ligning er et åpent utsagn med en eller flere ukjent størrelser. Vi bruker som oftest x som den ukjente, men alle bokstaver kan brukes for å navngi den ukjente.
Eksempel:
-
Nevner
Tallet som står under brøkstreken i en brøk.
Nevneren forteller hvor mange like deler det hele er delt opp i.Eksempel : . Tallet 7 er nevneren.
-
Prosent
Prosent betyr hundredel og skrives %.
Eksempel: Hvor mange prosent er 1 av 4? .
-
Teller
Tallet eller uttrykket som står over brøkstreken i en brøk.
Telleren forteller hvor mange brøkdeler som skal telles med.
Eksempel: I brøken , er det 5 som er telleren. 9 kalles nevner.






