Multiplikasjon og divisjon av brøk

Oppbygging av undervisningsopplegget

• En kort introduksjon.
• Gjennomgå i plenum eksemplet som følger.
• Del ut oppgavearket til elevene.
• Introduser oppgave 1 og løs det i plenum.
• La elevene først jobbe individuelt med neste oppgave. Deretter diskuterer de løsningene i par og løser hverandres oppgaver.
• La elevene presentere løsningen i plenum og utfordre dem til å forklare denne før hele prosessen gjentas med neste oppgave.

Her finner du alle oppgavene sammen med kommentarene og ulike spørsmål som kan stilles til elevene. Oppgavene til elevene er i fanen "Elevens oppgaveark", mens løsningsforslaget er i høyre spalte under "Vedlegg".

Introduksjon:

• Hvilke oppgaver, eller "regnefortellinger", kan vi lage til brøkuttrykk?
• Hvordan kan vi illustrere med tegninger?
• Hva menes med delingsdivisjon og målingsdivisjon?

La oss se på det siste spørsmålet først.

Eksempel:

To tredeler skal deles på seks. Uttrykket blir da $\frac{2}{3}:6$

En passende oppgave, eller "regnefortelling", kan være:

"To tredels pizza skal deles på seks personer (resten har den sultne Tjodrik spist opp). Hvor mye (hvor stor del) får hver av de seks av hele pizzaen?"

Regner vi ut, finner vi at hver får en nidels pizza. Merk at vi hadde to tredels pizza og svaret ble en nidels pizza. Vi fikk samme benevning i svaret som vi hadde i oppgaven. Dette er et eksempel på delingsdivisjon. Vi kan spørre: Hvor mye fikk hver - av det vi hadde?

Illustrer dette med en tegning. Vi gjør det ikke her eller i neste eksempel, fordi i løsningsforslaget under "Vedlegg" finnes løsningene til alle oppgavene, inkludert illustrasjonene.

Snur vi på uttrykket foran, får vi $6:\frac{2}{3}$

Her er det vanskelig å lage en tilsvarende oppgave/"regnefortelling" som ovenfor.

Vi kunne sagt at: "Det går med seks kg gressfrø for å så inn to tredeler av plenen. Hvor mye trengs til hele plenen?" (Da ville vi hatt nok et eksempel på delingsdivisjon.)

Vi stiller i stedet spørsmålet slik: "Vi har seks kg sukker. Det skal legges i poser som hver tar to tredels kg. Hvor mange poser blir det?"

Det viser seg at de fleste elever synes den siste tilnærmingsmåten er enklest å forholde seg til. Her blir svaret 9 poser. Merk at her har vi 6 kg sukker. I svaret fikk vi 9 poser. Vi spurte om hvor mange. Vi får altså ikke samme benevning som vi hadde i utgangspunktet. Dette er et eksempel på målingsdivisjon. Vi måler opp hvor mange det blir.

Også her kan du godt illustrere med en tegning.

Først ser vi på multiplikasjon der brøkuttrykk inngår. Elevene kjenner til regelen

$\frac{\text{telller}\cdot \text{teller}}{\text{nevner}\cdot \text{nevner}}$

Er denne logisk? For at elevene skal forstå regelen godt nok, er det fint med en oppgave relatert til en virkelighet elever kan kjenne seg igjen i.

Oppgave 1.

$\frac{1}{3}\cdot \frac{1}{2}$

Løsningsforslag:

Regnefortelling: Du får tredjeparten av en halv sjokolade. Hvor mye får du av hele sjokoladen?
(Det blir det samme om du får tredjeparten av en halv sjokolade.)

Illustrasjon:

Her er sjokoladeplata:		Vi deler sjokoladeplata i to:
Også deler vi den ene halvparten i tre:		Da ser vi at en tredel av halvparten blir:
		en sjettedel ($\frac{1}{6}$) av hele plata

Og $\frac{1}{6}$ er selvsagt det samme som vi får hvis vi bruker regneregelen "direkte".

Oppgave 2.

Forklar geometrisk (ved tegning) hvorfor $2\frac{1}{2}\cdot \frac{1}{3}$ eller  $\frac{1}{3}\cdot 2\frac{1}{2}$ blir $\frac{5}{6}$

Hva med en passende regneoppgave til disse uttrykkene?

Løsningsforslag:

Regnefortelling:
Du får en tredel av to en halv liter brus. Hvor mye brus får du? Merk at oppgaven også kunne vært: To og en halv liter brus skal deles på tre personer. Hvor mye får hver? Oppstillingen på den siste blir $2\frac{1}{2}:3$ som tilsvarer $2\frac{1}{2}\cdot \frac{1}{3}$ og kan være en illustrasjon på sammenhengen mellom multiplikasjon og divisjon.

Illustrasjon:
Vi fremstiller de to og en halv liter brus ved å dele både litrene og halvliteren i tre like store deler. Den grå delen er hvor mye "vi får". Hver av tredelene er grå - for å markere at en tredel er det samme som to seksdeler:

Altså får vi fem seksdelsliter.

Oppgave 3.

Hva blir $\frac{2}{3}:4?$ Lag en regneoppgave.

Er dette delings- eller målingsdivisjon (ut fra regneoppgaven)?

Hvordan kan dette vises med tegning?

Løsningsforslag:

Regnefortelling:
To tredeler av et eple deles på fire. Hvor stor del av hele eplet får hver?

Illustrasjon:

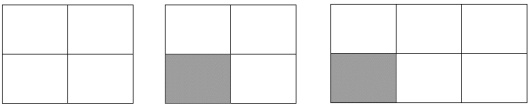
Her er hele:				Og her er $\frac{2}{3}$ av hele:
Vi deler de $\frac{2}{3}$ i 4:		Vi tar ut en "bit":		Og ser at vi får $\frac{1}{6}$ av det hele:

Vi kan selvsagt skrive $\frac{2}{3}:4=\frac{2}{3}:\frac{4}{1}=\frac{2}{3}\cdot \frac{1}{4}=\frac{2\cdot 1}{3\cdot 4}=\frac{2}{12}=\frac{1}{6}$

Men dette er kanskje ikke spesielt lett å forklare for elever som skal starte med brøk?

Hvorfor "snur vi" egentlig den siste brøken? Og må det nødvendigvis være den siste? Bør vi innpode en huskeregel i elevene - eller kan vi skape forståelse slik at de "finner logikken"?

Et relevant spørsmål: Var det en "tilfeldighet" at oppgave 1 og 3 ga samme svar?

(Tips: Hva om den siste oppgaven hadde vært $\frac{1}{3}:2$ eller om den første hadde vært $\frac{2}{3}\cdot \frac{1}{4}$?)

Oppgave 4.

Vi tenker oss at vi har ei kanne med 7 liter sagt, som skal fordeles på flasker som hver tar $\frac{1}{3}$ liter. Hvor mange flasker blir det?

Er dette delings- eller målingsdivisjon? Hva skiller målings- og delingsdivisjon?

Var den grei å ta "i hodet"? Hvordan tenkte du?

Hvilke spørsmål er det naturlig å stille for å finne det ut? Hva med benevning?

Løsningsforslag:

Slik oppgaven er stilt, er dette målingsdivisjon. Vi skal finne hvor mange flasker det blir, og svaret får altså ikke benevningen liter (som det ville blitt ved delingsdivisjon).

Det er ikke sikkert at alle elever (kanskje ganske få av dem som ikke har holdt mye på med brøkregning/-tenkning) vil finne svaret uten en tegning.

Illustrasjon:
Lag en tegning der du illustrerer de 7 literne som enheter - altså i enlitere.

Vi skulle ha flasker som hver tar $\frac{1}{3}$ liter. Så hvis vi deler hver av literne i tredels liter - hvor mange flasker får vi da? (For elever kan vi jo starte med å spørre hvor mange tredels liter - altså flasker - hver av literne gir.)

Nedenfor er hver liter delt i tre, dermed blir hver del en tredels liter. Så kan vi telle opp. og vis er at vi får 21 flasker. Vi kan også se det på en annen måte. Hver liter gir tre flasker. Vi har syv liter og da må vi multiplisere tre med syv. Da ser vi også enkelt hvorfor vi "snur den siste brøken", altså multipliserer med den omvendte brøken. I hvert fall når det gjelder stambrøker, men det kan sikkert utvides etter hvert.

For å løse oppgaven kan vi selvsagt skrive: $7:\frac{1}{3}=\frac{7}{1}:\frac{1}{3}=\frac{7}{1}\cdot \frac{3}{1}=\frac{21}{1}=21$

Oppgave 5.

a) $\frac{1}{2}:\frac{1}{4}=$

b) $\frac{2}{3}:\frac{1}{6}=$

Lag regneoppgaver. Vis løsningene geometrisk. Delings- eller målingsdivisjon?

Løsningsforslag 5 a):

Regnefortelling:
Et halvt tonn gjødsel er nok til (å fordele på) en kvart åker. Hvor mange tonn trengs til hele åkeren?

Eller

En halv liter lakk rekker til fjerdeparten av gulvet. Hvor mye trengs til å lakke hele gulvet?

Begge disse regnefortellingene oppleves som "kunstige". Her kan vi med fordel tenke målingsdivisjon og dette gir oss større mulighet for at de fleste elevene er med oss.

En halv liter saft skal helles i glass som tar en kvart liter. Hvor mange glass blir det?

Illustrasjon:

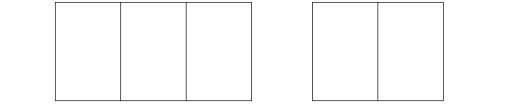
Her er en hel liter:		og her en halv:		som vi deler i to:

Så dersom vi deler en halv liter i glass som hvert tar en kvart liter, får vi to glass.

Løsningsforslag 5 b):

Regnefortelling:
Vi har to tredels liter brus. Rundt oss sitter forventningsfulle venner med hvert sitt glass som tar en seksdels liter. Hvor mange får?

Illustrasjon:

Her er en liter:		Her er det to tredels liter igjen.		Vi deler i seksdels litre:

Etter at vi har delt i seksdels litre, ser vi at de to tredelene gir fire enheter på en seksdels liter. (Den siste delingen kunne vi også ha gjort direkte fra figuren i midten, siden vi vet at en seksdel er halvparten av en tredel.)

Altså får fire av vennene våre fylt glasset sitt.

Den følgende er kanskje et lite hakk vanskeligere:

Oppgave 6.

$3\frac{1}{2}:1\frac{1}{6}$

Hva er en passende regneoppgave her? Og hvordan kan løsningen vises ved tegning?

Er regneoppgaven basert på målings- eller delingsdivisjon?

Løsningsforslag:

Regnefortelling:
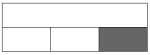
Vi har tre og en halv kg av ”noe” som skal fylles i poser som hver tar en og en seksdels kg. Hvor mange poser blir det?

Noen vil kanskje ”se” løsningen direkte. Tre seksdeler er jo lik en halv, altså er en halv delt på en seksdel lik tre – og deler vi tre på en, får vi også tre, så det blir altså tre poser. Dette resonnementet var kanskje ikke helt greit å følge (for mange elever), så det er sikkert lurt å lage figurer.

Illustrasjon:

Her er det tre og en halv kg representert:

Så kan vi dele opp i "biter" á seksdels kg. Siden vi vet at $1\frac{1}{6}$ er det samme som $\frac{7}{6}$, trenger vi syv av seksdelene til hver pose.

Og her kan vi "telle til syv" tre ganger, så vi får fylt akkurat tre poser.

 

Alle oppgavne til nå "gikk opp".

Men her kommer en som ikke gjør det:

Oppgave 7.

$3\frac{1}{2}:\frac{1}{3}$

Du kan sikkert regne den ut ved hjelp av brøkreglene (gjør gjerne det). Men lag uansett en regneoppgave og en tegning - og vis løsningen ut fra det.

Løsningsforslag:

Regnefortelling:
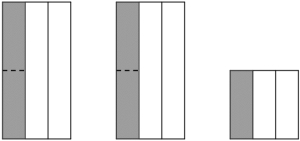
Jeg har funnet tre og en halv kilo gull som jeg vil smelte om til gullbarrer på en tredels kilo.

Noen vil sikkert se at tre hele kg vil gi ni barrer, siden hver kg gir tre. Og dermed gir den siste halve kg en og en halv barre. Til sammen blir det altså ti og en halv gullbarre. (Hvor mye veier den halve?)

Mange elever som har jobbet mye med slike oppgavetyper, vil nok også etter hvert se de enkle løsningsmetodene – og kunne forklare dem for medelever – og lærer på en lettfattelig måte. Andre vil helt sikkert måtte ha (for eksempel) ei tegning å forholde seg til.

Illustrasjon:
Her er de tre og en halv kg illustrert – oppdelt i ”biter” på en tredels kg. Vi ser at av en halv kg får vi en barre og en halv til overs.

Ekstraspørsmål:
Hva ville resultatet blitt dersom gullbarrene skulle veie en seksdels kilo? Altså om brøkuttrykket hadde vært:

$3\frac{1}{2}:\frac{1}{6}$

Undervisningsopplegget er også publisert i Tangenten 1/2010. For mer informasjon se under "Eksterne lenker".