Øvingsoppgaver med fasit
Lenke til dette oppgavesettet (kan bokmerkes)Oppgaver
1
Silje fikk 20 000 i konfirmasjon som hun satte inn på sparekonto der renten er 6,5% per år. Hvor mye penger har Silje på kontoen etter 3 år?
2
Radiumisotopen har en halveringstid på 1620 år. Anta at du har gram ved tiden .
a) Forklar at antall gram du har igjen etter år er gitt ved .
b) Når er den opprinnelige mengden med redusert med 20% ?
c) Når er det bare 10% igjen av opprinnelig mengde ?
3
På 1990 - tallet var det 38 100 innbyggere i en by. Antallet innbyggere økte med 1 % hvert år etter 1990. Hvor mange innbyggere var det i byen i 1990? Hvor mange innbyggere er det i byen etter t år?
4
David har mobiltelefon og for x minutters samtale, er prisen i kroner gitt ved formelen . Hvor mye betaler David for en samtale som varer i 5 minutter? Hvor lang var siste samtalen hans når den kostet 6.77 kr?
5
Bjørn har investert 12 000 kr i et aksjefond der den årlige prosentvise økningen er 4,3%. Hvor lang tid tar det før summen har steget til 15 500 kr?
6
Terje kjøpte en terrengsykkel for 18 000 kr og han regner med at verdien minker med 300 kr pr måned. Finn en formel for verdien V av terrengsykkelen etter t måneder og regn ut hva verdien av sykkelen er om 2 år. Hvor lang tid går det før verdien av mopeden er halvert?
7
Når på dagen var temperaturen høyest? Hva var temperaturen da?
8
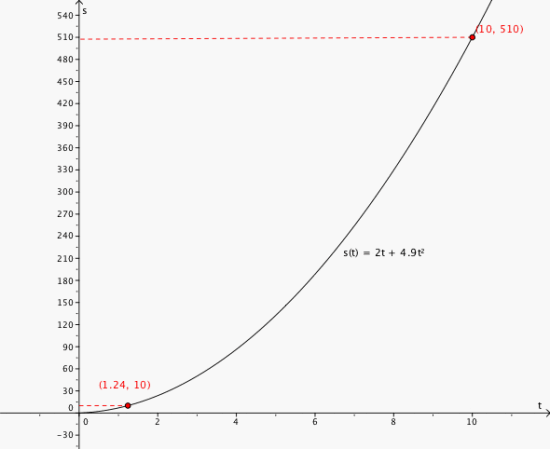
Fallstrekningen s meter etter t sekunder for en stein som blir kastet loddrett nedover, er gitt ved . Finn grafisk og ved regning hvor langt ned steinen har falt etter 10 sekunder og hvor lang tid det tar før steinen har falt 10 meter. Finn den momentane veksthastigheten når t = 5. Hva betyr dette?
9
En splitter ny datamaskin kostet 20 000 kr. Verdien avtar med 30% per år. Hvor mye er datamaskinen verdt etter t år?
10
Det årlige passasjertallet på en flyplass er på 985 000 med en antatt økning på 10% per år. På en annen flyplass er passasjertallet 2.5 millioner med en nedgang på 7% per år. Hvor lang tid går det før passasjerantallet er lik på de to flyplassene?
Fasit
1
24 159 kr
2
b) Etter år
c) Etter år
3
4
4.99 kr og 7 minutter
5
Ca. 6 år
6
, 10 800 kr og 2.5 år.
7
8
Steinen har falt ned 510 m etter 10 sekunder, mens det tar 1.24 sekunder før steinen har falt 10 meter. Den momentane veksthastigheten når t = 5 er 51 m/s i økning, det vil si farten øker.
9
10
5.5 år.