Øvingsoppgaver med fasit
Lenke til dette oppgavesettet (kan bokmerkes)Oppgaver
1
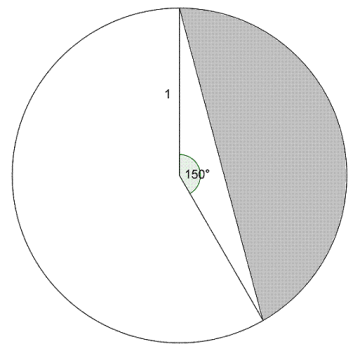
Radien i sirkelen er , og . Vis at arealet av det fargede området er gitt ved
.
2
I trekant PQR er PQ = 14, QR = 12 og PR= 8. Arealet av trekanten er 48. Finn B.
3
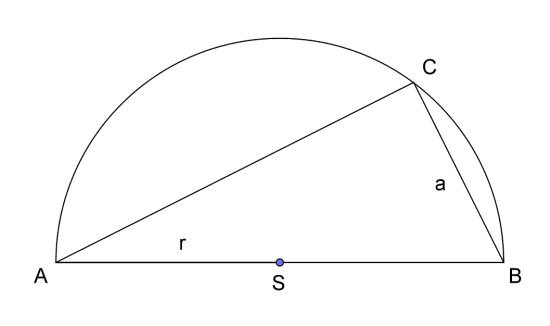
I en sirkel er periferivinkelen ( ) alltid lik halve sentrumsvinkelen ( ).
a) Forklar hvorfor må være rettvinklet.
b) Anta at og at er dobbelt så lang som . Vis at arealet av halvsirkelen unntatt er gitt ved .
4
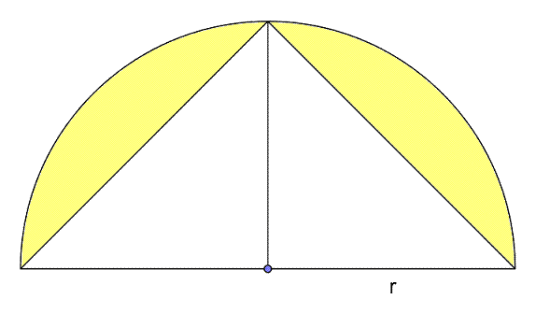
Vis at arealet av det fargede området kan skrives som
.
5
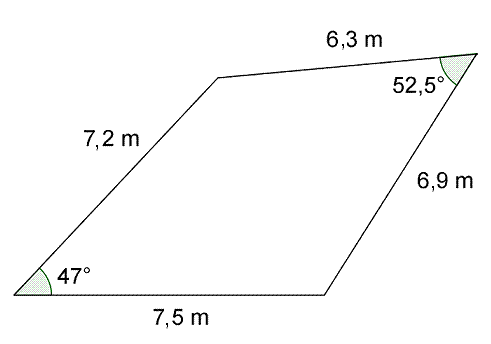
Hva er arealet av firkanten?
6
a) Konstruer en likesidet trekant ABC med sider 5 cm.
b) Roter trekanten 60 grader mot urviseren om B.
c) Hva heter den figuren du nå har fått?
d) Kall det siste hjørnet i den nye figuren for E og speil trekanten AEB om EB.
e) Hva heter den figuren du nå har fått?
f) Kall det siste hjørnet i den nye figuren for F og regn ut areal og omkrets av AEFC.
7
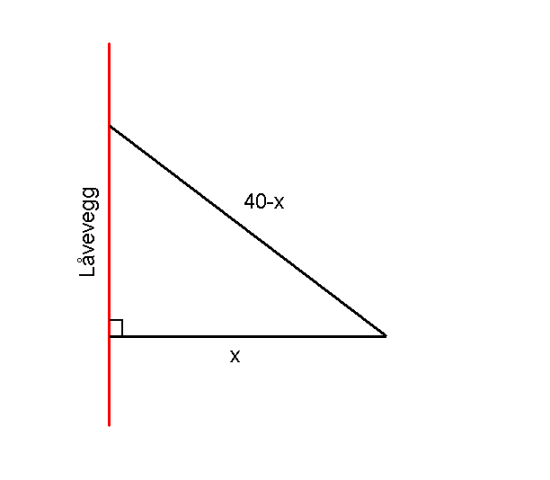
En bonde har m netting-gjerde og skal lage en innhegning for noen høns. Han bestemmer seg for å bruke låveveggen som den ene siden av innhegningen. På grunn av vanskelige grunnforhold med mye stein, ønsker han å bruke bare én påle, og dra nettingen rundt denne. Nettingen skal festes i veggen på to steder, og på det ene stedet, må gjerdet danne vinkel med låveveggen, se figur.
a) Vis at arealet av innhegningen er gitt ved .
b) Finn største mulige areal grafisk på lommeregneren.
8
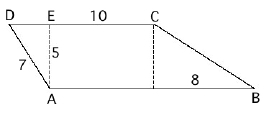
(CE = 10)
a) Hva heter figuren over? AB || CD
b) Regn ut omkrets og areal.
c) Konstruer figuren.
9
I erA = 42,3°, AB = 12,3 cm og AC = 10,1 cm. Regn ut arealet av trekanten.
10
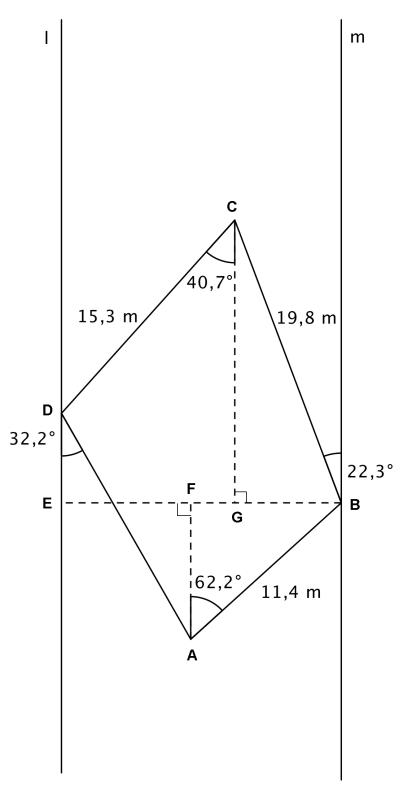
På figuren er linja l og m parallelle. Finn arealet av firkant ABCD.
Fasit
1
Hint: Arealet av sirkelsektoren minus arealet av trekanten.
2
B = 31°
3
a) Sentrumsvinkelen er , så .
b) Pytagoras' setning på gir . Følgelig blir arealet av halvsirkelen . Arealsetningen på trekanten gir at arealet av denne er .
4
Areal av farget område = areal av halvsirkel - areal av trekant
A =
5
37,0 m2
6
c) rombe
e) trapes
f) Arealet er ca 32,5 cm2 (høyde ca 4,33 cm). Omkretsen er 25 cm.
7
b)
8
a) Trapes
b) Omkrets ca 49,33 - Areal ca 82,25 (BC er ca 9,43 og ED ca 4,9)
9
41,8 cm2
10
214,0 m2